PQStat - Baza Wiedzy

Efekt podsumowujący

W wyniku działania meta-analizy najbardziej pożądanym jej elementem jest podsumowanie zebranych badań, czyli podanie wspólnego efektu 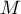$M$ . Takie podsumowanie może odbywać się na dwa sposoby, poprzez wyznaczenie efektu stałego lub efektu zmiennego.

Efekt stały

Wyliczając efekt stały zakładamy, że wszystkie badania w meta-analizie dzielą jeden wspólny prawdziwy efekt. Jeśli więc każde badanie dotyczyłoby tej samej populacji np. tego samego kraju, to chcąc podsumować meta-analizę efektem stałym zakładamy, że w każdym z tych badań prawdziwy (populacyjny) efekt będzie taki sam. Co za tym idzie, wszystkie czynniki, które mogłyby zaburzać wielkość tego efektu są takie same. Na przykład, jeśli na uzyskany efekt może wpływać wiek lub płeć badanych, to w każdym badaniu owe czynniki są podobne. Tak więc różnice w uzyskanych efektach dla poszczególnych badań wynikają tylko z błędu próbkowania (błędu wewnętrznego każdego badania) - czyli wielkości 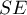$SE$ .

Efekt stały oszacowuje populacyjny efekt - prawdziwy efekt dla każdego z badań.

Przedział ufności wokół efektu stałego (szerokość rombu w wykresie leśnym) zależy tylko od poszczególnych 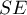$SE$ .

Efekt zmienny

Wyliczając efekt zmienny zakładamy, że każde badanie reprezentuje nieco inną populację, przez co prawdziwy (populacyjny) efekt będzie inny dla każdej populacji. Jeśli więc każde badanie dotyczyłoby innego kraju, to chcąc podsumować meta-analizę efektem zmiennym zakładamy, że niektóre czynniki, które mogłyby zaburzać wielkość tego efektu mogą mieć różne wielkości w poszczególnych krajach. Na przykład, jeśli na uzyskany efekt (np. średni wzrost dzietności) może wpływać poziom wykształcenia badanych czy zamożność danego kraju, a owe kraję różnią się tymi czynnikami, to w rezultacie prawdziwy efekt (średni wzrost dzietności) będzie nieco inny w każdym z tych krajów. Tak więc różnice w uzyskanych efektach dla poszczególnych badań wynikają z błędu próbkowania (błędu wewnątrz każdego badania) - czyli wielkości 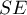$SE$ , oraz z różnic między badanymi populacjami (wariancji między badaniami - heterogeniczności badań) - czyli 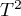$T^2$ . Owa heterogeniczność nie może być zbyt duża, zbyt duże zróżnicowanie pomiędzy badanymi populacjami wskazuje brak podstaw do wspólnego podsumowania.

Efekt zmienny oszacowuje średnią ważoną z prawdziwych (populacyjnych) efektów poszczególnych badań.

Przedział ufności wokół efektu zmiennego (szerokość rombu w wykresie leśnym) zależy od poszczególnych 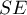$SE$ oraz od $T^2$ .

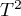Przedział ufności a przedział predykcji

95% przedział ufności (szerokość rombu w wykresie leśnym) - oznacza , że w 95% przypadkach takich meta-analiz podsumowujący efekt zmienny wpadnie do wyznaczonego przez romb przedziału.

95% przedział predykcji - oznacza, że w 95% przypadków prawdziwy (populacyjny) efekt nowego badania wpadnie do wyznaczonego przedziału.

Okno z ustawieniami opcji meta-analizy wywołujemy poprzez menu:

Statystyki zaawansowane→Meta-analiza→Podsumowanie.

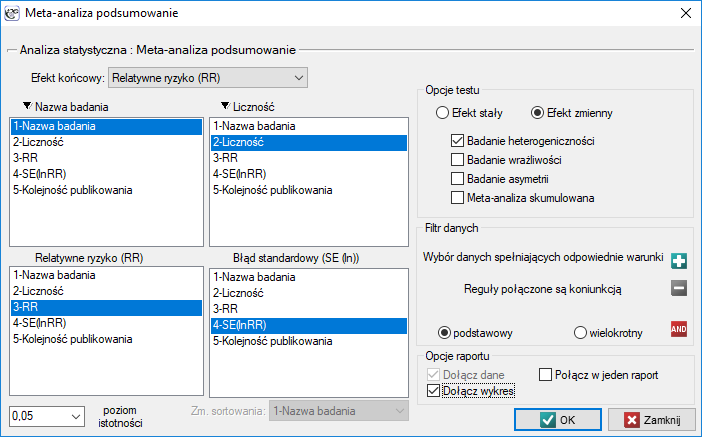
W oknie tym, w zależności od wybranego Efektu końcowego można dokonać podsumowania meta-analizy i przeprowadzić podstawowe analizy pozwalające na sprawdzenie jej założeń takich jak: heterogeniczność, błąd publikacyjny (badanie wrażliwości, asymetrii) oraz przeprowadzić meta-analizę skumulowaną.

Przykład (plik MetaanalizaRR.pqs)

Badano ryzyko choroby X dla osób palących i dla niepalących. W niektórych pracach naukowych wskazywano, że ryzyko wystąpienia choroby X jest większe dla palących, a w niektórych pracach nie udowodniono takiego związku. By ustalić czy palenie papierosów ma wpływa na występowanie choroby X zaplanowano przeprowadzenie meta-analizy. Wykonano dokładny przegląd literatury dotyczącej tego tematu i na tej podstawie wytypowano 10 prac naukowych do meta-analizy. Prace te dysponowały danymi, na podstawie których możliwe było wyliczenie relatywnego ryzyka (tzn. ryzyka zachorowania dla palących w stosunku do ryzyka zachorowania dla niepalących) i możliwe było ustalenie błędu jakim jest obciążone podane relatywne ryzyko (tzn. precyzji danego badania). Dane przygotowano do meta-analizy i zapisano w pliku.

Ze względu na to, że prace włączone do meta-analizy pochodziły z różnych ośrodków i obejmowały nieco inne populacje, podsumowania dokonano wybierając efekt zmienny. Jako efekt końcowy wybrano relatywne ryzyko oraz przedstawiono wyniki na wykresie leśnym.

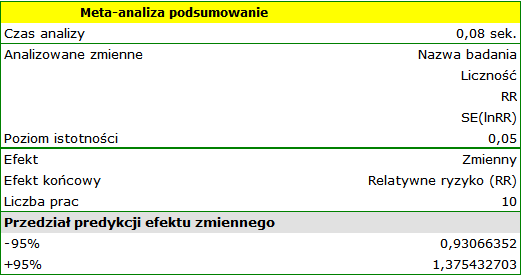
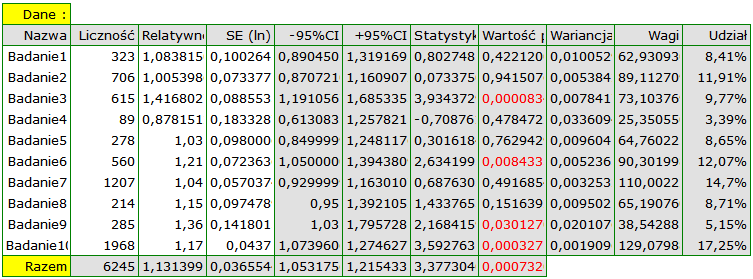
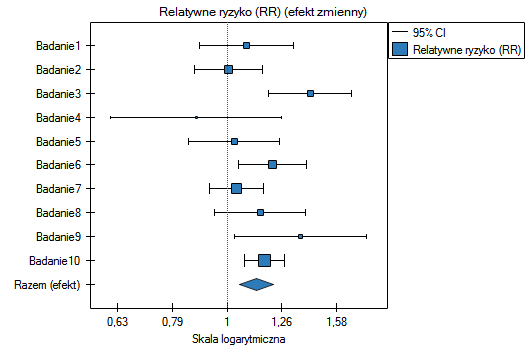
Wyniki czterech badań (badania 3, 6, 9 i 10) wskazują na istotnie wyższe ryzyko zachorowania dla palących. Wynik podsumowujący przeprowadzoną meta-analizę również jest istotny statystycznie i potwierdza ten sam efekt. Uzyskane relatywne ryzyko dla efektu podsumowującego wraz z 95% przedziałem ufności znajduje się powyżej wartości jeden: RR[95%CI]=1.13[1.05-1.22]. Niestety przedział predykcji efektu zmiennego jest szerszy: [0.93-1.38], co oznacza że w 95% przypadków prawdziwe, populacyjne relatywne ryzyko uzyskane w kolejnych badaniach, może być zarówno większe jak i mniejsze niż jeden.

Uwaga! Przed interpretacją wyników należy sprawdzić spełnienie założeń meta-analizy. W tym przypadku należy się zastanowić nad wykluczeniem badania trzeciego (patrz wyniki analizy wrażliwości, analizy asymetrii, meta-analizy skumulowanej oraz założenie heterogeniczności).

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Efekt podsumowujący

Narzędzia strony