PQStat - Baza Wiedzy

Badanie asymetrii

Symetria w uzyskanych efektach zwykle świadczy o braku obciążenia publikacyjnego, należy jednak pamiętać, że wiele obiektywnych czynników może zakłócić symetrię np. często nie są publikowane badania o nieistotnych statystycznie efektach lub badania małe, co znacznie utrudnia dotarcie do takich wyników. Jednocześnie brak jest dostatecznie wszechstronnych i uniwersalnych narzędzi statystycznych do detekcji asymetrii. W konsekwencji znaczna część przeprowadzanych meta-analiz publikowana jest mimo występującej zdiagnozowanej asymetrii. Badania takie wymagają jednakże dobrego uzasadnienia takiego postępowania.

Wykres lejkowy

$\begin{pspicture}(-1,-0.5)(7,5) \psline{->}(0,0)(0,4) \psline{->}(0,0)(5,0) \psdots(0.5,0.5) \psdots(1,1) \psdots(1.5,0.5) \psdots(1.5,2) \psdots(1.6,1.1) \psdots(1.8,2.4) \psdots(2,2) \psdots(2,2.8) \psdots(2.1,0.6) \psdots(2.5,4) \psdots(2.5,1.2) \psdots(2.5,2) \psdots(2.5,3) \psdots(2.5,4) \psdots(3,2.6) \psdots(2.8,3.1) \psdots(3,2) \psdots(2,1.3) \psdots(1.5,1.6) \psdots(3.3,2.2) \psellipse[linestyle=dashed,linecolor=red, dash=3pt 2pt](3.5,1)(-0.9,-0.9) \rput(3.5,1){\scriptsize bias} \rput(5.5,1.9){\scriptsize obciążenie publikacyjne} \rput(5.9,1.3){\scriptsize asymetryczny wykres} \rput(6.5,1.6){\tiny brak badań w prawym dolnym roku wykresu} \end{pspicture}$

Standardowym sposobem sprawdzenia obciążenia publikacyjnego w postaci asymetrii jest wykres lejkowy, pokazujący zależność pomiędzy wielkością badania (oś Y) a wielkością efektu podsumowującego (oś X). Zakłada się, że duże badania (umieszczone w górnej części wykresu) w prawidłowo dobranym zestawie, zlokalizowane są blisko siebie i wyznaczają środek leja, a badania mniejsze znajdują się niżej oraz są bardziej zróżnicowane i symetrycznie rozłożone. Zamiast wielkości badania na osi Y można przedstawić błąd efektu w danym badaniu, co jest lepszym rozwiązaniem niż przedstawienie samej wielkości badania. Błąd efektu jest bowiem miarą wskazującą na jakość badania i niosącą w sobie również informację o jego liczności.

Test Egger'a

Ponieważ interpretacja wykresu lejkowego jest zawsze subiektywna, pomocą może być wykorzystanie współczynnika Egger'a (Egger 1997¹⁾) - wyrazu wolnego w dopasowanej prostej regresji. Współczynnik ten bazuje na korelacji pomiędzy odwrotnością błędu standardowego i stosunkiem wielkości efektu do jego błędu. Czym bardziej oddalona od 0 wartość współczynnika, tym większa asymetria. Kierunek współczynnika określa rodzaj asymetrii: wartość dodatnia wraz z dodatnim przedziałem ufności dla niej wskazuje na zbyt wysoką wielkość efektu w małych badaniach a ujemna wraz z ujemnym przedziałem ufności na zbyt niską wielkość efektu w małych badaniach.

Uwaga! Test Egger'a powinien być używany tylko przy dużym zróżnicowaniu wielkości badań i występowaniu badania o średniej wielkości.

Uwaga! Przy niewielu badaniach (małej liczbie $k$ ) trudno jest osiągnąć istotny wynik mimo widocznej asymetrii.

Hipotezy:

$\begin{array}{cl} \mathcal{H}_0: & b = 0,\\ \mathcal{H}_1: & b \ne 0, \end{array}$

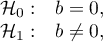
gdzie:

$b$ - to wyraz wolny w równaniu regresji Egger'a.

Statystyka testowa ma postać: $\begin{displaymath} t=\frac{b}{SE(b)} \end{displaymath}$

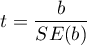
gdzie:

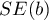$SE(b)$ - błąd standardowy wyrazu wolnego.

Statystyka testowa ma rozkład t-Studenta z 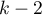$k-2$ stopniami swobody.

Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

Badanie liczby „Fail-safe”

Nfs Rosenthal’a - liczba „Fail-safe” opisana przez Rosenthal’a (1979²⁾) określa liczbę prac nie wskazujących na występowanie efektu (np. różnica średnich równa 0, iloraz szans równy 1 itp.) jaka jest potrzebna by zredukować efekt podsumowujący z istotnego statystycznie do statystycznie nieistotnego.

$\begin{displaymath} Nfs=\frac{\left(\sum_{i=1}^{k}Z_i\right)^2}{Z_c^2}-k \end{displaymath}$

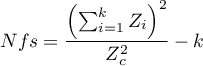
gdzie:

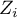$Z_i$ - wartość statystyki testowej (o rozkładzie normalnym) danego badania,

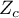$Z_c$ - wartość krytyczna rozkładu normalnego dla zadanego poziomu istotności,

$k$ - liczba badań w meta-analizie.

Rosenthal (1984) określił liczbę prac będącą punktem odcięcia jako 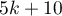$5k+10$ . Wyznaczając iloraz 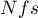$Nfs$ i punktu odcięcia uzyskujemy współczynnik(fs). Według interpretacji Rosenthal'a, jeśli współczynnik(fs) będzie większy niż 1, to prawdopodobieństwo obciążenia publikacyjnego jest minimalne.

Nfs Orwin’a - liczba „Fail-safe” opisana przez Orwin’a (1983³⁾) określa liczbę prac o średnim efekcie wskazanym przez badacza 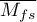$\overline{M_{fs}}$ , jaka jest potrzebna by zredukować efekt podsumowujący do pożądanej wielkości 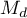$M_d$ wskazanej przez badacza.

$\begin{displaymath} Nfs=k\frac{M - M_d}{M_d-\overline{M_{fs}}} \end{displaymath}$

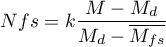
gdzie:

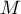$M$ - efekt podsumowujący uzyskany w meta-analizie.

Przykład c.d. (plik MetaanalizaRR.pqs)

Badając wpływ palenia papierosów na wystąpienie choroby X sprawdzono założenie dotyczące asymetrii badań, a więc obciążenia publikacyjnego. W tym celu w oknie analizy wybrano opcję Badanie asymetrii oraz wskazano wykres lejkowy.

Wynik testu Eggera nie są istotne statystycznie (p=0.9137), co wskazuje na brak obciążenia publikacyjnego.

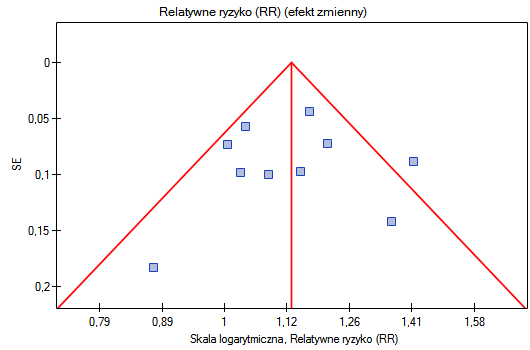
Punkty, przedstawiające poszczególne badania są rozłożone symetrycznie na wykresie lejkowym. Co prawda jedno badanie znajduje się poza obrębem trójkąta (Badanie 3), ale jest blisko jego brzegów. Na podstawie wykresu również nie mamy zasadniczych zastrzeżeń co do doboru badań, jedyna wątpliwość dotyczy badania trzeciego.

Liczba publikacji „Fail-safe” wyznaczona metodą Rosenthal'a jest duża i wynosi 72. Zatem, jeśli efekt podsumowujący (wspólne dla wszystkich badań relatywne ryzyko) miałby być nieistotny statystycznie (palenie papierosów miałoby nie wpływać na ryzyko choroby X), należałoby dołączyć do zebranych prac jeszcze 72 prace w których relatywne ryzyko wynosi jeden. Uzyskany efekt można więc uznać za stabilny, gdyż nie będzie można łatwo (niewielką liczbą prac) podważyć uzyskanego efektu.

Uzyskane, wspólne relatywne ryzyko wynosi RR=1.13. Wykorzystując metodę Orwin'a sprawdzono jak wiele prac o relatywnym ryzyku równym 1.11 potrzeba włączyć, by wspólne relatywne ryzyko spadło do wielkości 1.12. Uzyskany rezultat to 11 prac. Natomiast zmniejszając wielkość relatywnego ryzyka z 1.11 do 1.10 już tylko 5 prac potrzeba by wspólne relatywne ryzyko wyniosło 1.12.

¹⁾

Egger M., Smith G. D., Schneider M., Minder C (1997), Bias in meta-analysis detected by a simple, graphical test. BMJ, 315(7109):629-634

²⁾

Rosenthal R. (1979), The „file drawer problem” and tolerance for null results. Psychological Bulletin, 5, 638-641

³⁾

Orwin R. G. (1983), A Fail-SafeN for Effect Size in Meta-Analysis. J Educ Behav Stat, 8(2):157-159

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Badanie asymetrii

Narzędzia strony