Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:metapl:regresja
Spis treści
Meta-regresja
Analiza meta-regresji jest przeprowadzana w analogiczny sposób do analizy regresji opisanej w dziale Liniowa regresja wieloraka. W przypadku meta-regresji badanymi obiektami są poszczególne badania, ich wyniki (np. ilorazy szans, relatywne ryzyka, różnice średnich) stanowią zmienną zależną  czyli wyjaśnianą, natomiast dodatkowe warunki przeprowadzania tych badań stanowią zmienne niezależne (
czyli wyjaśnianą, natomiast dodatkowe warunki przeprowadzania tych badań stanowią zmienne niezależne ( ,
,  ,
,  ,
, 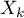 ) czyli wyjaśniające. Podobnie jak w tradycyjnych modelach regresji, zmienne niezależne mogą wchodzić w interakcje a te, które są opisane skalą nominalną mogą podlegać specjalnemu kodowaniu (więcej informacji na ten temat można znaleźć w rozdziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych). Liczba zmiennych niezależnych powinna być niewielka, mniejsza niż liczba prac na podstawie których przeprowadza się badanie (
) czyli wyjaśniające. Podobnie jak w tradycyjnych modelach regresji, zmienne niezależne mogą wchodzić w interakcje a te, które są opisane skalą nominalną mogą podlegać specjalnemu kodowaniu (więcej informacji na ten temat można znaleźć w rozdziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych). Liczba zmiennych niezależnych powinna być niewielka, mniejsza niż liczba prac na podstawie których przeprowadza się badanie (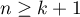 ).
).
Meta-regresję możemy przeprowadzić wybierając efekt stały lub efekt zmienny.
- Efekt stały wybieramy wtedy, gdy zakładamy, że badania przedstawiają jeden wspólny prawdziwy efekt w taki sposób, że wszystkie czynniki, które mogłyby zaburzać wielkość tego efektu są takie same, za wyjątkiem czynników badanych jako zmienne niezależne w modelu (
 ,
,  ,
,  ,
, 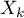 ). Jest to sytuacja występująca bardzo rzadko w prawdziwych badaniach, ponieważ wymaga w pełni kontrolowanych warunków, co w przypadku różnych badań, prowadzonych przez różne ośrodki i różnych badaczy jest prawie niemożliwe. Wykorzystanie efektu stałego miało by uzasadnienie na przykład w sytuacji, gdy wszystkie badania przeprowadza jeden ośrodek, na tej samej populacji, przy zmianie tylko tych warunków które opisuje badana cecha. Na przykład, jeśli chcielibyśmy sprawdzić jak wpływa zmiana temperatury na zmianę opisanej w poszczególnych badaniach wielkości relatywnego ryzyka występowania choroby, wówczas wszystkie badania powinny być przeprowadzone na tej samej populacji w dokładnie tych samych warunkach za wyjątkiem zmiany temperatury, która stanowi zmienną niezależną
). Jest to sytuacja występująca bardzo rzadko w prawdziwych badaniach, ponieważ wymaga w pełni kontrolowanych warunków, co w przypadku różnych badań, prowadzonych przez różne ośrodki i różnych badaczy jest prawie niemożliwe. Wykorzystanie efektu stałego miało by uzasadnienie na przykład w sytuacji, gdy wszystkie badania przeprowadza jeden ośrodek, na tej samej populacji, przy zmianie tylko tych warunków które opisuje badana cecha. Na przykład, jeśli chcielibyśmy sprawdzić jak wpływa zmiana temperatury na zmianę opisanej w poszczególnych badaniach wielkości relatywnego ryzyka występowania choroby, wówczas wszystkie badania powinny być przeprowadzone na tej samej populacji w dokładnie tych samych warunkach za wyjątkiem zmiany temperatury, która stanowi zmienną niezależną  w modelu.
w modelu. - Efekt zmienny wybieramy wtedy, gdy zakładamy, że badania mogą przedstawiać nieco różniące się populacje tzn. czynniki, które mogłyby zaburzać wielkość badanego efektu nie we wszystkich pracach są opisane (można założyć, że są podobne, ale nie muszą być dokładnie takie same). Każda praca podaje wielkości czynników, którymi jesteśmy zainteresowani, które biorą udział w budowaniu modelu jako zmienne niezależne (
 ,
,  ,
,  ,
, 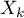 ). Wykorzystanie efektu zmiennego jest częste, ponieważ poszczególne badania przeprowadzane są najczęściej przez różne ośrodki w nieco innych warunkach, interesująca zmienność dotyczy tylko tych warunków które opisują podane w badaniu czynniki np. temperatura, która stanowić będzie zmienną niezależną
). Wykorzystanie efektu zmiennego jest częste, ponieważ poszczególne badania przeprowadzane są najczęściej przez różne ośrodki w nieco innych warunkach, interesująca zmienność dotyczy tylko tych warunków które opisują podane w badaniu czynniki np. temperatura, która stanowić będzie zmienną niezależną  w modelu.
w modelu.
Weryfikacja modelu
Istotność statystyczna poszczególnych zmiennych w modelu.
Na podstawie współczynnika oraz jego błędu możemy wnioskować czy zmienna niezależna, dla której ten współczynnik został oszacowany wywiera istotny wpływ na efekt końcowy. W tym celu testujemy hipotezy:
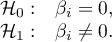
Wyliczmy statystykę testową według wzoru:
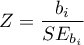 Statystyka testowa ma rozkład normalny.
Statystyka testowa ma rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności poziomem istotności
porównujemy z poziomem istotności poziomem istotności  :
:

Jakość zbudowanego modelu liniowej regresji wielorakiej możemy ocenić kilkoma miarami.
- Współczynnik R2 - jest miarą dopasowania modelu. Wyraża on procent zmienności pomiędzy efektami badań tłumaczony przez model.
Wartość tego współczynnika mieści się w przedziale 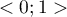 , gdzie 1 oznacza doskonałe dopasowanie modelu, 0 - zupełny bark dopasowania. W jego wyznaczeniu posługujemy się następującą równością:
, gdzie 1 oznacza doskonałe dopasowanie modelu, 0 - zupełny bark dopasowania. W jego wyznaczeniu posługujemy się następującą równością:
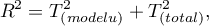
gdzie:
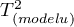 - wariancja między badaniami wyjaśniona przez model,
- wariancja między badaniami wyjaśniona przez model,
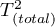 - całkowita wariancja między badaniami.
- całkowita wariancja między badaniami.
- Współczynnik I2 - określa procent obserwowanej wariancji, jaki wynika z rzeczywistej różnicy w wielkości badanych efektów.
Uwaga! Dokładne przedstawienie opisywanej przez współczynniki wariancji można znaleźć w dziale Badanie heterogeniczności
Istotność statystyczna wszystkich zmiennych w modelu
Podstawowym narzędziem szacującym istotność wszystkich zmiennych w modelu jest ANOVA wyznaczająca  (modelu).
(modelu).
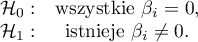
Wykorzystując podejście ANOVA, obserwowaną wariancję pomiędzy badaniami rozbija się na wariancję tłumaczoną przez model i wariancję reszt (nie tłumaczoną przez model). W rezultacie wyznaczone zostają następujące statystyki  :
:
- Statystyka
 (reszty) - bada tę część wariancji łącznej, która nie jest tłumaczona przez model,
(reszty) - bada tę część wariancji łącznej, która nie jest tłumaczona przez model, - Statystyka
 (modelu) - bada tę część wariancji łącznej, która jest tłumaczona przez model,
(modelu) - bada tę część wariancji łącznej, która jest tłumaczona przez model, - Statystyka
 (łączna) - bada wariancję pomiędzy wszystkimi badaniami.
(łączna) - bada wariancję pomiędzy wszystkimi badaniami.
Każda z powyższych statystyk  ma rozkład chi-kwadrat z odpowiednią dla niej liczbą stopni swobody.
ma rozkład chi-kwadrat z odpowiednią dla niej liczbą stopni swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności poziomem istotności
porównujemy z poziomem istotności poziomem istotności  :
:

Okno z ustawieniami opcji porównania grup dla meta-analizy wywołujemy poprzez menu: Statystyki zaawansowane→Meta-analiza→Porównanie grup.
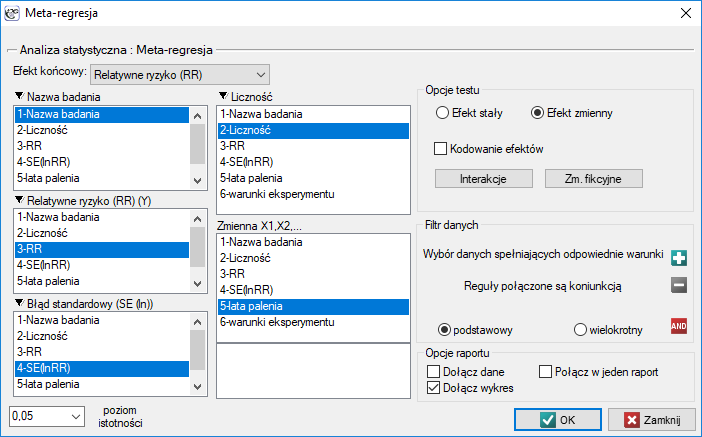
Przykład c.d. (plik MetaanalizaRR.pqs)
Badano ryzyko choroby X dla osób palących i dla niepalących. By ustalić czy czas pozostawania w nałogu ma wpływa na występowanie choroby X oraz czy różne warunki eksperymentu przełożyły się na różnice w uzyskanym relatywnym ryzyku, wykonano meta-analizę porównującą wyodrębnione grupy badań. Na podstawie porównania grup badań udało się ustalić, że ostatnia grupa (grupa palących najdłużej, tzn. dłużej niż 10 lat) wskazuje na związek pomiędzy paleniem a występowaniem choroby X. Natomiast dla grup, w których czas palenia był krótszy, nie udało się uzyskać istotnego efektu. Zauważono jednak, że efekt systematycznie rośnie wraz z upływem lat palenia. By sprawdzić hipotezę o istotnym zwiększeniu ryzyka choroby X wraz z upływem lat palenia papierosów zbudowano dwa modele regresji. W pierwszym modelu zmienną grupującą Lata palenia potraktowano jak zmienną ciągłą. W modelu drugim ustalono, że zmienna Lata palenia traktowana będzie jako zmienna kategorialna (fikcyjna) z grupą odniesienia palącą krócej niż 5 lat. Dane przygotowano do meta-analizy i zapisano w pliku.
Ze względu na to, że prace włączone do meta-analizy pochodziły z różnych ośrodków i obejmowały nieco inne populacje, meta-regresję wykonano wybierając efekt zmienny. Jako efekt końcowy wybrano relatywne ryzyko oraz przedstawiono wyniki na wykresie.

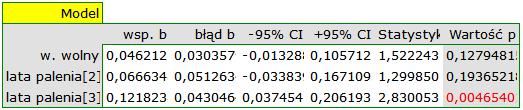
W obu modelach potwierdzono istotny związek pomiędzy czasem palenia a wielkością relatywnego ryzyka wystąpienia choroby X. W modelu pierwszym ustalono, że wraz ze upływem czasu palenia (przejściem do kolejnej grupy lat palenia) logarytm relatywnego ryzyka choroby X zwiększy się o 0.06139. Do podobnych wniosków prowadzi analiza wyników modelu drugiego. W tym przypadku wyniki rozpatrujemy w odniesieniu do grupy palących krócej niż 5 lat. Logarytm relatywnego ryzyka dla palących od 5 do 10 lat wzrasta o 0.06663 (w stosunku do palących krócej niż 5 lat), a dla palących dłużej niż dziesięć lat wzrasta aż o 0.12182 (w stosunku do palących krócej niż 5 lat).
Ponieważ część badań prowadzona była według innych kryteriów (w innych warunkach) uzyskane wyniki obu modeli skorygowano różne warunki prowadzenia badań.

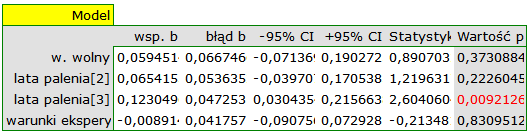
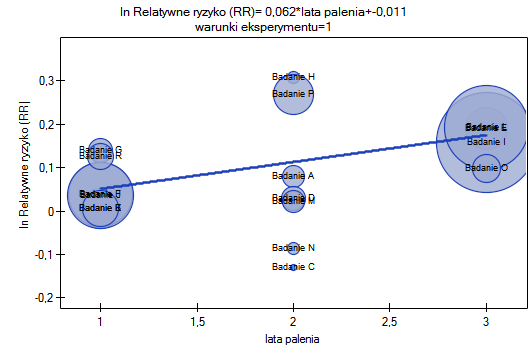
Przeprowadzona korekcja nie zmieniła zasadniczej tendencji, a więc można uznać, że ryzyko wystąpienia choroby X wzrasta wraz z upływem lat palenia bez względu na to jaką metodologię (kryteria włączenia/wyłączenia osób) stosowano by przeprowadzić badania. Uzyskaną zależność dla modelu pierwszego, przy założeniu prowadzenia badań w warunkach „a” (wskazanych jako warunki pierwsze) przedstawia wykres.
2018/03/04 11:59
· admin
statpqpl/metapl/regresja.txt · ostatnio zmienione: 2018/03/04 13:01 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


