Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:metapl:porownanie
Spis treści
Porównanie grup
Bywają sytuacje, w których zebrane dane dotyczą tego samego efektu, są wykonywane na tej samej populacji, ale w nieco innych warunkach. Załóżmy że część badań była przeprowadzona w warunkach A, a część w warunkach B. Wówczas interesujące może być porównanie uzyskanych dla każdej grupy efektów podsumowujących. Wykazanie różnic pomiędzy efektami podsumowującymi może być głównym celem meta-analizy i wówczas niewskazane jest podsumowanie jednym wspólnym efektem obu podgrup jednocześnie. Jeśli jednak badacz zdaje sobie sprawę że badania przeprowadzane były w różnych warunkach, ale celowe wydaje się wspólne podsumowanie wszystkich badań, wówczas wykazując brak istotnych statystycznie (lub klinicznie) różnic, może dokonać wspólnego podsumowania uwzględniając jednocześnie ów podział na podgrupy A i B, czyli wyznaczyć wspólne podsumowanie w korekcji o różne warunki eksperymentu. Np. W kraju A panuje nieco inny klimat niż w kraju B. Dysponujemy szeregiem badań dotyczących kraju A i szeregiem badań dotyczących kraju B. Jeśli naszą populacją badaną jest roślinność tych dwóch krajów, to możemy sprawdzić, czy warunki klimatyczne mają wpływ na uzyskane efekty badań dla poszczególnych krajów. Analiza porównawcza wyznaczonych w ten sposób podgrup pozwoli ocenić czy klimat ma zasadniczy wpływ na uzyskiwane wyniki, czy też nie i czy można rzeczywiście wyniki badań obejmujące te dwa kraje podsumować jednym wspólnym efektem, czy też powinniśmy wyznaczać oddzielne podsumowania dla każdego kraju. Innym przykładem może być sytuacja, gdy część badań to badania, w których przeprowadzona była randomizacja ale w części nie mamy pełnej randomizacji, wówczas możemy podzielić badania na podgrupy, by następnie sprawdzić czy badania bez randomizacji dają na tyle zbliżone efekty do badań z randomizacją by móc je włączyć do dalszej, wspólnej analizy.
Heterogeniczność grup
Badanie heterogeniczności grup
Porównania grup możemy dokonać wybierając jako efekt podsumowujący: efekt stały, efekt zmienny - oddzielne 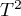 lub efekt zmienny - wspólne
lub efekt zmienny - wspólne 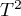 , gdzie
, gdzie 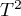 to wariancja obserwowanych efektów.
to wariancja obserwowanych efektów.
- Efekt stały wybieramy wtedy, gdy zakładamy, że badania wewnątrz każdej grupy dzielą jeden wspólny prawdziwy (tzn. populacyjny) efekt.
- Efekt zmienny (oddzielne T2) wybieramy wtedy, gdy zakładamy że badania wewnątrz każdej grupy reprezentują nieco inne populacje, oraz grupy różnią się wariancją pomiędzy badaniami.
- Efekt zmienny (wspólne T2) wybieramy wtedy, gdy zakładamy że badania wewnątrz każdej grupy reprezentują nieco inne populacje, ale wariancja pomiędzy badaniami jest taka sama, bez względu na grupę do której przynależą.
W rezultacie każda grupa zostaje opisana oddzielnie wybranym efektem podsumowującym.
Celem głównym jest porównanie grup, czyli ustalenie, czy porównywane grupy różnią się prawdziwym (tzn. populacyjnym) efektem podsumowującym. W praktyce jest to sprawdzenie czy wariancja efektów podsumowujących grupy jest zerowa, czyli badanie heterogeniczności grup. Opis i interpretacja wyników analizy heterogeniczności znajduje się w rozdziale Badanie heterogeniczności, z tym że w przypadku porównania grup heterogeniczność dotyczy efektów podsumowujących porównywanych grup, nie poszczególnych badań, a wynik uzależniony jest od wybranego efektu podsumowującego.
Hipotezy:
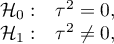
gdzie:
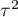 - to wariancja prawdziwych (populacyjnych) efektów podsumowujących porównywanych grup.
- to wariancja prawdziwych (populacyjnych) efektów podsumowujących porównywanych grup.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Jeśli uzyskamy wynik jest istotny statystycznie (wynik statystyki Q, współczynnika I2 lub współczynnika H2), jest to mocna sugestia, by zrezygnować z wspólnego podsumowywania porównywanych grup.
Badanie heterogeniczności w grupach
Dodatkową opcją analizy jest możliwość przeanalizowania każdej grupy oddzielnie pod kątem heterogeniczności, zgodnie z opisem w rozdziale Badanie heterogeniczności. Uzyskane wyniki (w szczególności wyznaczona wariancja T2) ułatwiają podjęcie decyzji co do sposobu porównania grup tzn. wyboru efektu zmiennego (oddzielne 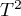 ) lub efektu zmiennego (wspólne
) lub efektu zmiennego (wspólne 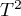 ).
).
Wspólne podsumowanie grup
W sytuacji, w której na podstawie wyników porównania grup, różnice uzyskane pomiędzy efektami podsumowującymi poszczególne grupy są niewielkie i nieistotne, można dokonać wspólnego podsumowania tych grup. Podsumowanie odbywa się w korekcji o podział na wskazane grupy. Jeśli na przykład badania dzieliliśmy na podstawie różnych warunków prowadzonego eksperymentu, wówczas wspólne podsumowanie dokonane zostanie w korekcji o różne warunki eksperymentu. Rezultat wspólnego podsumowania zależy od obserwowanych różnic (od wariacji pomiędzy badaniami i pomiędzy grupami) czyli od wyboru efektu podsumowującego (czy jest to efekt stały, czy zmienny (oddzielne 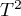 ), czy też zmienny (wspólne
), czy też zmienny (wspólne 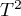 )).
)).
Dobrym zilustrowaniem wspólnego podsumowania grup w meta-analizie jest wykres leśny przedstawiający wyniki poszczególnych badań wraz z podsumowaniem każdej grupy i wspólnym podsumowaniem grup.
Porównanie ANOVA
Porównanie ANOVA jest dodatkową opcją porównania grup, jest to nieco inna metoda porównania niż porównanie poprzez badanie heterogeniczności grup (oparta na innym modelu matematycznym). Obie metody dają jednakże zbieżne wyniki, co do porównania grup. W przypadku porównania grup metodą ANOVA obserwowana wariancja zostaje rozbita na wariancję między grupami i wariancję wewnątrz grup. Wariancja wewnątrz grup rozbita zostaje następnie na wariancję każdej grupy oddzielnie. W rezultacie wyznaczone zostają następujące statystyki  :
:
- Statystyka
 (grupa 1) - bada tę część wariancji łącznej, która odnosi się do grupy pierwszej, czyli wariancję pomiędzy badaniami znajdującymi się wewnątrz grupy pierwszej,
(grupa 1) - bada tę część wariancji łącznej, która odnosi się do grupy pierwszej, czyli wariancję pomiędzy badaniami znajdującymi się wewnątrz grupy pierwszej, - Statystyka
 (grupa 2) - bada tę część wariancji łącznej, która odnosi się do grupy drugiej, czyli wariancję pomiędzy badaniami znajdującymi się wewnątrz grupy drugiej,
(grupa 2) - bada tę część wariancji łącznej, która odnosi się do grupy drugiej, czyli wariancję pomiędzy badaniami znajdującymi się wewnątrz grupy drugiej, - …
- Statystyka
 (grupa g) - bada tę część wariancji łącznej, która odnosi się do grupy ostatniej, czyli wariancję pomiędzy badaniami znajdującymi się wewnątrz grupy ostatniej,
(grupa g) - bada tę część wariancji łącznej, która odnosi się do grupy ostatniej, czyli wariancję pomiędzy badaniami znajdującymi się wewnątrz grupy ostatniej, - Statystyka Q(wewnątrz grup) =
 (grupa 1) +
(grupa 1) +  (grupa 2) + … +
(grupa 2) + … +  (grupa g) - bada tę część wariancji łącznej, która odnosi się do wnętrza poszczególnych grup, czyli wariancję badań wewnątrz poszczególnych grup,
(grupa g) - bada tę część wariancji łącznej, która odnosi się do wnętrza poszczególnych grup, czyli wariancję badań wewnątrz poszczególnych grup, - Statystyka
 (między grupami) - bada tę część wariancji łącznej, która odnosi się do różnic między grupami, czyli wariancję pomiędzy grupami (wynik tożsamy z badaniem heterogeniczności grup) ,
(między grupami) - bada tę część wariancji łącznej, która odnosi się do różnic między grupami, czyli wariancję pomiędzy grupami (wynik tożsamy z badaniem heterogeniczności grup) , - Statystyka
 (łączna) - bada wariancję pomiędzy wszystkimi badaniami.
(łączna) - bada wariancję pomiędzy wszystkimi badaniami.
Każda z powyższych statystyk  ma rozkład chi-kwadrat z odpowiednią dla niej liczbą stopni swobody.
ma rozkład chi-kwadrat z odpowiednią dla niej liczbą stopni swobody.
Okno z ustawieniami opcji porównania grup dla meta-analizy wywołujemy poprzez menu: Statystyki zaawansowane→Meta-analiza→Porównanie grup.
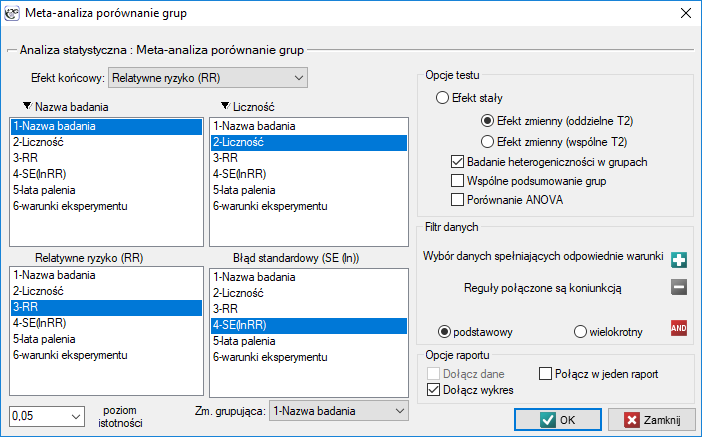
Przykład (plik MetaanalizaRR.pqs)
Badano ryzyko choroby X dla osób palących i dla niepalących. By ustalić czy czas pozostawania w nałogu ma wpływa na występowanie choroby X zaplanowano przeprowadzenie meta-analizy. Wykonano dokładny przegląd literatury dotyczącej tego tematu i na tej podstawie wytypowano 17 prac naukowych dysponujących opisem relatywnego ryzyka i jego błędu (tzn. precyzji danego badania). Ze względu na to, że badania dotyczyły różnego czasu palenia, wyodrębniono 3 grupy badań:
(1) badania dotyczące palących dłużej niż 10 lat,
(2) badania dotyczące palących od 5 do 10 lat,
(3) badania dotyczące palących krócej niż 5 lat.
Dodatkowo dokonano podziału na dwa różne warunki przeprowadzanych badań (różne kryteria włączenia/wyłączenia osób). Dane przygotowano do meta-analizy i zapisano w pliku.
Celem przeprowadzania meta-analizy było porównanie grup wiekowych. Dodatkowo sprawdzono, czy różne warunki eksperymentu przełożyły się na różnice w uzyskanym relatywnym ryzyku.
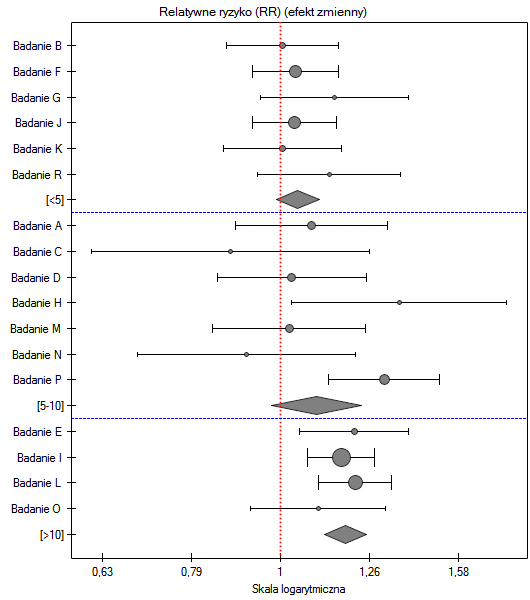
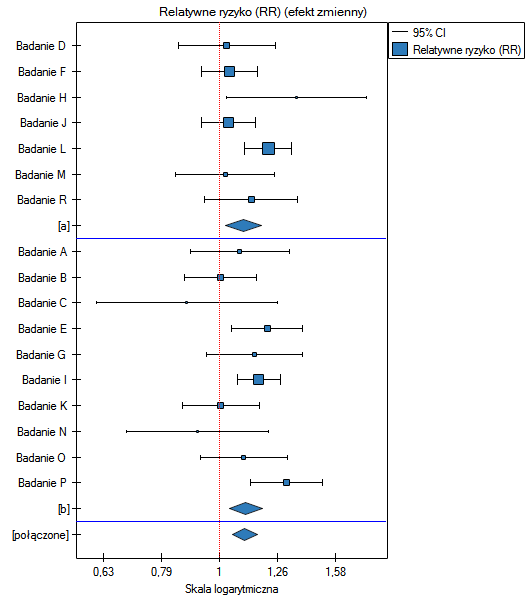
Ze względu na to, że prace włączone do meta-analizy pochodziły z różnych ośrodków i obejmowały nieco inne populacje, podsumowania dokonano wybierając efekt zmienny (oddzielne T2). Jako efekt końcowy wybrano relatywne ryzyko oraz przedstawiono wyniki na wykresie leśnym.

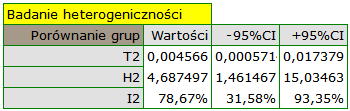
Grupy różnią się istotnie statystycznie (p=0.0092), co obserwujemy nie tylko na bazie testu heterogeniczności, ale również współczynnika H2 (współczynnik wraz z przedziałem ufności znajduje się powyżej wartości jeden) oraz I2 (78%, to wysoka heterogeniczność). Dlatego zebrane prace nie zostaną podsumowane wspólnym efektem a jedynie poprzez oddzielne podsumowanie każdej grupy.
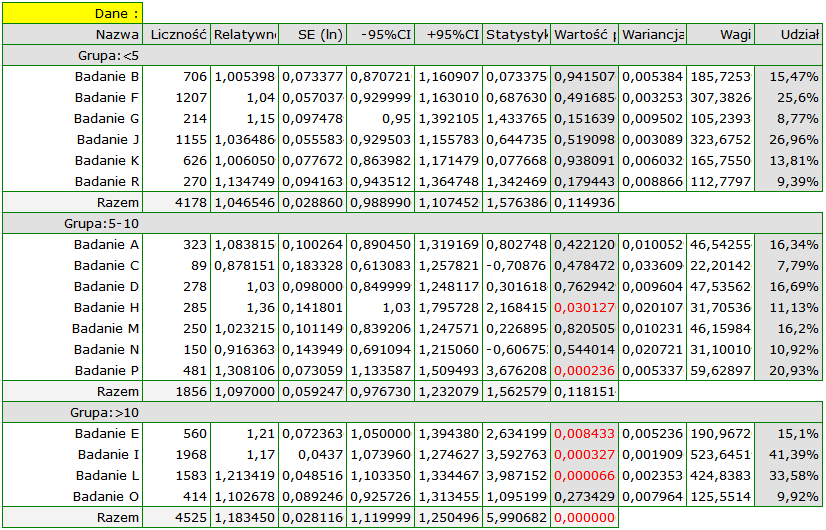
Wykres leśny również przedstawia podsumowanie każdej grupy i nie zawiera wspólnego podsumowania grup.
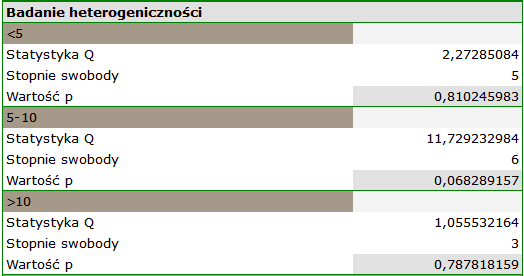
Dodatkowo sprawdzona została homogeniczność w każdej z grup, by upewnić się co do możliwości ich oddzielnego podsumowania.
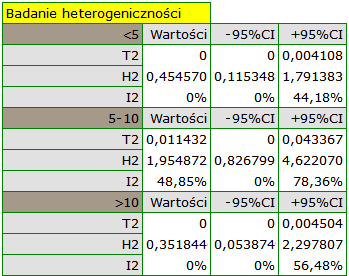
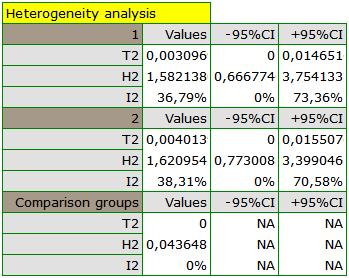
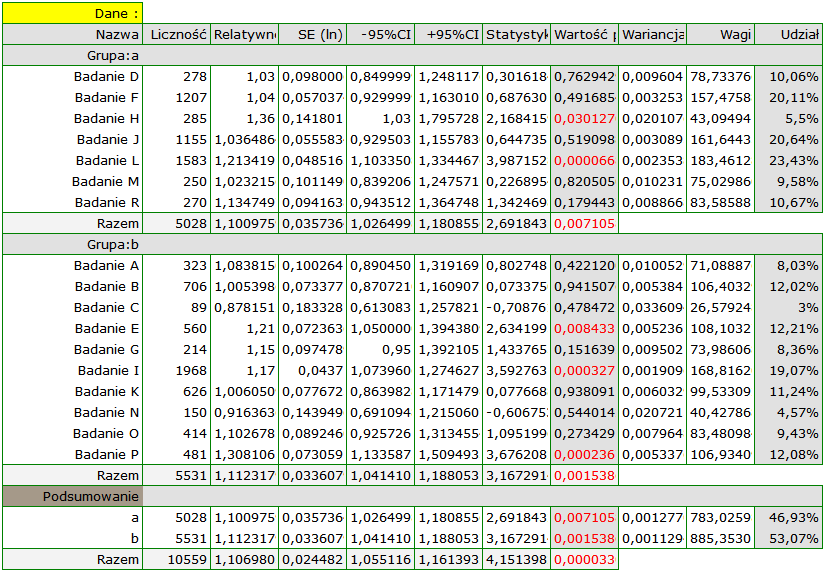
Wyniki porównania dotyczącego różnych warunków prowadzenia badań wskazują natomiast na brak istotnego wpływu tych warunków na efekt podsumowujący. W tym przypadku możliwy jest do wyliczenia wspólny efekt końcowy w korekcji o różne warunki przeprowadzania badań, czyli wspólne podsumowanie obu grup.

2018/03/04 11:58
· admin
statpqpl/metapl/porownanie.txt · ostatnio zmienione: 2018/03/04 13:01 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


