Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:statpqpl:aopisowapl:statopispl:miarpl
Location measures
Measures of central tendency
Measures of central tendency are so-called average measures that characterize the average or typical level of a trait's values.
Arithmetic mean is expressed by the formula:
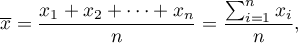
where  is the consecutive values of the variable and
is the consecutive values of the variable and  is the sample size.
is the sample size.
The arithmetic mean is used for interval scale. For a sample it is taken to be denoted by 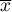 and for a population by
and for a population by 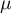 .
.
Trimmed mean - is determined as the arithmetic mean calculated after removing from the sample a given percentage of the smallest and largest measurements, e.g. if we cut off 5 per cent of the measurements, it means that we cut off 2.5 per cent of the largest and 2.5 per cent of the smallest values. At the same time, if the number of measurements to be removed obtained from the conversion is not an integer, it is rounded down to the nearest whole number.
Winsor mean - is determined as the arithmetic mean calculated after replacing the appropriate percentage of extreme measurements with the smallest and largest value that remains of the reduced set of values. If we choose to calculate the Winsor average by pruning, say, 5% of the measurements, then those discarded 5% will be replaced by the smallest and largest value determined from the remaining 95% of the measurements. As with the pruned average, when converting the percentage of values to be replaced to the number of measurements to be replaced does not result in an integer, then we round down to the nearest integer.
Geometric mean is expressed by the formula:
![LaTeX \begin{displaymath}
\overline{x}_G=\sqrt[n]{x_1x_2...x_n}=\sqrt[n]{\prod_{i=1}^n x_i}.
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img011017a5d163d0e6305611f865ade072.png) This mean is used for the interval scale, when the variable has a log-normal distribution (the logarithm of the variable has a normal distribution).
This mean is used for the interval scale, when the variable has a log-normal distribution (the logarithm of the variable has a normal distribution).
Harmonic mean is expressed by the formula:
 This mean is used for the interval scale.
This mean is used for the interval scale.
In an ordered data set, the median is the value that divides the data set into two equal parts. Half of all observations are below and half are above the median.
![LaTeX \begin{pspicture}(0,0)(3,4.6)
\pscoil[coilaspect=0, coilarm=.1cm, linewidth=0.5pt, coilwidth=.5cm, coilheight=1]{-}(0,4)
\rput(0,4.2){min}
\rput(0,-.2){max}
\psline(-0.35,2)(.35,2)
\rput(1.2,2){median}
\rput(-0.6,2.8){50$\%$}
\rput(-0.6,1.2){50$\%$}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img9b976478cd579bfe4153c57aa2d6d11a.png)
The median can be used in interval and ordinal scale.
Mode  is the value that occurs most frequently among the measurements obtained. Fashion can be used at any measurement scale.
is the value that occurs most frequently among the measurements obtained. Fashion can be used at any measurement scale.
2022/02/09 12:56
Other measures of location
![LaTeX \begin{pspicture}(0,-.2)(4,4.4)
\pscoil[coilaspect=0, coilarm=.1cm, linewidth=0.5pt, coilwidth=.5cm, coilheight=1]{-}(0,4)
\rput(0,4.2){max}
\rput(0,-.2){min}
\psline(-0.35,3)(.35,3)
\psline(-0.35,2)(.35,2)
\psline(-0.35,1)(.35,1)
\rput(2.9,3){$C_{75}$ = upper quartile = $Q_3$}
\rput(2.4,2){$C_{50}$ = median = $Q_2$}
\rput(2.9,1){$C_{25}$ = lower quartile = $Q_1$}
\rput(1,3.5){25$\%$}
\rput(1,2.5){25$\%$}
\rput(1,1.5){25$\%$}
\rput(1,.5){25$\%$}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img69d36b9c4fb1b5c0f0c2dccadaee5151.png)
Quartiles (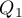 ,
, 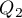 ,
, 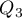 ) divide the ordered series into 4 equal parts, deciles (
) divide the ordered series into 4 equal parts, deciles (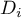 ,
, 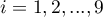 ) into 10 equal parts and centiles (percentiles:
) into 10 equal parts and centiles (percentiles: 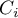 ,
, 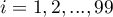 ) into 100 equal parts. The second quartile, fifth decile, and fiftieth centile are equal to the median. These measures can be used in the interval and ordinal scale.
) into 100 equal parts. The second quartile, fifth decile, and fiftieth centile are equal to the median. These measures can be used in the interval and ordinal scale.
2022/02/09 12:56
en/statpqpl/aopisowapl/statopispl/miarpl.txt · ostatnio zmienione: 2022/03/14 11:25 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

