Spis treści

Working with datasheets

Working with datasheets

The most important part of any project is the datasheet. Every open project must have at least one.

Dodawanie, usuwanie i eksport

Pierwszy pusty arkusz danych jest otwierany automatycznie wraz z nowym projektem. Kolejne arkusze danych mogą być dołączane do projektu przez:

menu Plik→Nowy arkusz (Ctrl+D)
przycisk Nowy arkusz w Zarządcy Projektu.

Usunięcie arkusza danych możliwe jest przez:

menu kontekstowe Usuń arkusz (Shift+Del) na nazwie arkusza danych w Drzewie nawigacji,
przycisk →Usuń w Zarządcy Projektu, gdy zaznaczony jest arkusz/arkusze.

Należy jednak pamiętać, że jeśli do arkusza danych dołączone są raporty lub mapa, to usuwając arkusz danych usuwa się jednocześnie wszystkie przypisane do niego raporty/mapę. Arkusze możemy opisać w Zarządcy Projektu dodając nazwę, wpisując tytuł lub dłuższą notatkę. Arkusze danych utworzone w PQStat można eksportować do formatu csv (txt), dbf i xls. Eksportu danych dokonuje się w Zarządcy Projektu przez przycisk →Eksportuj…, gdy zaznaczony jest arkusz/arkusze.

2014/08/22 20:00

Umieszczanie danych

Arkusze danych po utworzeniu są puste. Użytkownik sam wprowadza dane, kopiuje wcześniej przygotowane dane z innego arkusza danych lub importuje. Ilość danych, jaką mieści arkusz jest ograniczona do 4 milionów wierszy i 1000 kolumn. W każdej komórce może się znajdować maksymalnie 40 znaków.

Import danych

Dane można w prosty sposób importować z plików zapisanych w formacie:

*.xls/*xlsx,
*.txt/*.csv z wewnętrznym kodowaniem znaków UTF8, Windows-1250,
*.shp (SHP/SHX/DBF ESRI Shapefile),
*.dbf (dBase III, dBase IV, dBase VII),
*.sav (Spss),
*.dbf (FoxPro).

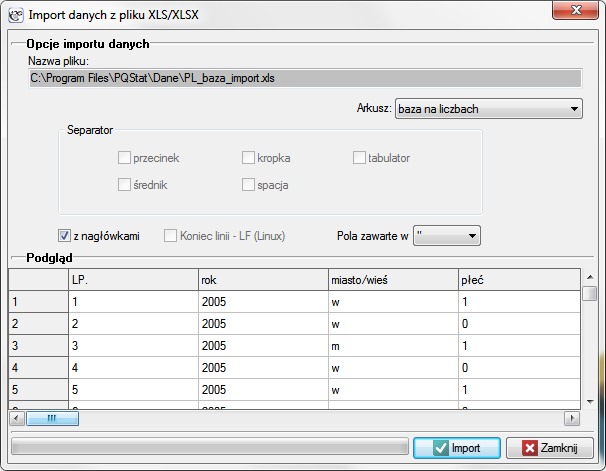
Importu dokonujemy wybierając z menu Plik→Importuj dane …

W oknie importu mamy możliwość podglądu importowanych danych i wcześniejszego sprawdzenia wyniku importu w zależności od ustalonych opcji dotyczących sposobu interpretacji danych. Aby uniknąć błędnej interpretacji znaków narodowych należy zwrócić szczególną uwagę na poprawność wyświetlania tych znaków w oknie podglądu. W przypadku dużych plików okno podglądu zawiera tylko początkową część danych z pliku.

Uwaga! W programach Microsoft Office Excel 2000-2007 domyślne kodowanie znaków to Windows-1250. Import danych z dokumentów Microsoft Excel dotyczy tylko wartości komórek, nie ma możliwości importu formatowania oraz formuł.

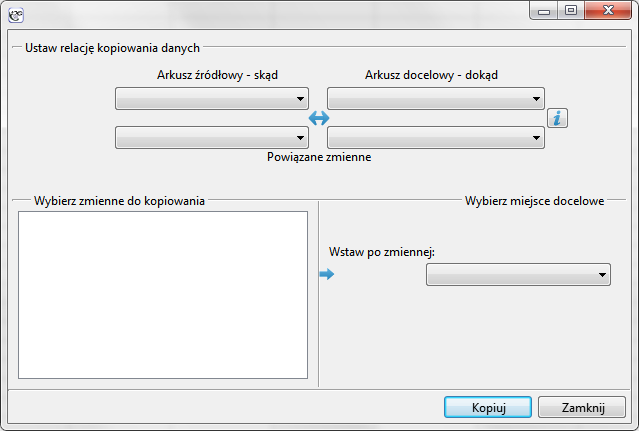
Kopiowanie danych poprzez relacje Do wybranego arkusza danych mogą zostać przekopiowane dane z innego arkusza na podstawie relacji. Ten rodzaj kopiowania danych wykonujemy wybierając z menu Dane→Kopiowanie z relacją…

By zbudować relację, należy wskazać arkusz danych, z którego dokonujemy kopiowania i arkusz danych, w którym umieścimy skopiowane dane. Oba te arkusze muszą posiadać ten sam klucz tzn. zmienną, której wartości identyfikują każdy wiersz w arkuszu. Wymagane jest aby klucz dla arkusza źródłowego był unikalny. Powiązanie odbywa się według relacji jeden-do-wielu, czyli jeden wiersz z arkusza źródłowego może być powiązany z wieloma wierszami z arkusza docelowego. Klucze obu arkuszy należy wybrać jako Powiązane zmienne. Dla tak ustawionej relacji wskazujemy zmienne do kopiowania i kolumnę po której mają zostać umieszczone przekopiowane zmienne.

2014/08/22 20:00

Okno arkusza

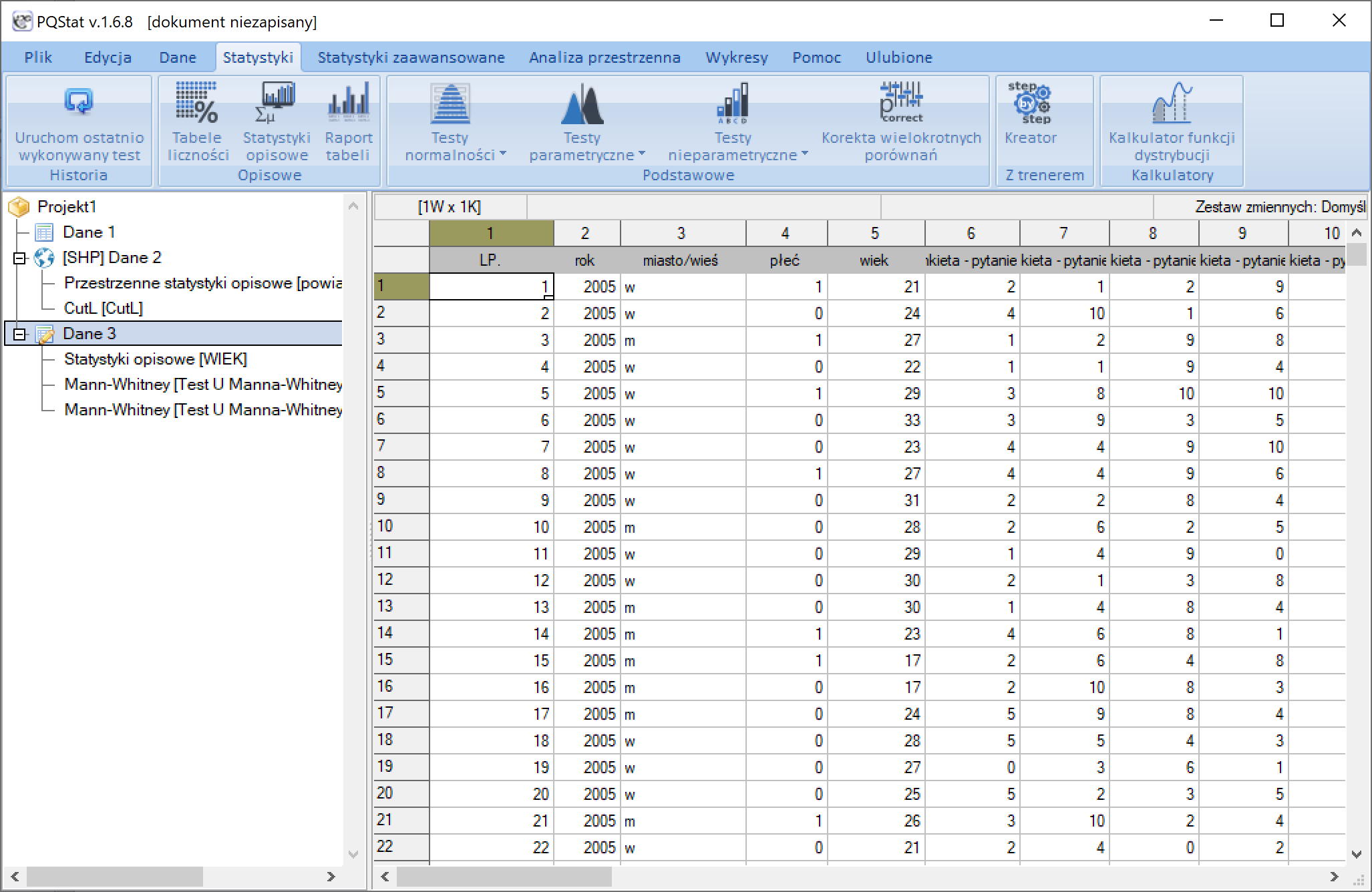
Wiersze i kolumny arkusza danych oznaczone są poprzez kolejne liczby naturalne. Każdej kolumnie w miejscu oznaczonym szarym kolorem można nadać własny nagłówek. Na górze arkusza znajduje się Pasek komunikatów. Jest to miejsce, w którym wyświetlane są bieżące informacje dla użytkownika. Lewa część paska informuje o wielkości zaznaczonego obszaru [liczba wierszy, liczba kolumn], środkowa wyświetla wartość znajdującą się w zaznaczonej komórce, a prawa część przeznaczona jest na informacje dla użytkownika dotyczące min. wykonywanej analizy statystycznej.

2014/08/22 20:00

Właściwości zmiennej

Dla każdej kolumny arkusza możemy ustawić jej właściwości takie jak kody, etykiety i format. Ustawienie właściwości zmiennej jest możliwe po

wybraniu Właściwości zmiennej→Kody/Etykiety/Format z menu kontekstowego na numerze znajdującym się powyżej nagłówka kolumny,
po podwójnym kliknięciu na numerze znajdującym się powyżej nagłówka kolumny - o ile tak zaznaczono w ustawieniach programu (odpowiednia akcja podwójnego kliknięcia).

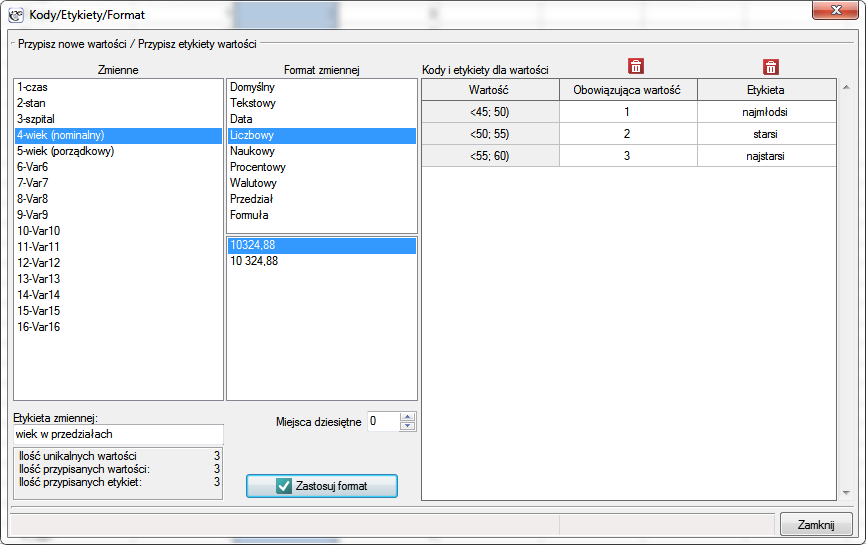Kody i etykiety dla wartości – są możliwe do przypisania dla każdej wartości, która występuje w danej kolumnie.

Obowiązująca wartość - Wypełniając kody ustawiamy wartości jakie mają obowiązywać w danej kolumnie. W rezultacie wartości pobierane do obliczeń zostaną zmienione (w tle) na odpowiednio przypisane kody (obowiązujące wartości).
Etykieta - Wartości jakie wpisane zostaną w polu Etykieta wykorzystywane są w raportach i na wykresach dla ustalonego przez użytkownika opisu wyników.

Etykieta zmiennej - jest przypisywana do nagłówka danej kolumny. Zwykle jest to krótki opis zawartości zmiennej. Ustawiona etykieta zmiennej wykorzystywana jest zamiast nagłówka kolumny (nazwy zmiennej) w raportach i na wykresach dla czytelniejszego opisu wyników. Wykorzystanie etykiety zmiennej jest opcjonalne i zależy od ustawień programu.

Format komórek

Każda komórka arkusza (również nagłówek kolumny) może zawierać najwyżej 40 znaków. Dozwolone są również teksty zawierające znaki narodowe. Wprowadzone wartości mogą być sformatowane jako:

domyślne - format domyślny jest formatem, w którym program automatycznie rozpoznaje zawartość komórki w zakresie - dane liczbowe, dane tekstowe;
tekstowe - w formacie tekstowym dane interpretowane są jako tekst (wyrównanie do lewej krawędzi komórki);
data - w formacie daty dane liczbowe interpretowane są jako kolejne wartości daty, i tak wartość 1 oznacza 1899.12.31, wartość 2 oznacza 1900.01.01 itd. W zależności od wybranego formatu daty można również wprowadzać dane tekstowo w wybranym formacie, są to:

2010.12.31

31.12.2010

12.31.2010

2010/12/31

31/12/2010

12/31/2010

2010-12-31

31-12-2010

12-31-2010

Poniedziałek…

Styczeń…

W przypadku formatu Poniedziałek… wartość 1 oznacza poniedziałek, …, 7 - niedziela, w przypadku formatu Styczeń…, wartość 1 oznacza styczeń, …, 12 - grudzień.

czas - w formacie czasu dane liczbowe interpretowanie są jako kolejne wartości czasu, część ułamkowa liczby oznacza ilość milisekund od północy podzielonych przez całkowitą ilość milisekund dnia (86400000), i tak wartość 0,000694444 oznacza 00:01:00, wartość 0,041666667 oznacza 01:00:00, wartość 0,999988426 oznacza 23:59:59. W zależności od wybranego formatu czasu można również wprowadzać dane tekstowo w wybranym formacie, są to:

18:31:58

18:31

12/31/2010 18:31

12/31/2010 18:31:58

liczbowe - liczby rzeczywiste w tym formacie występują w postaci rozwinięcia dziesiętnego, przy czym znak oddzielający część całkowitą i ułamkową to przecinek lub kropka (w zależności od ustawień wybranych w oknie ''Ustawienia'' w polu Separator dziesiętny), możliwe jest ustawienie liczb miejsc dziesiętnych oraz separatora części tysięcznych;
naukowe - czyli przy użyciu 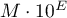$M \cdot 10^E$ , gdzie podstawa, to mantysa 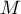$M$ , a wykładnik 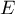$E$ jest liczbą całkowitą; tak jak w formacie liczbowym możliwe jest ustawienie liczby miejsc dziesiętnych;
procentowe - zmieniające liczbę na procent poprzez pomnożenie przez 100 i wyświetlenie z symbolem %; tak jak w formacie liczbowym możliwe jest ustawienie liczby miejsc dziesiętnych;
walutowe - wykorzystywane są dla wartości pieniężnych - pozwala to na dodanie symbolu waluty; tak jak w formacie liczbowym możliwe jest ustawienie liczby miejsc dziesiętnych;
przedział - zapisany za pomocą górnej i dolnej granicy; tak jak w formacie liczbowym możliwe jest ustawienie liczby miejsc dziesiętnych;
formuła - wartości wyliczone zgodnie z przypisaną do kolumny formułą; wartość jest automatycznie przeliczana gdy zmieniona zostanie którakolwiek z danych wejściowych.

Po otwarciu nowego arkusza dla każdej komórki ustawiony jest standardowo format domyślny.

Cały wiersz nagłówkowy ma na stałe ustawiony format tekstowy. Dla pozostałej części arkusza istnieje możliwość ustawienia przez użytkownika zdefiniowanych formatów. Formatowaniu nie podlega pojedyncza komórka, ale cała kolumna (za wyjątkiem jej nagłówka).

W arkuszu można określić szerokość kolumny przy użyciu myszy. W tym celu należy przy pomocy wskaźnika myszy przeciągnąć linię dzielącą kolumny, zwężając lub rozszerzając kolumnę znajdującą się po lewej stronie wybranej linii.

Dodatkowo w każdej komórce arkusza można ustalić inny kolor tła (po uprzednim zaznaczeniu zmienianego obszaru). Służy do tego:

- menu Edycja→Kolor wypełnienia…

- polecenie Kolor komórki w menu kontekstowym komórki.

2014/08/22 20:00

Edycja danych

Zaznaczanie spójnego obszaru arkusza może się odbywać przy pomocy myszy lub klawiatury (Klawisze strzałek + Shift). Podczas zaznaczenia na bieżąco na pasku komunikatów jest wyświetlany jego rozmiar (liczba wierszy i kolumn). Cały arkusz można zaznaczyć w prosty sposób myszą klikając w lewy górny róg arkusza lub wybierając z menu Edycja→Zaznacz wszystko (Ctrl+A). Całe wiersze lub całe kolumny zaznaczamy wybierając ich nagłówki.

Kopiowanie lub przenoszenie komórek dokonuje się poprzez polecenia kopiuj, wytnij i wklej.

Polecenia kopiuj, wytnij i wklej są dostępne w kilku miejscach:

- w menu Edycja,

- w menu kontekstowym komórek,

- na pasku narzędziowym ,

- w menu kontekstowym wierszy i kolumn,

- przez klawisze skrótów: kopiuj (Ctrl+C), wytnij (Ctrl+X), i wklej (Ctrl+V).

Usuwanie danych z komórek można wykonać poprzez menu Edycja→Usuń (Del)

Cofanie ostatnio wykonywanej operacji można wykonać poprzez menu Edycja→Cofnij (Ctrl+Z). Standardowo Program pamięta 10 ostatnich operacji dotyczących 5000 komórek w każdej z nich. Ustawienia te można zmienić w oknie ''Ustawienia.'' Należy zaznaczyć jednak, iż zwiększanie tych wartości niesie za sobą większe użycie pamięci komputera przez program.

Wstawianie i usuwanie wierszy i kolumn

Można wstawić puste wiersze lub kolumny powyżej lub po lewej stronie istniejącego wiersza lub kolumny. Spowoduje to przesunięcie komórek w dół lub w prawo. Aby wstawić wiersz/wiersze należy zaznaczyć ten wiersz/wiersze powyżej którego chcemy wstawić nowy wiersz/wiersze, a następnie wybrać z menu kontekstowego na numerze zaznaczonego wiersza Wstaw wiersz. W analogiczny sposób dokonuje się wstawianie kolumn.

Wiersze i kolumny można również usuwać poprzez ich zaznaczenie i wybranie w menu kontekstowym na numerze wiersza lub kolumny Usuń wiersz/Usuń kolumnę.

Znajdowanie/zamiana wartości komórki

By wyszukać lub zastąpić całą zawartość komórki inną wartością używa się okna Znajdź/Zamień, które wywołujemy poprzez menu Edycja→Znajdź/Zamień (Ctrl+F) .

Górna część okna Znajdź/Zamień służy wyszukiwaniu a dolna zamianie wartości komórki.

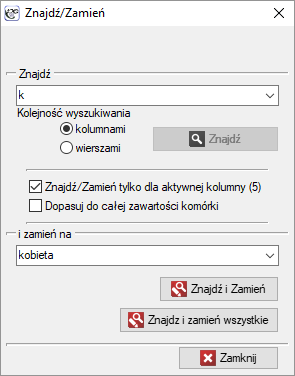
Aby wyszukać dane, w górnej części okna należy wpisać szukany ciąg znaków oraz zaznaczyć kolejność wyszukiwania i wybrać przycisk Znajdź.

Aby znaleźć i zastąpić całą zawartość komórki inną wartością należy wypełnić górną i dolną część okna. Górną część okna wypełniamy tak jak w przypadku wyszukiwania danych. W dolnej części okna wpisujemy dane, które mają zastąpić wyszukane i wybieramy przycisk Znajdź i Zamień lub Znajdź i zamień wszystkie, gdy chcemy zastąpić wszystkie wystąpienia wyszukanych danych. Wyszukiwanie jak i zamiana odbywa się w trybie bezpośredniego podglądu wykonywanych operacji na arkuszu.

2014/08/22 20:00

Sortowanie danych

Opcje sortowania dostępne są po wybraniu z menu Dane→Sortuj… lub opcji Sortuj… z menu kontekstowego na numerze znajdującym się powyżej nagłówka kolumny. Zwykle sortujemy cały arkusz danych (takie jest ustawienie domyśle dotyczące sortowania), jeśli jednak sortowanie rozpoczniemy od zaznaczenia fragmentu danych, wówczas w oknie sortowania będziemy mieli możliwość ograniczenia obszaru sortowania tylko do zaznaczenia.

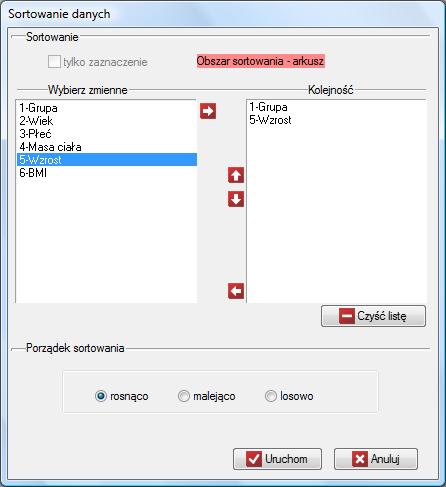
W oknie sortowania za pomocą strzałek przenosimy z pola Wybierz zmienne do pola Kolejność te zmienne, według których chcemy sortować dane, a następnie wybieramy Porządek sortowania i potwierdzamy wybór przyciskiem Uruchom.

Sortować możemy według co najwyżej 3 kolumn (zmiennych). Jeśli sortujemy dane według więcej niż jednej zmiennej to sortowanie odbywa się w takiej kolejności, w jakiej znajdują się zmienne umieszczone w polu Kolejność.

2014/08/22 20:00

Zamiana danych surowych na tabelę kontyngencji

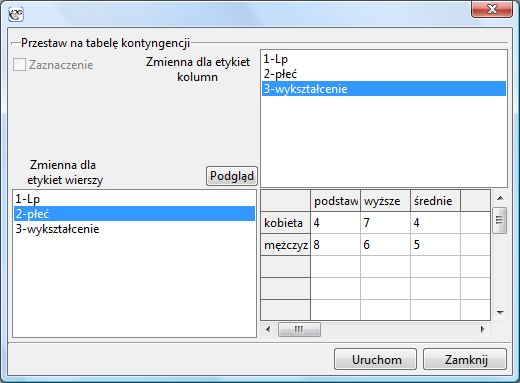
Operacja zamiany danych surowych na tabelę kontyngencji dostępna jest po wybraniu z menu Dane→Przestaw na tabelę…

Zwykle dla tej operacji dostępny jest cały arkusz danych (takie jest ustawienie domyśle), jeśli jednak przekształcanie rozpoczniemy od zaznaczenia fragmentu danych, wówczas w oknie przekształcania danych będziemy mieli możliwość ograniczenia dostępnego obszaru tylko do zaznaczenia.

Tabelę kontyngencji projektujemy wybierając zmienne tworzące etykiety wierszy i kolumn. Jeśli podgląd tabeli zgodny jest z oczekiwanym wynikiem, wówczas dokonany wybór potwierdzamy przyciskiem Uruchom. Zwrócony wynik umieszczony zostanie w nowym arkuszu.

2014/08/22 20:00

Zamiana tabeli kontyngencji na dane surowe

Operacja zamiany tabeli kontyngencji na dane surowe dostępna jest po wybraniu z menu Dane→Przestaw na dane surowe… W oknie przekształcania danych wpisujemy odpowiednie liczności oraz nagłówki wierszy i kolumn i dokonany wybór potwierdzamy przyciskiem Uruchom. Zwrócony wynik umieszczony zostanie w nowym arkuszu.

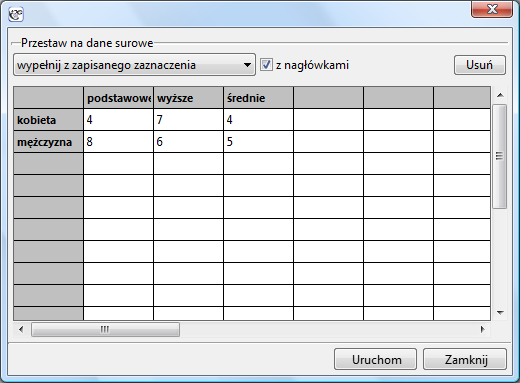
Jeśli przekształcamy tabelę, która znajduje się w arkuszu danych, wówczas przed przystąpieniem do zamiany tej tabeli na dane surowe zaznaczamy ją (z nagłówkami lub bez). Wówczas w oknie przekształcania danych tabela ta zostanie umieszczona automatycznie. Możliwe jest także wykorzystanie innych tabel oznaczonych jako zapisane zaznaczenie.

2014/08/22 20:00

Formuły

Definiowanie formuły jest sposobem na przeliczenie danych, w wyniku którego uzyskujemy nowe wartości dla zmiennych.

Okno definiowania formuł wywołujemy poprzez Dane→Formuły…

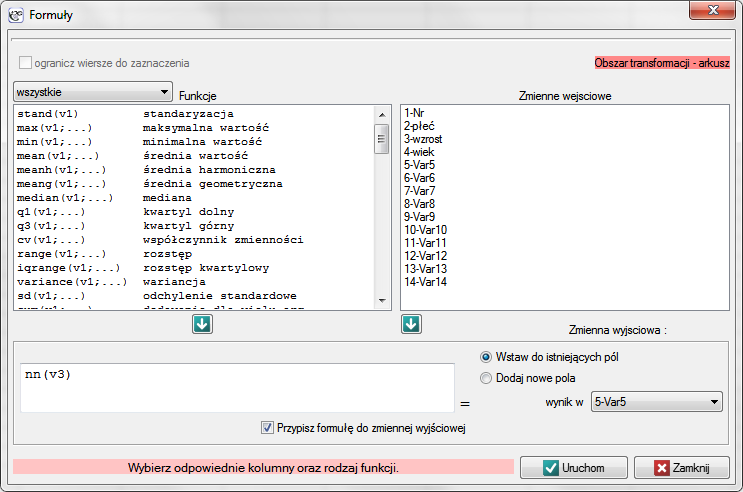
Formuły przypisane do danej zmiennej arkusza jako format tej zmiennej są zapamiętywane wraz z arkuszem danych. Ich wynik zostaje automatycznie przeliczony, gdy zmieniona zostanie którakolwiek z danych wejściowych. Przypisania formuły można dokonać w oknie Formuły… lub poprzez ustawienie Formatu kolumny (Ctrl+F10).

Budowanie formuł

Formuły wprowadzamy w polu edycji

Zmienne, do których odwołują się formuły, wprowadzamy podając ich numery np. v1+v2
Wartości tekstowe wpisujemy używając apostrofu np. 'dom'
Funkcje wprowadzamy poprzez dwukrotne kliknięcie na nazwie wybranej funkcji - wówczas nazwa ta pojawi się w polu edycji formuły, lub samodzielnie wpisujemy nazwę w polu edycji, przy czym wielkość liter w nazwie funkcji nie ma znaczenia. Argumenty funkcji podajemy w nawiasie stosując składnię podaną w opisie funkcji.

Wyniki formuł

Wyniki formuł zostaną wyświetlone w wybranej kolumnie.

Jeżeli wśród argumentów funkcji wystąpią wartości, których funkcja nie potrafi zinterpretować, to program wyświetli komunikat pytający czy pominąć zmienne niezinterpretowane. Udzielenie odpowiedzi twierdzącej spowoduje przeliczenie formuły z pominięciem danych niezinterpretowanych. W przypadku udzielenia odpowiedzi przeczącej formuła zwróci błąd (NA). Przykładowo dla wartości w kolumnach v1, v2 i v3 odpowiednio: 1, 2, 'ada', funkcja sumowania sum(v1;v2;v3) zwróci wynik 3 - gdy pominiemy niezinterpretowaną wartość 'ada', lub zwróci NA - gdy nie pominiemy tej wartości w obliczeniach.

Wartość pusta (brak danych) zostanie zwrócona tylko wtedy, gdy wszystkie argumenty wykorzystywane w formule są puste.

Ilość wierszy biorących udział w formule możemy ograniczyć zaznaczając w arkuszu danych odpowiedni zakres wierszy i wybierając w oknie formuły opcję ogranicz wiersze do zaznaczenia.

Operatory

$+$ dodawanie,

$-$ odejmowanie,

$*$ mnożenie,

$/$ dzielenie,

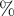$\%$ dzielenie modulo (w wyniku reszta z dzielenia),

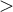$>$ większy,

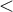$<$ mniejszy,

$=$ równy.

Funkcje matematyczne

Funkcje matematyczne wymagają argumentów liczbowych.

ln(v1) - zwraca logarytm naturalny podanej liczby,

log10(v1) - zwraca logarytm przy podstawie 10 dla podanej liczby,

logn(v1) - zwraca logarytm przy podstawie $n$ dla podanej liczby,

sqr(v1) - zwraca kwadrat podanej liczby,

sqrt(v1) - zwraca pierwiastek kwadratowy podanej liczby,

fact(v1) - zwraca silnię podanej liczby,

degrad(v1) - zwraca miarę kąta w radianach (argumentem funkcji są stopnie),

raddeg(v1) - zwraca miarę kąta w stopniach (argumentem funkcji są radiany),

sin(v1) - zwraca sinus podanego kąta, (argumentem funkcji są radiany),

cos(v1) - zwraca cosinus podanego kąta, (argumentem funkcji są radiany),

tan(v1) - zwraca tangens podanego kąta, (argumentem funkcji są radiany),

ctng(v1) - zwraca cotangens podanego kąta, (argumentem funkcji są radiany),

arcsin(v1) - zwraca arcus sinus podanego kąta, (argumentem funkcji są radiany),

arctan(v1) - zwraca arcus tangens podanego kąta, (argumentem funkcji są radiany),

exp(v1) - zwraca wartość liczby 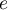$e$ podniesionej do potęgi określonej przez podaną wartość,

frac(v1) - zwraca część ułamkową podanej liczby,

int(v1) - zwraca część całkowitą podanej liczby,

abs(v1) - zwraca wartość bezwzględną podanej liczby,

odd(v1) - zwraca 1, gdy podana liczba jest parzysta, 0 w przeciwnym przypadku,

sum(v1;…) - zwraca wynik dodawania podanych liczb,

multip(v1;…) - zwraca wynik mnożenia podanych liczb,

power(v1;n) - zwraca wynik podniesienia liczby do potęgi $n$ ,

norme(v1;…) - zwraca normę euklidesową wektora,

round(v1;n) - zwraca liczbę zaokrągloną do $n$ miejsc po przecinku.

Funkcje statystyczne

Funkcje statystyczne wymagają argumentów liczbowych.

stand(v1) - zwraca wystandaryzowaną wartość podanej zmiennej,

max(v1,…) - zwraca wartość największą,

min(v1,…) - zwraca wartość najmniejszą,

mean(v1,…) - zwraca wartość średniej arytmetycznej,

meanh(v1,…) - zwraca wartość średniej harmonicznej,

meang(v1,…) - zwraca wartość średniej geometrycznej,

median(v1,…) - zwraca wartość mediany,

q1(v1,…) - zwraca wartość kwartyla dolnego,

q3(v1,…) - zwraca wartość kwartyla górnego,

cv(v1,…) - zwraca wartość współczynnika zmienności,

range(v1,…) - zwraca wartość rozstępu,

iqrange(v1,…) - zwraca wartość rozstępu kwartylowego,

variance(v1,…) - zwraca wartość wariancji,

sd(v1,…) - zwraca wartość odchylenia standardowego.

Funkcje tekstowe

Funkcje tekstowe działają na dowolnym ciągu znaków.

upperc(v1) - konwertuje znaki z łańcucha na wielkie,

lowerc(v1) - konwertuje znaki z łańcucha na małe,

clean(v1) - usuwa znaki, które nie mogą być drukowane,

trim(v1) - usuwa przednie i końcowe spacje,

length(v1) - zwraca długość łańcucha znaków,

search('abc';v1) - zwraca pozycję początku szukanego tekstu,

concat(v1;…) - łączy teksty,

compare(v1;…) - porównuje teksty,

copy(v1;i;n) - zwraca część tekstu począwszy od i-tego znaku, gdzie n - to ilość zwracanych znaków,

count(v1;…) - zwraca ilość komórek, które nie są puste,

counte(v1;…) - zwraca ilość pustych komórek,

countn(v1;…) - zwraca ilość komórek, które zawierają liczby.

Funkcje daty i czasu

Funkcje daty i czasu powinny być wykonywane na danych sformatowanych jako data lub jako czas (patrz format). Jeśli tak nie jest, program stara się automatycznie rozpoznać format, a gdy nie jest to możliwe zwraca wartość NA.

year(v1;) - zwraca rok odpowiadający dacie,

month(v1;) - zwraca miesiąc odpowiadający dacie,

day(v1;) - zwraca dzień odpowiadający dacie,

hour(v1;) - zwraca godzinę odopowiadającą podanemu czasowi,

minute(v1;) - zwraca minutę odopowiadającą podanemu czasowi,

second(v1;) - zwraca sekundę odopowiadającą podanemu czasowi,

yeardiff(v1;v2) - zwraca liczbę lat różniącą dwie daty,

monthdiff(v1;v2) - zwraca liczbę miesięcy różniącą dwie daty,

weekdiff(v1;v2) - zwraca liczbę tygodni różniącą dwie daty,

daydiff(v1;v2) - zwraca liczbę dni różniącą dwie daty,

hourdiff(v1;v2) - zwraca liczbę godzin różniącą dwa czasy,

minutediff(v1;v2) - zwraca liczbę minut różniącą dwa czasy,

seconddiff(v1;v2) - zwraca liczbę sekund różniącą dwa czasy,

compdate(v1;v2) - porównuje daty i zwraca liczbę 1 gdy v1>v2; 0 gdy v1=v2, -1 gdy v1<v2.

Funkcje logiczne

if(pytanie;'tak - odpowiedź';'nie - odpowiedź') - pytanie formułuje się w formie twierdzenia, które może być prawdziwe lub fałszywe; funkcja zwraca jedną wartość jeśli twierdzenie jest prawdziwe a drugą jeśli jest fałszywe,

and - operator koniunkcji - zwraca prawdę (1) gdy wszystkie warunki, które łączy są prawdziwe, fałsz (0) w przeciwnym wypadku,

or - operator alternatywy zwraca prawdę (1) gdy przynajmniej jeden z łączonych przez nią warunków jest prawdziwy, fałsz (0) w przeciwnym wypadku,

xor - operator alternatywy rozłącznej - zwraca prawdę (1) gdy jeden z łączonych przez nią warunków jest prawdziwy, fałsz (0) w przeciwnym wypadku,

not - operator negacji używany w wyrażeniu warunkowym if,

empty(v1) - zwraca prawdę (1) gdy występują puste komórki, fałsz (0) w przeciwnym przypadku,

text(v1) - zwraca prawdę (1) gdy występuje tekst, fałsz (0) w przeciwnym przypadku,

number(v1) - zwraca prawdę (1) gdy występuje liczba, fałsz (0) w przeciwnym przypadku.

2014/08/22 20:00

Generowanie danych

Istnieją dwie metody generowania danych:

Pierwsza metoda korzysta z prostego przeciągnięcia zawartości z zaznaczonych komórek na komórki sąsiednie przy pomocy wskaźnika myszy. Metoda ta pozwala na generowanie takich samych wartości (tekstowych lub liczbowych) w sąsiednich kolumnach bądź wierszach. Generowanie rozpoczynamy od wyboru komórki z odpowiednim wpisem, a następnie chwytamy wskaźnikiem myszy obrazującym znak $+$ prawy dolny narożnik tej komórki i przytrzymując przeciągamy przez komórki, które chcemy wypełnić. Przeciąganie pojedynczej komórki możemy wykonać w dowolnym kierunku ( w górę w dół w lewo i w prawo). Możliwe jest również przeciąganie różnych wartości umieszczonych w jednej kolumnie (w lewo bądź w prawo) lub w jednym wierszu (w górę bądź w dół).
Druga metoda pozwala na generowanie danych liczbowych w kolumnach jako serii danych, wartości losowych oraz wartości losowych z odpowiedniego rozkładu danych.

By wygenerować dane liczbowe należy zaznaczyć komórkę, od której chcemy zacząć wypełnianie arkusza i wywołać okno generowania danych liczbowych poprzez menu Dane→Generuj…

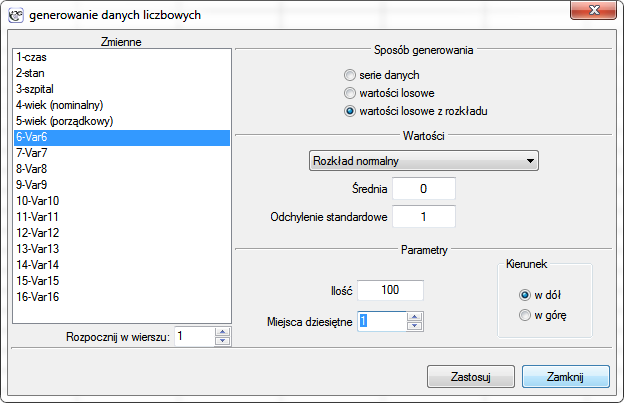
Zaczynamy od wyboru zmiennej, w której będą umieszczone wygenerowane dane.

W części środkowej okna w zależności od ustawień wybranego wyżej sposób generowania danych ustawiamy:

Dla generowania serii danych:

- Wartość początkowa - pierwsza wartość, która ma być wygenerowana,

- Krok - wartość, o jaką mają się różnić kolejne wygenerowane dane.

Dla generowania wartości losowych:

- Przedział (od) - początek przedziału, z którego będą losowane wartości,

- Przedział (do) - koniec przedziału, z którego będą losowane wartości.

Dla generowania wartości losowych z rozkładu wybieramy rodzaj rozkładu (Rozkład normalny, Rozkład Chi-kwadrat) i wpisujemy jego parametry.

Liczba wygenerowanych danych zależy od wartości, jaką użytkownik wpisze w polu ilość, a precyzja od ustawienia pola miejsca dziesiętne. Dane zostaną wpisane począwszy od aktywnej komórki w dół bądź w górę - w zależności od wybranej opcji. Ostatecznie potwierdzamy dokonany wybór przyciskiem Zastosuj.

2014/08/22 20:00

Braki danych

W badaniach bardzo często napotykamy na braki danych, jest to naturalne szczególnie dla danych ankietowych. Bywają sytuacje, w których braki danych wnoszą wartościową informację. Przykładowo: ilość braków danych w odpowiedzi na pytanie dotyczące sympatii do partii politycznych daje pogląd o ilości niezdecydowanych osób, które nie darzą sympatią (lub nie przyznają się że darzą sympatią) określonych ugrupowań politycznych. Niewielkie liczności braków danych nie stanowią problemu w analizach statystycznych. Duża ich ilość może jednak poddawać pod wątpliwość rzetelność przeprowadzonych badań. Warto już na początku pracy zadbać by było ich jak najmniej. Oczywiście najlepiej jest dotrzeć do informacji o rzeczywistej wartości, która powinna być wpisana w miejsce braku danych, jednak nie zawsze jest to możliwe.

Sposób w jaki szacowane są brakujące dane zależy przede wszystkim od charakteru danych. W programie zaproponowano kilka sposobów imputacji braków danych dla poszczególnych zmiennych.

Okno z ustawieniami opcji zastępowania braków danych wywołujemy poprzez menu Dane→Braki danych…

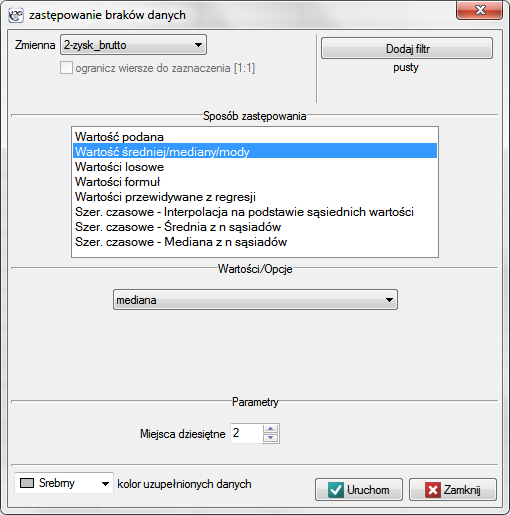
Wypełnianie jedną wartością
Wybranie jednej z poniższych opcji spowoduje zastąpienie w wybranej kolumnie wszystkich występujących tam braków tą samą wartością:
- podaną przez użytkownika,
- średnią arytmetyczną wyliczoną z danych,
- średnią geometryczną wyliczoną z danych,
- średnią harmoniczną wyliczoną z danych,
- medianą,
- modą (o ile nie jest wielokrotna).
Wypełnianie wieloma wartościami

Wybranie jednej z poniższych opcji spowoduje zastąpienie braków w wybranej kolumnie wieloma (najczęściej różnymi) wartościami. Wartości te mogą być przewidywane na podstawie kolumny, dla której następuje wypełnienie braków danych ale mogą być również przewidywane na podstawie wartości innych kolumn (zmiennych). Zastąpić brak danych możemy wartościami:

losowymi z danych;
losowymi z rozkładu normalnego - rozkład normalny definiowany jest na podstawie średniej i odchylenia standardowego z występujących danych;
losowymi z przedziału podanego przez użytkownika;
wyliczanymi z funkcji użytkownika - opcja ta pozwala na wykorzystanie danych z innych zmiennych by móc przewidzieć brakującą wartość w wybranej kolumnie;
wyliczanymi z modelu regresji - opcja ta pozwala na przewidywanie wartości braków danych na podstawie modelu regresji wielorakiej (zasada działania regresji wielorakiej opisana została w dziale ''Liniowa regresja wieloraka'');
interpolacja na podstawie sąsiednich wartości - dotyczy szeregów czasowych - użytkownik musi więc wskazać zmienną czas mówiącą o uporządkowaniu danych; interpolacja polega na wyznaczeniu wartości dla braków danych w ten sposób by graficznie znalazły się na linii prostej łączącej wartości dla danych sąsiadujących z brakami;
średnia z $n$ sąsiadów - dotyczy szeregów czasowych - użytkownik musi więc wskazać zmienną czas mówiącą o uporządkowaniu danych; interpolacja polega na wyznaczeniu średniej z wartości dla $n$ sąsiadów poprzedzających i $n$ sąsiadów następujących bezpośrednio po brakach danych;
mediana z $n$ sąsiadów - dotyczy szeregów czasowych - użytkownik musi więc wskazać zmienną czas mówiącą o uporządkowaniu danych; interpolacja polega na wyznaczeniu mediany z wartości dla $n$ sąsiadów poprzedzających i z $n$ sąsiadów następujących bezpośrednio po brakach danych;

Uwaga!

By można było odróżnić dane, które zostały imputowane od danych rzeczywistych, miejsca zastąpione oznaczane są wybranym kolorem.

Przykład (plik: brakiDanychWydawca.pqs)

Analiza pliku wydawca.pqs nie zawierającego braków danych została omówiona w dziale ''Liniowa regresja wieloraka''. Tym razem zajmiemy się arkuszem w którym w kolumnie zawierającej zysk brutto ze sprzedaży książek występują braki danych. W przypadku tych braków znane są wartości rzeczywiste (arkusz: „RZECZYWISTE DANE”), można zatem odnieść wartości wygenerowane w programie dla braków danych do wartości rzeczywistych by porównać wyniki uzyskane różnymi technikami. W przykładzie wykorzystamy 2 sposoby zastępowania braków danych: zastąpienie wartością mediany i wartością wyznaczoną na podstawie modelu regresji. Pozostałe możliwości pozostawiamy do samodzielnej pracy.

Zastąpienie braków danych wartością mediany wykonujemy na arkuszu pierwszym nazwanym „Wstaw medianę”. Ustawiamy w oknie Braków danych zmienną uzupełnianą jako zysk brutto i wybieramy sposób zastępowania jako wartość mediany. W rezultacie w miejsce braków danych wpisana zostanie wartość 46,85 tysięcy dolarów.

Podejrzewamy, że zyski są większe, gdy dotyczą książek znanych autorów (kodowanych jako 1) a mniejsze, gdy dotyczą tych nieznanych (kodowanych jako 0). Wyliczymy więc medianę zysku brutto oddzielnie dla książek autorów znanych i nieznanych. Imputację wykonujemy na arkuszu danych o nazwie „Wstaw dwie mediany”. Ustawiamy dwukrotnie filtr dla zmiennej definiującej popularność autora (zmienna 7) - raz podając wartość 1, a raz 0. Uzyskana mediana zysku brutto w grupie książek autorów popularnych to ok. 51 tysięcy dolarów, a wśród tych mniej znanych to ok. 34 tysiące dolarów.

Innym sposobem zastępowania braków jest np. skorzystanie z modelu regresji. Wybieramy arkusz danych „Wstaw z regresji” i ponownie wybieramy w oknie Braków danych zmienną dotyczącą zysku brutto jako zmienną, którą należy uzupełnić, jako sposób zastępowania wybieramy natomiast Wartości przewidywane z regresji. Zmiennych dzięki którym będziemy przewidywać wartość zysku brutto będzie tym razem więcej - będą to: koszty produkcji (zmienna 3), koszty reklamy (zmienna 4) i popularność autora (zmienna 7). Tym razem wyniki wydają się mniej odbiegać od rzeczywistych wartości, niestety brakuje wyniku dla pozycji o numerze 35. Dla tej książki nie mieliśmy bowiem informacji o koszcie produkcji na którym to między innymi chcieliśmy oprzeć przewidywanie.

2014/08/22 20:00

Transformacja

Okno transformacji danych wywołujemy poprzez Dane→Transformuj…

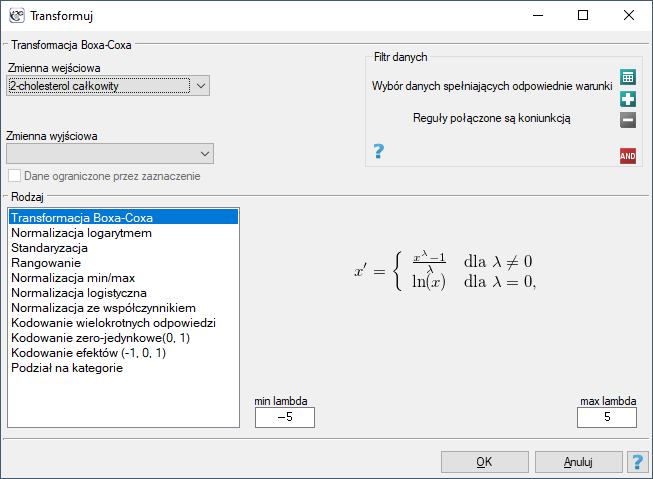
Transformacja danych to ich przekształcenie w taki sposób, by spełniały określone kryteria np. spełniały kryteria normalności rozkładu czy też rozciągały się w określonym przedziale.

Transformacja Boxa-Coxa
Transformacja Boxa-Coxa wprowadzona przez Boxa i Coxa w roku 1964¹⁾ sprowadza dane do rozkładu normalnego poprzez przekształcenie oparte na współczynniku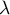 $\lambda$ . Do przeprowadzenia transformacji wymagane są dane dodatnie. Jeśli dane nie są dodatnie zaleca się ich wcześniejsze przekształcenie do liczb dodatnich metodą normalizacji min-max.

Transformacja Boxa-Coxa wyraża się wzorem:
$\begin{displaymath} x'=\left\{ \begin{array}{cl} \frac{x^\lambda-1}{\lambda} & $dla $ \lambda \neq 0\\ \ln(x) & $dla $\lambda = 0, \end{array}\right. \end{displaymath}$

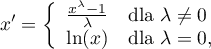
gdzie wartość 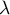$\lambda$ wyznaczana jest jako maksymalna wartość logartmu funkcji wiarygodności ( 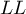$LL$ ) w podanym przez badacza przedziale. Domyślny przedział dla poszukiwania wartości 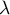$\lambda$ to przedział [-5, 5], a funkcja 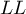$LL$ opisana jest wzorem:

$\begin{displaymath} LL=-\frac{n}{2}\ln(sd_{pop}^2)+(\lambda -1)\sum\ln x \end{displaymath}$

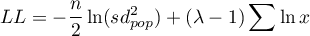
gdzie:
$n$ - liczność próby,
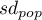$sd_{pop}$ - odchylenie standardowe populacji.

Uwaga! Jeśli przed transformacją Boxa-Coxa wykorzystano normalizację min-max, wówczas po transformacji Boxa-Coxa można powrócić do poprzedniego przedziału ponownie używając tej transformacji.

Transformacja logarytmiczna
Transformacja logarytmiczna może być wykorzystywana do redukcji skośności rozkładu tzn. w sytuacji gdy mamy do czynienia z rozkładem lognormalnym.
$\begin{displaymath} x'=\ln x \end{displaymath}$

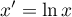
Standaryzacja
Standaryzacja, to przekształcenie danych, w wyniku którego zmienna uzyskuje średnią równą 0 a odchylenie standardowe równe 1.
$\begin{displaymath} x'=\frac{x-\bar{x}}{sd} \end{displaymath}$

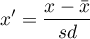
Rangowanie

Rangi - są to kolejne liczby (zwykle naturalne) przypisane do wartości uporządkowanych pomiarów badanej zmiennej. Często wykorzystywane są w tych testach nieparametrycznych, które bazują wyłącznie na kolejności elementów w próbie. Przypisanie do zmiennej wyliczonych według niej rang zwane jest rangowaniem. Rangowanie może odbywać się dla zmiennych sortowanych rosnąco (jest to domyślne ustawienie) lub malejąco.

Powtarzającym się wartościom zmiennej przypisuje się rangę wiązaną. Rangą wiązaną może być:
- średnia arytmetyczna wyliczana z proponowanych dla powtarzanych wartości kolejnych liczb naturalnych - jest to domyślne ustawienie;
- dolna granica, czyli najmniejsza z proponowanych dla powtarzanych wartości kolejnych liczb naturalnych;
- górna granica, czyli największa z proponowanych dla powtarzanych wartości kolejnych liczb naturalnych. ;. Taka ranga nazywana jest rangą wiązaną.

Na przykład dla zmiennej o następujących wartościach: 8.6, 5.3, 8.6, 7.1, 9.3, 7.2, 7.3, 7.4, 7.3, 5.2, 7, 9.9, 8.6, 5.7 przypisywane są następujące rangi:

$\begin{tabular}{|c|c|} \hline posortowane wartości zmiennej &rangi\\\hline 5.2 &1 \\ 5.3 &2 \\ 5.7 &3 \\ 7 &4 \\ 7.1 &5 \\ 7.2 &6 \\ 7.3 &7.5 \\ 7.3 &7.5 \\ 7.4 &9 \\ 8.6 &11 \\ 8.6 &11 \\ 8.6 &11 \\ 9.3 &13 \\ 9.9 &14 \\ \hline \end{tabular}$

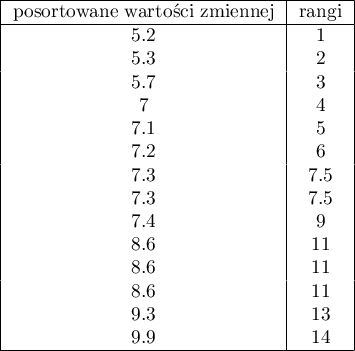
Przy czym dla zmiennej o wartości 7.3 przypisana jest ranga wiązana wyliczona z liczb: 7 i 8, a dla zmiennej o wartości 8.6 ranga wiązana wyliczona z liczb: 10, 11, 12.

Normalizacja min-max
Normalizacja min-max przy pomocy funkcji liniowej sprowadza dane do wskazanego przez użytkownika przedziału (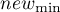 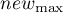$new_{\min}$ , $new_{\max}$ ). Powinniśmy przy tym znać zakres jaki mogą osiągnąć dane. Jeśli nie znamy tego zakresu, możemy posłużyć się wartością największą i najmniejszą występującą w analizowanym zbiorze (w oknie Transformacji zaznaczamy wtedy opcję oblicz z próby).
$\begin{displaymath} x'=\frac{x-\min}{\max-\min}\cdot(new_{\max}-new_{\min})+new_{\min} \end{displaymath}$

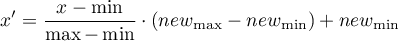
Normalizacja logistyczna
Normalizacja przy pomocy funkcji logarytmicznej (S-kształtnej) sprowadza dane zestandaryzowane do wskazanego przedziału.
$\begin{displaymath} x'=\frac{e^x}{1-e^x} \end{displaymath}$
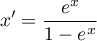
Jeśli tak przekształcone dane chcemy rozciągnąć na innym przedziale niż zadany, wówczas w oknie Transformacji należy wprowadzić zakres nowego przedziału.

Funkcja normalizująca ze współczynnikiem
Normalizacja ta sprowadza dane zestandaryzowane do wskazanego przedziału przy pomocy funkcji S-kształtnej o zmieniającym się współczynniku normalizacji $\alpha$ .
$\begin{displaymath} x'=\frac{x}{\sqrt{x^2+\alpha}} \end{displaymath}$
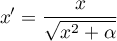
Zwiększenie wartości współczynnika $\alpha$ tworzy wykres o bardziej łagodnym zboczu.
Jeśli tak przekształcone dane chcemy rozciągnąć na innym przedziale niż zadany, wówczas w oknie Transformacji należy wprowadzić zakres nowego przedziału.

Kodowanie wielokrotnych odpowiedzi
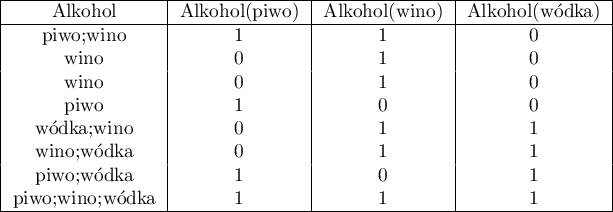
Ten rodzaj kodowania pozwala przygotować odpowiedzi udzielone na pytania wielokrotnego wyboru w taki sposób, by ułatwić ich dalszą obróbkę statystyczną. W efekcie zastosowania tej transformacji wybrana zmienna o k- możliwościach odpowiedziach jest rozbijana na k nowych zmiennych. Przy czym należy podać jaki znak (lub zestwa znaków) jest separatorem poszczególnych kategorii. Np. Zapytano ankietowanych jaki alkohol piją? Dane zapisano w kolumnie Alkohol oddzielając wielokrotne odpowiedzi znakiem średnika. Taki zapis danych nie pozwala nawet na proste podsumowanie. Nie można między innymi szybko zliczyć ile osób pije wino. Po przekodowaniu wielokrotnych odpowiedzi uzyskano trzy nowe kolumny - po jednej dla każdej z możliwych odpowiedzi. Każdą z tych kolumn można teraz poddać analizie statystycznej.

$\begin{tabular}{|c|c|c|c|} \hline Alkohol &Alkohol(piwo) &Alkohol(wino) & Alkohol(wódka)\\\hline piwo;wino &1 &1 &0 \\ wino &0 &1 &0 \\ wino &0 &1 &0 \\ piwo &1 &0 &0 \\ wódka;wino &0 &1 &1 \\ wino;wódka &0 &1 &1 \\ piwo;wódka &1 &0 &1 \\ piwo;wino;wódka &1 &1 &1 \\ \hline \end{tabular}$

Kodowanie zero-jedynkowe
Transformacja zmiennej o $k$ kategoriach poprzez kodowanie zero-jedynkowe pozwala na uzyskanie 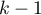$k-1$ zmiennych fikcyjnych. Taka forma przekształcania wykorzystywana jest przede wszystkim w modelach regresji. Dokładny opis tego typu transformacji można znaleźć w dziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych.
Kodowanie efektów
Transformacja zmiennej o $k$ kategoriach poprzez kodowanie efektów pozwala na uzyskanie 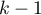$k-1$ zmiennych fikcyjnych. Taka forma przekształcania wykorzystywana jest przede wszystkim w modelach regresji i ANOVA. Dokładny opis tego typu transformacji można znaleźć w dziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych.
Podział na kategorie

Taki sposób przygotowania danych pozwala na dowolny podział zmiennych np. cholesterol całkowity możemy podzielić zgodnie z obowiązującymi normami (wówczas wybieramy podział Ręczny, ustawiamy liczbę kategorii i sami wpisujemy ich granice oraz nadajemy odpowiednie etykiety dla każdej kategorii). Jeśli jednak nie mamy gotowego pomysłu na podział naszych danych można skorzystać z zaproponowanych w oknie opcji podziału automatycznego. Możliwe sposoby podziału zmiennej:

- Naturalny Podział (Jenks) - metoda polegająca na takim podziale zmiennej na klasy, by zminimalizować wariancję w klasach a zmaksymalizować wariancję pomiędzy klasami.

- Podział według kwantyli - metoda polegająca na podziale zmiennej na klasy równej liczności.

- Odchylenie standardowe - metoda polegająca na podziale zmiennej na klasy w oparciu o oddalenie od średniej o 1, 2 lub więcej odchyleń standardowych.

- Błąd standardowy średniej - metoda polegająca na podziale zmiennej na klasy w oparciu o oddalenie od średniej o 1, 2 lub więcej błędów standardowych średniej.

- Ręczny - metoda polegająca na podziale zmiennej na klasy wg dowolnego podziału wprowadzonego ręcznie przez badacza.

W oknie podziału możliwe jest również wybranie opcji Dodaj schemat kolorów wówczas kolumna, która będzie przechowywała nowe dane zostanie oznaczona kolorami zgodnie ze wskazanym schematem

Zadanie (plik: normalizacja.pqs)

Dokonaj przekształcenia wszystkich zmiennych zawartych w pliku

a) Przekształć wartość trójglicerydów poprzez transformację Boxa-Coxa a następnie sprawdź przy pomocy odpowiedniego testu, czy dane te mają rozkład normalny.
b) Przekształć wartość trójglicerydów poprzez transformację logarytmiczną a następnie sprawdź przy pomocy odpowiedniego testu, czy dane te mają rozkład normalny.
c) Stosując normalizację min-max przekształć wybrane zmienne do przedziału [0,10].
d) Stosując normalizację logistyczną przekształć wybrane zmienne do zadanego przez siebie przedziału.
e) Stosując normalizację ze współczynnikiem przekształć wybrane zmienne do zadanego przez siebie przedziału. Zrób to kilkukrotnie zmieniając wartość współczynnika $\alpha$ .
f) Dokonaj standaryzacji wszystkich danych, które są opisane rozkładem normalnym.
g) Przekształć zmienną obrazującą jak zmieniła się masa ciała podczas stosowania diety tak, by przedstawiała ona rozkład normalny.
h) Pytanie o przebytych chorobach zakaźnych było pytaniem wielokrotnego wyboru. Przygotuj uzyskane odpowiedzi na to pytanie tak, by można było poddać je dalszej obróbce statystycznej tzn. zapisz każdą z wielokrotnych odpowiedzi w innej kolumnie.
i) Przygotuj zmienną wykształcenie tak, by była zapisana przy pomocy zmiennych fikcyjnych o kodowaniu zero-jedynkowym.
j) Przygotuj zmienną cholesterol całkowity dzieląc ją na 3 klasy wg podziału na percentyle (kwartyle). Powstałym klasom nadaj etykiety :„niski”, „przeciętny”, „wysoki” i dobierz schemat kolorów.

2014/08/22 20:00

Standaryzacja bezpośrednia i pośrednia

Okno bezpośredniej i pośredniej standaryzacji współczynników epidemiologicznych wywołujemy poprzez Dane→Standaryzacja…

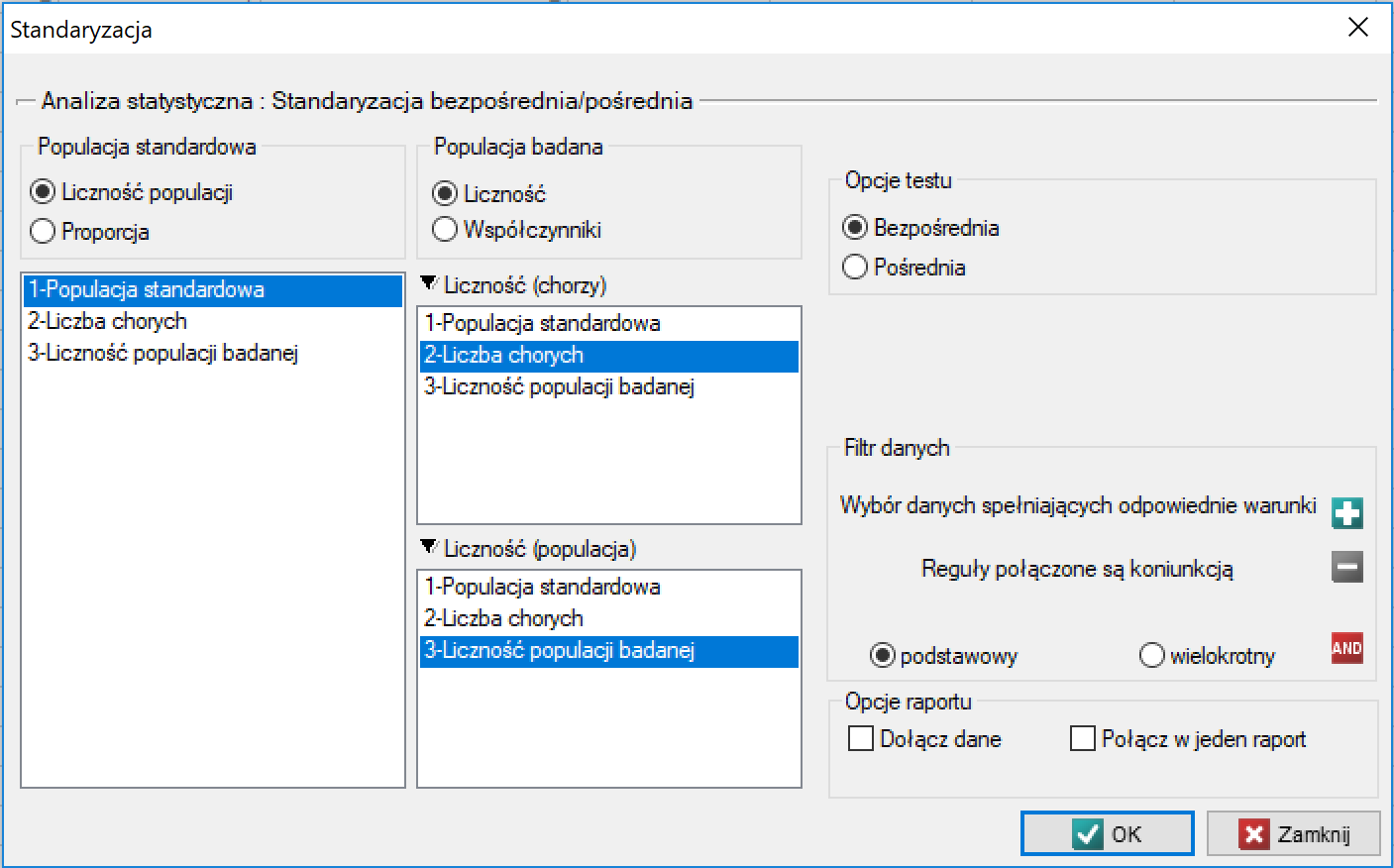
Standaryzacji pośredniej i bezpośredniej podlegają współczynniki częstość np. współczynniki chorobowości. Bezpośrednie porównanie surowych współczynników pomiędzy różnymi populacjami, zwykle zamieszkującymi rozmaite rejony geograficzne i różniącymi się czynnikami mogącymi wpływać na wartość współczynników (np. wiekiem), może maskować występujące różnice. By zniwelować wpływ struktury populacji co do tych cech wikłających, porównania można dokonać na bazie współczynników standaryzowanych. Standaryzacja oferuje mechanizm „odfiltrowania” wpływu znanego czynnika wikłającego (np. wieku) i czyni porównywalnymi współczynniki standaryzowane, uzyskane z różnych populacji. Niezbędnym etapem procesu standaryzacji współczynników jest wybór populacji standardowej. Populacją standardową dla populacji zajmującej określony obszar geograficzny w określonym czasie może być populacja obejmująca większy geograficznie obszar, w tym również obszar badany, np. jeśli populacją badaną jest populacja województwa wielkopolskiego, to populacja Polski może być wykorzystana jako populacja standardowa. Można również dokonać wyboru zupełnie innej populacji, odległej geograficznie od populacji badanej. Jednak dobrze jest, aby wybrana populacja stanowiła populację odniesienia nie tylko do przeprowadzanego właśnie badania, ale również dla wielu innych badaczy. Daje to bowiem możliwość porównania wyników badań z wykorzystaniem tej samej populacji standardowej. Wybierając populację, zaleca się zwrócenie uwagi na kilka aspektów dokonywane-go wyboru, m.in.:

jeśli kilka populacji jest porównywanych, wspólna populacja standardowa minimalizuje wariancję (zmienność) uzyskanych współczynników standardowych;
w analizie trendów polecaną populacją standardową jest populacja przedstawiająca średnią strukturę dla analizowanego odcinka czasu;
populacja standardowa powinna być jak najbardziej podobna do populacji badanej;
ta sama populacja standardowa powinna być konsekwentnie wybierana w celu zapewnienia porównywalności badań (wybór innej niż dotychczas używanej powszechnie populacji standardowej powoduje, iż wszystkie historyczne dane należałoby ponownie przeliczyć).

Wiek oraz płeć są najczęściej wykorzystywanymi cechami, względem których dokonuje się standaryzacji, niemniej standaryzacja może być dokonywana również w oparciu o inne, dowolne cechy, które ze względu na ich oczywisty wpływ na dane zjawisko warto „odfiltrować” z przeprowadzanego badania. Cechy takie nazywane są cechami zakłócającymi lub wikłającymi. Przy czym wybierając cechę, względem której chcemy dokonać standaryzacji, należy pamiętać, że standaryzacja będzie możliwa, jeśli mamy wystarczające informacje o rozkładzie tej cechy w populacji badanej i populacji standardowej (Tabela 1). Dodatkowo standaryzacja według wybranej cechy, np. według wieku, kompensuje w pewnym stopniu oddziaływanie innych czynników wikłających związanych z wiekiem, takich jak styl życia, a standaryzacja według płci kompensuje te czynniki, które są związane z płcią, np. wykonywane zawody. Kompensacja innych czynników jest więc ważnym aspektem przy doborze cechy, względem której dokonuje się standaryzacji.

Rodzaje standaryzacji:

standaryzacja bezpośrednia (ang. direct standardization) – uzyskany tą metodą standaryzowany współczynnik częstości podaje, jak wyglądałaby częstość występowania choroby w populacji badanej, gdyby posiadała ona strukturę (np. strukturę wiekową) populacji referencyjnej;
standaryzacja pośrednia (ang. indirect standardization) – uzyskany tą me-todą standaryzowany współczynnik częstości podaje, jak wyglądałaby czę-stość występowania choroby w populacji badanej, gdyby występowanie choroby w populacji badanej było takie samo w poszczególnych kategoriach (np. kategoriach wiekowych) jak w populacji referencyjnej.

2019/02/21 14:51 · admin

Symulacja próbkowania

Okno próbkowania wywołujemy poprzez Dane→Symulacja próbkowania …

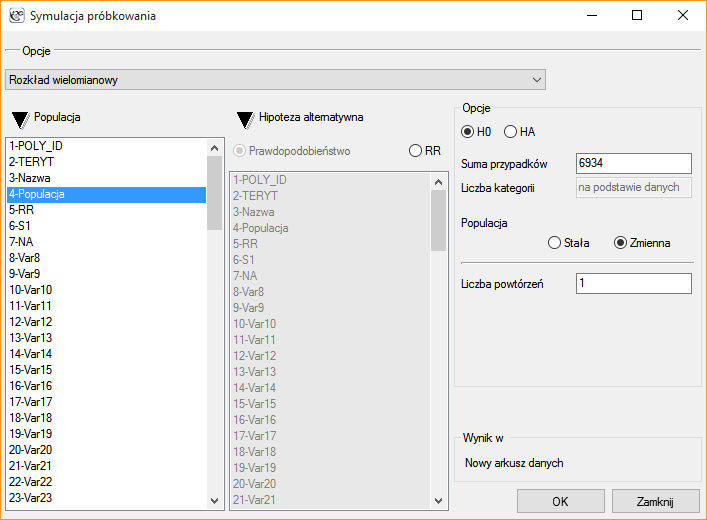
Symulacja próbkowania jest jednym ze sposobów generowania danych rozkładu wielomianowego. Polega na przydzieleniu podanej liczby przypadków do poszczególnych kategorii, w sposób zadany przez użytkownika. Wygenerowane dane zwracane są w nowym arkuszu. Generowanie może zostać powtórzone, tak by w arkuszu uzyskać wiele wygenerowanych kolumn w zależności od ustawionej w oknie próbkowania liczby powtórzeń tej operacji.

Opcje:

H0 - hipoteza zerowa zakłada równomierne rozmieszczenie wszystkich przypadków w poszczególnych kategoriach.
HA - hipoteza alternatywna zakłada nierównomierne rozmieszczenie przypadków. Wybranie tej opcji wymaga wskazania kategorii o większym prawdopodobieństwie lub relatywnym ryzyku. Informacja o zdefiniowanym prawdopodobieństwie lub relatywnym ryzyku dla każdej kategorii powinna zostać wprowadzona do wybranej kolumny arkusza przed przeprowadzeniem analizy.

Prawdopodobieństwo należy zdefiniować jako wartość od 0 do 1, przy czym suma prawdopodobieństw podanych dla wszystkich kategorii powinna wynosić 1.

Relatywne ryzyko definiuje ryzyko względem innych kategorii i dla kategorii o zwiększonym ryzyku jest wartością większą niż 1, a ułamkiem mniejszym niż 1 dla kategorii o zmniejszonym ryzyku.

Ustawienie wartości prawdopodobieństwa lub relatywnego ryzyka na tym samym poziomie dla wszystkich kategorii, tożsame jest z rozkładem dla H0.

Populacja stała - zakłada, że użytkownik zainteresowany jest rozmieszczeniem przypadków zgodnie z zaproponowanym rozkładem.
Populacja zmienna - zakłada, że użytkownik zainteresowany jest takim rozmieszczeniem przypadków, aby proporcja przypadków do populacji rozmieszczona została zgodnie z zaproponowanym rozkładem.

Przykład (plik symulacje.pqs)

Jako podstawę symulacji użyto populację Wielkopolski w roku 2013, która wynosiła wg GUS $N$ = 3467016 osób. Województwo podzielone jest na 315 gmin. Gminy różnią się znacznie liczbą mieszkańców. Najliczniejsza gmina (stolica województwa) 548028 mieszkańców, najmniej liczna 1454 mieszkańców, mediana i kwartyle to odpowiednio: 6298 (4462; 9621) mieszkańców. Przy założeniu, że w 2013 roku mieszkańców województwa z chorobą X było 6934, należy zasymulować rozlokowanie osób chorych w taki sposób, by uzyskać:

Rozkład losowy (na podstawie danych z arkusza „Losowy”)
Czterokrotnie większe częstości występowania choroby we wskazanych gminach niż w pozostałej części województwa (na podstawie danych z arkusza „Klastery”)

[Ad 1.]

Należy zaznaczyć, że równomierne rozłożenie 6934 chorych w sposób losowy nie oznacza podobnej liczby chorych w każdej gminie. Wiadomo, że gminy o większej liczbie narażonych powinny mieć odpowiednią większą liczbę chorych niż te o mniejszej liczbie mieszkańców. Interesujące jest więc takie rozłożenie chorych, by współczynnik liczby chorych do liczby mieszkańców był względnie stały. Oznacza to przyjęcie hipotezy zerowej H0 i zmiennej populacji. Liczność poszczególnych gmin zapisano w kolumnie o nazwie: populacja.

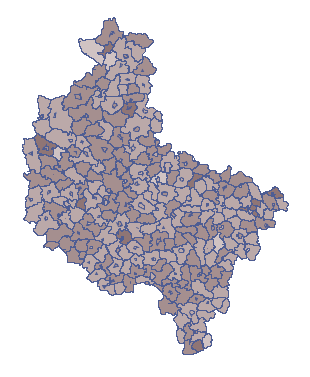
Wylosowane na podstawie tych założeń dane przedstawiono w pierwszej kolumnie nowego arkusza danych. By móc obserwować losowy rozkład współczynnika chorych w poszczególnych gminach, należy przekopiować uzyskany wynik do arkusza „Losowo” kolumny „S1”. Formuła znajdująca się w kolumnie 7 zostanie wówczas ponownie przeliczona (podejrzeć i zmienić formułę można ustawiając Kody/Etykiety/Format we właściwościach kolumny). Na mapie przedstawiamy uzyskany wynik przy pomocy menagera Map z menu Analiza przestrzenna. Wyrysowana zostaje wówczas proporcja chorych do liczby mieszkańców w poszczególnych gminach. Przykładowy wynik przedstawia poniższa mapa.

[Ad 2.]

W arkuszu „Klastery” podano, podobnie jak w poprzednim zadaniu, liczność dla populacji badanej. Tym razem oczekujemy wyższej częstości w niektórych gminach (wskazanych na mapie) więc dodatkowo w kolejnej kolumnie arkusza przedstawiono wartość relatywnego ryzyka dla poszczególnych gmin ustawiając ją na 4, dla gmin zwiększonego ryzyka i 1 dla pozostałych gmin.

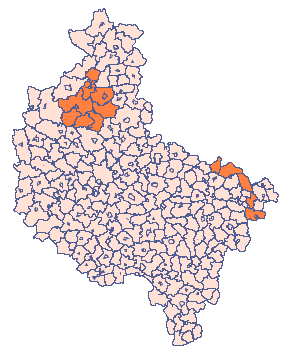
Odpowiednie próbkowanie wymaga od nas wybrania hipotezy alternatywnej HA (poprzez wybranie kolumny z relatywnym ryzykiem) i zmiennej populacji (poprzez wskazanie kolumny z licznością populacji gmin). Wylosowane na podstawie tych założeń dane przedstawiono w pierwszej kolumnie nowego arkusza danych.

By móc obserwować rozkład współczynnika, przy założeniu większego ryzyka we wskazanych gminach, należy przekopiować uzyskany wynik do arkusza „Klastery” kolumny „S1”. Formuła znajdująca się w kolumnie 7 zostanie wówczas ponownie przeliczona. Na mapie przedstawiamy uzyskany wynik przy pomocy menagera Map z menu Analiza przestrzenna. Wyrysowana zostaje wówczas proporcja chorych do liczby mieszkańców w poszczególnych gminach. Przykładowy wynik przedstawia poniższa mapa.

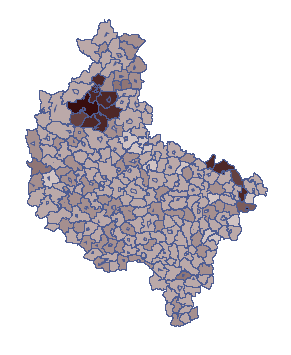
2015/12/27 22:34 · admin

Macierz podobieństwa

Wzajemne relacje między obiektami mogą być wyrażone przez ich odległości lub bardziej ogólnie poprzez niepodobieństwo. Czym dalej od siebie znajdują się obiekty, tym bardziej są do siebie niepodobne, im bliżej natomiast, tym podobieństwo między nimi jest większe. Badać można odległość obiektów pod względem wielu cech np. gdy porównywane obiekty to miasta ich podobieństwo możemy definiować między innymi w oparciu o: długość drogi je łączącej, gęstości zaludnienia, PKB przypadającym na mieszkańca, emisję zanieczyszczeń, przeciętne ceny nieruchomości itd. Mając tak wiele różnych cech badacz tak musi dobrać miarę odległości, by najlepiej obrazowała rzeczywiste podobieństwo obiektów.

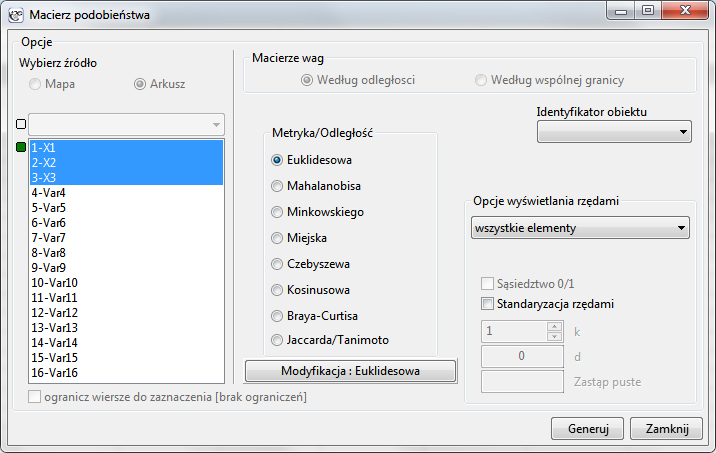
Okno z ustawieniami opcji macierzy podobieństwa wywołujemy poprzez menu Dane→Macierz podobieństwa…

Niepodobieństwo/podobieństwo obiektów wyrażamy za pomocą odległości będących najczęściej metryką. Nie każda miara odległości jest jednak metryką. Aby odległość mogła być nazwana metryką musi spełniać 4 warunki:

odległość pomiędzy obiektami nie może być ujemna: $d(x_1, x_2) \geq 0$ ,
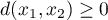odległość między dwoma obiektami wynosi 0 wtedy i tylko wtedy gdy są one identyczne: $d(x_1, x_2) = 0 \Longleftrightarrow x_1 = x_2$ ,
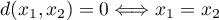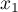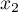odległość musi być symetryczna, tzn. odległość z obiektu $x_1$ do $x_2$ musi być taka sama jak z 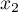$x_2$ do $x_1$ : $d(x, y) = d(y, x)$ ,
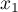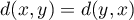odległość musi spełniać warunek trójkąta: $d(x, z) \leq (x, y) + d(y, z)$ .

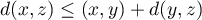Uwaga!
Metryki powinny być wyliczane dla cech o tych samych zakresach wartości. Gdyby tak nie było to cechy o wyższych zakresach miałyby większy wpływ na uzyskany wynik podobieństwa niż te o niższych zakresach. Przykładowo, wyliczając podobieństwo osób możemy oprzeć je na takich cechach jak min. masa ciała i wiek. Wówczas masa ciała w kilogramach, w zakresie od 40 do 150 kg, będzie miała większy wpływ na wynik niż wiek w latach, w zakresie od 18 do 90 lat. By wpływ każdej cechy na uzyskany wynik podobieństwa był zrównoważony powinniśmy każdą z nich znormalizować/wystandaryzować przed przystąpieniem do analizy. Chcąc natomiast samodzielnie zdecydować o wielkości tego wpływu, po zastosowaniu standaryzacji, wskazując rodzaj metryki należy wpisać nadane przez siebie wagi.

Odległość/Metryka:

Euklidesowa
Kiedy mówimy o odległości nie definiując jej rodzaju zakładamy, że jest to odległość Euklidesowa - najpopularniejszy typ odległości stanowiący naturalny element modeli świata rzeczywistego. Odległość euklidesowa jest metryką i dana jest wzorem:
$\begin{displaymath} d(x_1,x_2)=\sqrt{\sum_{k=1}^n\left(x_{1k}-x_{2k}\right)^2} \end{displaymath}$

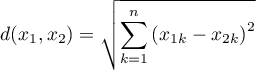
Minkowskiego
Odległość Minkowskiego definiowana jest dla parametrów $p$ i $r$ równych sobie - jest wówczas metryką. Ten rodzaj metryki pozwala sterować procesem wyliczania podobieństwa poprzez podanie wartości $p$ i $r$ ujętymi we wzorze:
$\begin{displaymath} d(x_1,x_2)=\sqrt[p]{\sum_{k=1}^n\left|x_{1k}-x_{2k}\right|^r} \end{displaymath}$
Zwiększając parametr $r$ zwiększamy wagę przypisaną różnicy pomiędzy obiektami dla każdej cechy, zmieniając $p$ nadajemy większe/mniejsze znaczenie obiektom bliższym/dalszym. Jeśli $r$ i $p$ są równe 2, to odległość Minkowskiego sprowadza się do odległości Euklidesowej, jeśli są równe 1, do odległości Miejskiej, a przy tych parametrach dążących do nieskończoności, do metryki Czebyszewa.

Miejska (inaczej: odległość Manhattan lub odległość taksówkowa)
To odległość pozwalająca na poruszanie się tylko w dwóch prostopadłych do siebie kierunkach. Ten rodzaj odległości przypomina poruszanie się po prostopadle przecinających się ulicach (kwadratowa sieć ulic przypominająca plan Manhattanu). Metryka ta dana jest wzorem:
$\begin{displaymath} d(x_1,x_2)=\sum_{k=1}^n|x_{1k}-x_{2k}| \end{displaymath}$

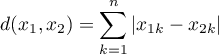
Czebyszewa
Odległość pomiędzy porównywanymi obiektami to największa z uzyskanych odległości dla poszczególnych cech tych obiektów:
$\begin{displaymath} d(x_1,x_2)=\max_{k}|x_{1k}-x_{2k}| \end{displaymath}$

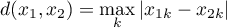
Mahalanobisa
Odległość Mahalanobisa nazywana jest również odległością statystyczną. Jest to odległość ważona macierzą kowariancji, przez co porównywać można obiekty opisane wzajemnie skorelowanymi cechami. Stosowanie odległości Mahalanobisa daje dwie podstawowe korzyści:
1) Zmienne, dla których obserwowane są większe odchylenia lub większe zakresy wartości nie mają zwiększonego wpływu na wynik odległości Mahalanobisa (stosując macierz kowariancji standaryzujemy bowiem zmienne wykorzystując wariancję znajdującą się na diagonali). W rezultacie przed przystąpieniem do analizy nie ma wymogu standaryzowania/normalizacji zmiennych.
2) Bierze pod uwagę wzajemne skorelowanie cech opisujących porównywane obiekty (stosując macierz kowariancji wykorzystujemy informację o zależności między cechami znajdującą się poza przekątną macierzy).
$\begin{displaymath} d(x_1,x_2)=\sqrt{(\vec{x}-\vec{y})^TS^{-1}(\vec{x}-\vec{y})} \end{displaymath}$
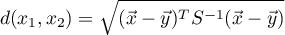
Wyliczona w ten sposób miara spełnia warunki metryki.

Kosinusowa
Odległość kosinusowa powinna być wyliczana na danych dodatnich ponieważ nie jest ona metryką (nie spełnia pierwszego warunku: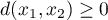 $d(x_1, x_2) \geq 0$ ). Jeśli więc mamy cechy przyjmujące również wartości ujemne powinnyśmy je wcześniej przekształcić stosując np. normalizację do przedziału rozpiętego na liczbach dodatnich. Zaletą tej odległości jest fakt, że (dla dodatnich argumentów) ograniczona jest do przedziału [0, 1]. Podobieństwo dwóch obiektów reprezentuje kąt pomiędzy dwoma wektorami przedstawiającymi cechy tych obiektów.
$\begin{displaymath} d(x_1,x_2)=1-K, \end{displaymath}$
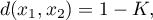
Gdzie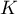 $K$ to współczynnik podobieństwa (kosinus kąta pomiędzy dwoma znormalizowanymi wektorami):
$\begin{displaymath} K=\frac{\sum_{k=1}^nx_{1k}x_{2k}}{\sqrt{\sum_{k=1}^nx_{1k}^2}\sqrt{\sum_{k=1}^nx_{2k}^2}} \end{displaymath}$
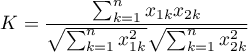
Obiekty są podobne, gdy wektory się pokrywają - wtedy kosinus kąta (podobieństwo) wynosi 1 odległość (niepodobieństwo) 0. Obiekty są różne, gdy wektory są prostopadłe - wtedy kosinus kąta (podobieństwo) wynosi 0 odległość (niepodobieństwo) wynosi 1.

Przykład - porównanie tekstów
Tekst 1: na tym przystanku wsiadło kilka osób a na następnym wysiadła jedna
Tekst 2: na przystanku jedna Pani wysiadła a kilka wsiadło
Chcemy wiedzieć, jak podobne są teksty pod względem liczby tych samych słów, nie interesuje nas natomiast kolejność występowania słów.
Tworzymy listę słów z obu tekstów i liczymy jak często wystąpiło każde słowo:

$\begin{tabular}{|c||c|c|c|c|c|c|c|c|c|c|c|c|} \hline \textbf{SŁOWA}&na&tym&przystanku&wsiadło&kilka&osób&a&następnym&wysiadła&jedna&Pani\\ \hline \textbf{tekst 1}&2&1&1&1&1&1&1&1&1&1&0\\ \textbf{tekst 2}&1&0&1&1&1&0&1&0&1&1&1\\\hline \end{tabular}$

Kosinus kąta pomiędzy wektorami wynosi 0,784465, a więc odległość miedzy nimi nie jest duża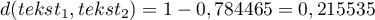 $d(tekst_1,tekst_2)=1-0,784465=0,215535$ .
Na podobnej zasadzie możemy porównywać dokumenty pod względem występowania słów kluczowych, tak by znajdować te najbardziej odpowiadające zapytaniu.

Braya-Curtisa
Odległość (miara niepodobieństwa) Bray'a-Curtis'a powinna być wyliczana na danych dodatnich ponieważ nie jest ona metryką (nie spełnia pierwszego warunku: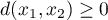 $d(x_1, x_2) \geq 0$ ). Jeśli mamy cechy przyjmujące również wartości ujemne, powinnyśmy je wcześniej przekształcić stosując np. normalizację do przedziału rozpiętego na liczbach dodatnich. Zaletą tej odległości jest fakt, że (dla dodatnich argumentów) ograniczona jest do przedziału [0, 1], gdzie 0 - oznacza, że porównywane obiekty są podobne, 1 - niepodobne.
$\begin{displaymath} d(x_1,x_2)=\frac{\sum_{k=1}^n|x_{1k}-x_{2k}|}{\sum_{k=1}^n(x_{1k}+x_{2k})} \end{displaymath}$
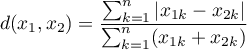
Wyliczając miarę podobieństwa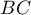 $BC$ od wartości 1 odejmujemy odległość Bray'a-Curtis'a:
$\begin{displaymath} BC=1-d(x_1,x_2) \end{displaymath}$

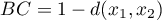
Jaccarda
Odległość (miara niepodobieństwa) Jaccarda wyliczana jest dla zmiennych binarnych (Jaccard, 1901), gdzie 1 oznacza występowanie danej cech 0- jej brak.

$\begin{tabular}{|c|c||c|c|} \hline \multicolumn{2}{|c||}{ }& \multicolumn{2}{|c|}{objekt 1} \cline{3-4} \multicolumn{2}{|c||}{ }& 1 & 0 \\ \hline \hline \multirow{}{}{objekt 2}& 1 & a & b \\ \cline{2-4} & 0 & c & d\\ \hline \end{tabular}$

Odległość Jacckarda wyraża się wzorem:
$\begin{displaymath} d(x_1,x_2)=1-J. \end{displaymath}$
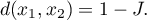
gdzie:

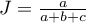$J=\frac{a}{a+b+c}$ - współczynnik podobieństwa Jaccarda.

Współczynnik podobieństwa Jaccarda zawiera się w przedziale [0,1], gdzie 1 oznacza najwyższe podobieństwo, 0 - najniższe. Odległość (niepodobieństwo) interpretujemy przeciwnie: 1 - oznacza, że porównywane obiekty są niepodobne, 0 - że bardzo podobne.
Sens współczynnika podobieństwa Jaccarda dobrze opisuje sytuacja dotycząca wyboru towaru przez klientów. Przez 1 oznaczymy fakt zakupu danego produktu przez klienta, 0 - klient nie kupił tego artykułu. Wyliczając współczynnik Jaccarda porównamy 2 produkty by dowiedzieć się jaka część klientów kupuje je w tandemie. Nie interesuje nas oczywiście informacja o klientach, którzy nie kupili żadnego z porównywanych artykułów. Jesteśmy natomiast ciekawi jak wiele osób wybierających jeden z porównywanych produktów wybiera jednocześnie ten drugi. Suma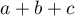 $a+b+c$ - to liczba klientów, którzy wybrali któryś z porównywanych artykułów, 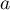$a$ - to liczba klientów wybierających oba artykuły jednocześnie. Im wyższy współczynnik podobieństwa Jaccarda, tym bardziej nierozerwalne są artykuły (zakupowi jednego towarzyszy zakup drugiego). Odwrotnie będzie, gdy dostaniemy wysoki współczynnik niepodobieństwa Jaccarda. Będzie on świadczył o dużej konkurencyjności artykułów, tzn. zakup jednego będzie powodował brak zakupu drugiego.
Wzór na współczynnik podobieństwa Jaccarda można również zapisać w ogólnej postaci:

$J=\frac{\sum_{k=1}^nx_{1k}x_{2k}}{\sum_{k=1}^nx_{1k}^2\sum_{k=1}^nx_{2k}^2-\sum_{k=1}^nx_{1k}x_{2k}}$

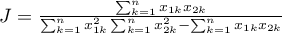
zaproponowanej przez Tanimoto (1957). Ważną cechą formuły Tanimoto jest fakt, że może być wyliczana także dla cech ciągłych.
W przypadku danych binarnych wzory na niepodobieństwo/podobieństwo Jaccarda i Tanimoto są tożsame i spełniają warunki metryki. Natomiast dla zmiennych ciągłych wzór Tanimoto nie jest metryką (nie spełnia warunku trójkąta).

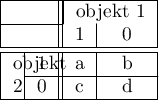
Przykład - porównanie gatunków
Badamy podobieństwo pod względem genetycznym przedstawicieli trzech różnych gatunków - w sensie ilości genów które są dla nich wspólne. Jeśli gen występuje w organizmie, to dajemy mu wartość 1, 0 - w przeciwny przypadku. Dla prostoty przykładu analizie poddanych jest zaledwie 10 genów.

$\begin{tabular}{|c||c|c|c|c|c|c|c|c|c|c|} \hline \textbf{GENY}&gen1&gen2&gen3&gen4&gen5&gen6&gen7&gen8&gen9&gen10\\ \hline \textbf{osobnik1}&0&1&1&1&1&1&1&0&1&0\\ \textbf{osobnik2}&0&0&1&1&1&1&1&0&1&0\\ \textbf{osobnik3}&1&0&1&1&0&0&1&0&0&0\\ \hline \end{tabular}$

Wyliczona macierz podobieństwa przedstawia się następująco:

$\begin{tabular}{|c||c|c|c|} \hline \textbf{OBIEKTY}&osobnik1&osobnik2&osobnik3\\ \hline \textbf{osobnik1}&0&0.857143&0.375\\ \textbf{osobnik2}&0.857143&0&0.428571\\ \textbf{osobnik3}&0.375&0.428571&0\\ \hline \end{tabular}$

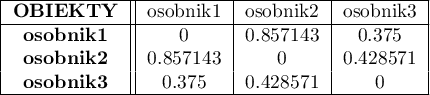
Najbardziej podobni są osobnicy 1 i 2 a najmniej 1 i 3:
- podobieństwo Jaccarda osobnika1 i osobnika2 wynosi 0.857143, czyli nieco ponad 85% genów występujących w obu porównywanych gatunkach jest dla nich wspólna.
- podobieństwo Jaccarda osobnika1 i osobnika3 wynosi 0.375, czyli ponad 37% genów występujących w obu porównywanych gatunkach jest dla nich wspólna.
- podobieństwo Jaccarda osobnika2 i osobnika3 wynosi 0.428571, czyli prawie 43% genów występujących w obu porównywanych gatunkach jest dla nich wspólna.

Opcje macierzy podobieństwa
wykorzystujemy do wskazania sposobu zwracania elementów w macierzy. Standardowo zwracane są wszystkie elementy macierzy, w takiej formie w jakiej były wyliczone zgodnie z przyjętą metryką. Możemy to zmienić ustawiając:

Elementy macierzy:
- minimum - oznacza, że w każdym wierszu macierzy zostanie wyświetlona tylko wartość minimalna i wartość na głównej przekątnej;
- maksimum - oznacza, że w każdym wierszu macierzy zostanie wyświetlona tylko wartość maksymalna i wartość na głównej przekątnej;
- $k$ minimalnych - oznacza, że w każdym wierszu macierzy zostanie wyświetlonych tyle najmniejszych wartości ile wskaże użytkownik podając wartość $k$ oraz wartość na głównej przekątnej;
- $k$ maksymalnych - oznacza, że w każdym wierszu macierzy zostanie wyświetlonych tyle największych wartości ile wskaże użytkownik podając wartość $k$ oraz wartość na głównej przekątnej;
- elementy poniżej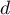 $d$ - oznacza, że w każdym wierszu macierzy zostaną wyświetlone te elementy, których wartość będzie mniejsza niż wskazana przez użytkownika wielkość 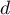$d$ oraz wartość na głównej przekątnej;
- elementy powyżej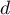 $d$ - oznacza, że w każdym wierszu macierzy zostaną wyświetlone te elementy, których wartość będzie większa niż wskazana przez użytkownika wielkość 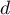$d$ oraz wartość na głównej przekątnej;
Sąsiedztwo 0/1
Wybierając opcję Sąsiedztwo 0/1 wartości wewnątrz macierzy zastępujemy wartością 1, a miejsca puste wartością 0. W ten sposób oznaczamy na przykład czy obiekty sąsiadują (1) czy nie (0), czyli wyznaczamy macierz sąsiedztwa.
Standaryzacja rzędami
Standaryzacja rzędami oznacza, że każdy element macierzy dzielony jest przez sumę wiersza macierzy. W rezultacie uzyskane wartości znajdują się w przedziale od 0 do 1.
Zastąp puste
Opcja Zastąp puste pozwala na wpisanie wartości jaka ma zostać umieszczona w macierzy w miejscu ewentualnych pustych elementów.
Wybrany identyfikator obiektu pozwala nazwać wiersze i kolumny macierzy podobieństwa zgodnie z nazewnictwem przechowywanym we wskazanej zmiennej.

Przykład (plik: podobienstwoLokali.pqs)

W procedurach wyceny nieruchomości, zarówno ze względów merytorycznych jak też prawnych, kwestia podobieństwa pełni ważną rolę. Jest na przykład zasadniczą przesłanką umożliwiającą grupowanie obiektów i przypisywanie do odpowiedniego segmentu.

Załóżmy, że do pośrednika nieruchomości zgłasza się osoba poszukująca mieszkania, która definiuje te cechy, które lokal musi posiadać i te, które mają duży wpływ na decyzję o zakupie ale nie są decydujące. Cechy, które lokal musi posiadać to:

nieruchomość lokalowa (stanowiąca przedmiot odrębnej własności),
położona w dzielnicy A,
położona w niskiej zabudowie wielorodzinnej (do 5-ciu kondygnacji),
nie remontowana (standard przeciętny lub pogorszony).

Dane dotyczące tych lokali zebrano w tabeli, gdzie 1 oznacza, że lokal spełnia warunki wyszukiwania, 0 że ich nie spełnia.

Te lokale, które nie spełniają warunków wyszukiwania wyłączymy z analizy poprzez dezaktywację odpowiednich wierszy. Poprzez menu Edycja→Aktywuj/Dezaktywuj (filtr)… dezaktywujemy te wiersze, które nie spełniają choćby jednego z postawionych warunków.

Pamiętamy by warunki dezaktywacji połączone były alternatywą (zmieniamy na ).

W rezultacie wyłoniono 11 lokali (lokal 10, 12, 17, 35, 88, 101, 105, 122, 130, 132, 135) pasujących do tego segmentu (spełniających wszystkie 4 warunki).

Teraz weźmiemy pod uwagę te cechy, które mają duży wpływ na decyzję klienta, ale nie są decydujące:

Liczba pokoi = 3;
Piętro na którym znajduje się lokal = 0;
Wiek budynku w którym znajduje się lokal = ok. 3 lata;
Bliskość centrum dzielnicy A (czas jaki zajmuje dotarcie do centrum) = ok. 30 min;
Bliskość przystanku komunikacji miejskiej = ok. 80 m.

$\begin{tabular}{|c||c|c|c|c|c|} \hline &\textbf{Liczba}&\textbf{Piętro}&\textbf{Wiek}&\textbf{Dystans}&\textbf{Odległość}\\ &\textbf{pokoi}&\textbf{lokalu}&\textbf{budynku}&\textbf{do centrum}&\textbf{przystanku}\\\hline\hline \rowcolor[rgb]{0.75,0.75,0.75}Poszukiwany&3&0&3&30&80\\ Lokal 10&2&1&1&0&150\\ Lokal 12&1&2&1&0&200\\ Lokal 17&3&1&7&20&500\\ Lokal 35&2&0&6&5&100\\ Lokal 88&3&4&6&5&200\\ Lokal 101&4&2&10&0&10\\ Lokal 105&2&2&6&0&50\\ Lokal 122&1&0&6&5&100\\ Lokal 130&2&0&10&0&20\\ Lokal 132&3&5&6&30&400\\ Lokal 135&3&1&6&5&100\\ \hline \end{tabular}$

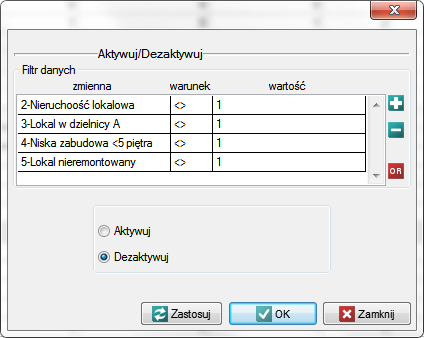
Zauważmy, że ostatnia cecha, czyli odległość przystanku komunikacji miejskiej jest wyrażona znacznie większymi liczbami niż pozostałe cechy porównywanych lokali. W rezultacie cecha ta będzie miała znacznie większy wpływ na uzyskany wynik macierzy odległości niż pozostałe cechy. Chcąc temu zapobiec przed analizą normalizujemy wszystkie cechy wybierając dla nich wspólny zakres od 0 do 1 - w tym celu korzystamy z menu Dane→Normalizacja/Standaryzacja…. W oknie normalizacji jako zmienną wejściową ustawiamy „Liczbę pokoi”, a jako zmienną wyjściową pustą zmienną nazwaną „Norm(Liczba pokoi)”; rodzaj normalizacji to normalizacja min/max; wartości min i max wyliczamy z próby wybierając przycisk Oblicz z próby - wynik normalizacji zostanie zwrócony do arkusza danych po wybraniu przycisku Wykonaj. Normalizację powtarzamy dla kolejnych zmiennych czyli: „Piętra”, „Wieku budynku”, „Dystansu do centrum” i „Odległości przystanku”.

Znormalizowane dane przedstawia poniższa tabela.

$\begin{tabular}{|c||c|c|c|c|c|} \hline &\footnotesize{\textbf{Norm(Liczba}}&\footnotesize{\textbf{Norm(Piętro}}&\footnotesize{\textbf{Norm(Wiek}}&\footnotesize{\textbf{Norm(Dystans}}&\footnotesize{\textbf{Norm(Odległość}}\\ &\footnotesize{\textbf{pokoi)}}&\footnotesize{\textbf{lokalu)}}&\footnotesize{\textbf{budynku)}}&\footnotesize{\textbf{do centrum)}}&\footnotesize{\textbf{przystanku)}}\\\hline \rowcolor[rgb]{0.75,0.75,0.75}Poszukiwany&0,666666667&0&0,222222222&1&0,142857143\\ Lokal 10&0,333333333&0,2&0&0&0,285714286\\ Lokal 12&0&0,4&0&0&0,387755102\\ Lokal 17&0,666666667&0,2&0,666666667&0,666666667&1\\ Lokal 35&0,333333333&0&0,555555556&0,166666667&0,183673469\\ Lokal 88&0,666666667&0,8&0,555555556&0,166666667&0,387755102\\ Lokal 101&1&0,4&1&0&0\\ Lokal 105&0,333333333&0,4&0,555555556&0&0,081632653\\ Lokal 122&0&0&0,555555556&0,166666667&0,183673469\\ Lokal 130&0,333333333&0&1&0&0,020408163\\ Lokal 132&0,666666667&1&0,555555556&1&0,795918367\\ Lokal 135&0,666666667&0,2&0,555555556&0,166666667&0,183673469\\ \hline \end{tabular}$

Bazując na danych znormalizowanych wyznaczymy lokale najbardziej dopasowane do zapytania klienta. Do wyliczenia podobieństwa posłużymy się metryką (odległością) euklidesową. Czym mniejszą uzyskamy wartość, tym bardziej podobne będą lokale. Analizę przeprowadzić można zakładając, że każda z pięciu wymienionych przez klienta cech jest tak samo ważna, ale można również wskazać te cechy, które powinny w większym stopniu wpływać na wynik analizy. Zbudujemy dwie macierze odległości euklidesowych:

W pierwszej macierzy znajdą się odległości euklidesowe wyliczone na podstawie równoważnie traktowanych pięciu cech;
W drugiej macierzy znajdą się odległości euklidesowe, w budowie których największe znaczenie będzie miała liczba pokoi i dystans do centrum dzielnicy.

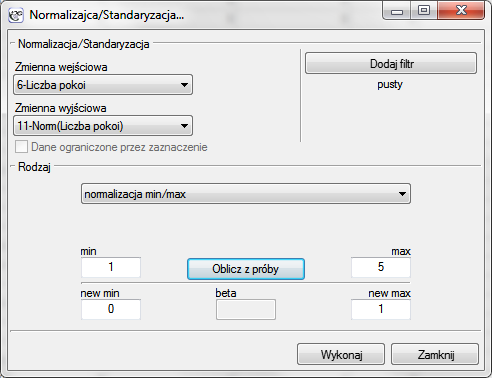
By zbudować pierwszą macierz, w oknie macierzy podobieństwa wybieramy 5 znormalizowanych zmiennych oznaczonych jako Norm, metrykę Euklidesową i jako Identyfikator obiektu zmienną „Lokal”.

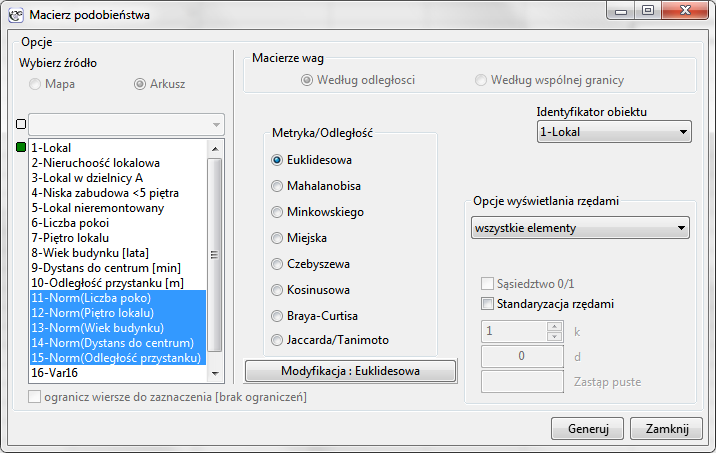
By zbudować drugą macierz, w oknie macierzy podobieństwa dokonujemy tych samych ustawień co przy budowie pierwszej macierzy, ale dodatkowo wybieramy przycisk Modyfikacja : Euklidesowa i w oknie modyfikacji wpisujemy większe wagi dla „Liczby pokoi” i „Dystansu do centru” np. równe 10, a mniejsze dla pozostałych cech np. równe 1.

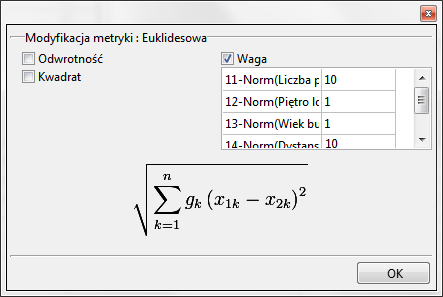
W rezultacie uzyskamy dwie macierze. W każdej z nich pierwsza kolumna dotyczy podobieństwa do lokalu szukanego przez klienta:

$\begin{tabular}{|c||c|c|} \hline Euklidesowa&\textbf{Poszukiwany}&...\\\hline \rowcolor[rgb]{0.75,0.75,0.75}Poszukiwany&0&...\\ Lokal 10&1.10&...\\ Lokal 12&1.31&...\\ Lokal 17&1.04&...\\ Lokal 35&\textcolor[rgb]{0,0,1}{0.96}&...\\ Lokal 88&1.23&...\\ Lokal 101&1.38&...\\ Lokal 105&1.18&...\\ Lokal 122&1.12&...\\ Lokal 130&1.32&...\\ Lokal 132&1.24&...\\ Lokal 135&\textcolor[rgb]{0,0,1}{0.92}&...\\ \hline \end{tabular}$

$\begin{tabular}{|c||c|c|} \hline Euklidesowa z wagami&\textbf{Poszukiwany}&...\\\hline \rowcolor[rgb]{0.75,0.75,0.75}Poszukiwany&0&...\\ Lokal 10&3.35&...\\ Lokal 12&3.84&...\\ Lokal 17&\textcolor[rgb]{0,0,1}{1.44}&...\\ Lokal 35&2.86&...\\ Lokal 88&2.78&...\\ Lokal 101&3.45&...\\ Lokal 105&3.37&...\\ Lokal 122&3.39&...\\ Lokal 130&3.43&...\\ Lokal 132&\textcolor[rgb]{0,0,1}{1.24}&...\\ Lokal 135&2.66&...\\ \hline \end{tabular}$

Według niemodyfikowanej odległości euklidesowej warunkom klienta najbardziej odpowiadać powinien lokal 35 i lokal 135. Gdy uwzględnimy wagi, najbardziej zbliżonymi do wymogów klienta będą lokale 17 i 132 - są to lokale, które w pierwszej kolejności są podobne pod względem wymaganej przez klienta liczby pokoi (3) i wskazanej odległości do centrum, mniejszy wpływ na wynik tego podobieństwa mają 3 pozostałe cechy.

2014/08/22 20:00

¹⁾

Box G. E. , Cox D. R. (1964), An analysis of transformations. Journal of the Royal Statistical Society, Series B 26: 211–252

PQStat - Baza Wiedzy

Pasek boczny

Spis treści

Working with datasheets

Dodawanie, usuwanie i eksport

Umieszczanie danych

Import danych

Okno arkusza

Właściwości zmiennej

Format komórek

Edycja danych

Sortowanie danych

Zamiana danych surowych na tabelę kontyngencji

Zamiana tabeli kontyngencji na dane surowe

Formuły

Generowanie danych

Braki danych

Transformacja

Standaryzacja bezpośrednia i pośrednia

Symulacja próbkowania

Macierz podobieństwa

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Spis treści

Working with datasheets

Dodawanie, usuwanie i eksport

Umieszczanie danych

Import danych

Okno arkusza

Właściwości zmiennej

Format komórek

Edycja danych

Sortowanie danych

Zamiana danych surowych na tabelę kontyngencji

Zamiana tabeli kontyngencji na dane surowe

Formuły

Generowanie danych

Braki danych

Transformacja

Standaryzacja bezpośrednia i pośrednia

Symulacja próbkowania

Macierz podobieństwa

Narzędzia strony