Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat Knowledge Base » PQStat - Statistic » Plots » Kernel estimation
Pasek boczny
en:statpqpl:plotpl:kde1pl
Spis treści
Kernel estimation
One-dimensional kernel estimator
The one-dimensional kernel density estimator allows you to approximate the density of a data distribution by creating a smoothed density curve in a non-parametric way. It provides a better density estimate than is given by a traditional histogram, which columns form a staircase function.
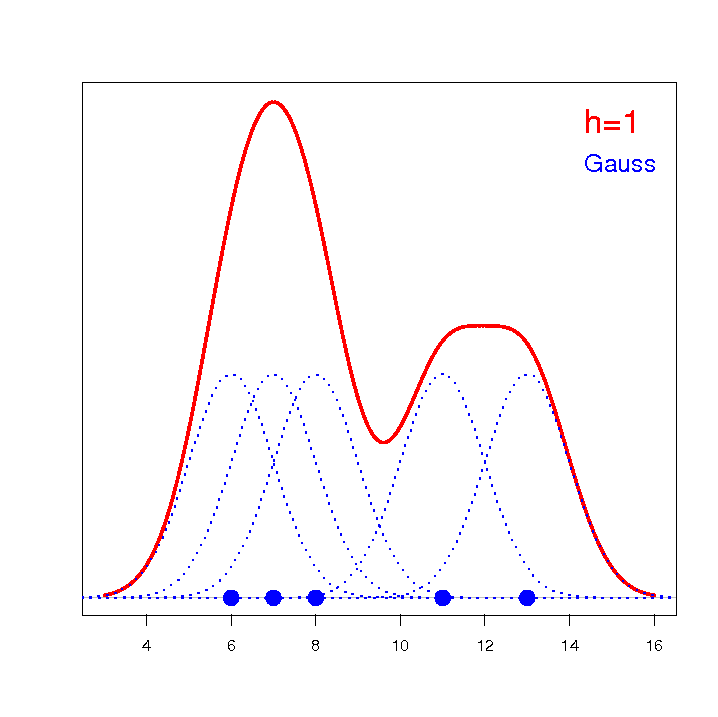
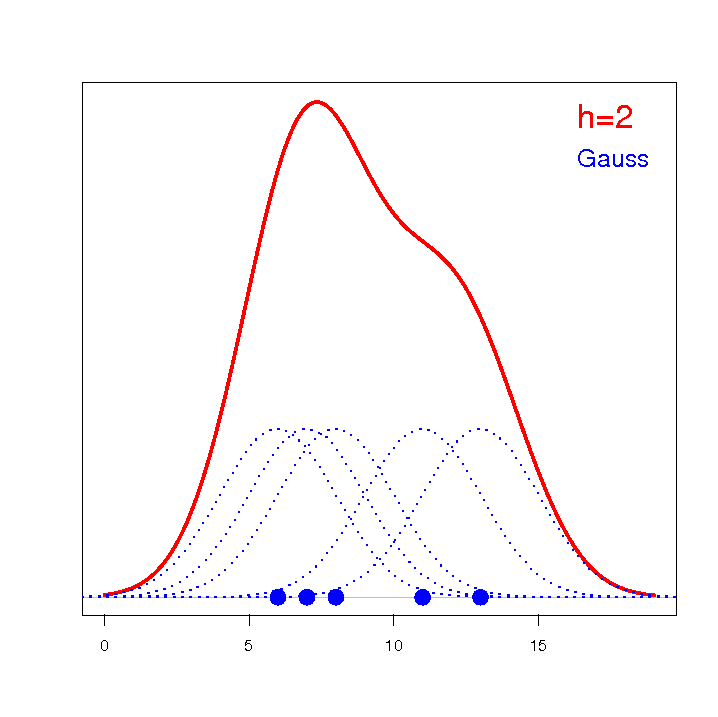
The kernel estimator is defined based on a properly smoothed kernel 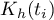 . The smoothing parameter
. The smoothing parameter 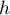 (bandwidth) has a decisive influence on the obtained estimator. The higher the value of the smoothing parameter, the greater the degree of smoothing.
(bandwidth) has a decisive influence on the obtained estimator. The higher the value of the smoothing parameter, the greater the degree of smoothing.
For each point 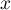 in the range defined by the data, the density is determined, that is, the value of the kernel estimator at that point is given. This estimator is created by summing the values of the kernel function
in the range defined by the data, the density is determined, that is, the value of the kernel estimator at that point is given. This estimator is created by summing the values of the kernel function 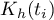 at that point:
at that point:
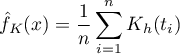
If we give the individual cases weights 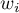 , then we can construct a weighted kernel density estimator defined by the formula:
, then we can construct a weighted kernel density estimator defined by the formula:
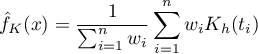
Smoothing factors
- User - gives you the ability to select any user-specified smoothing factor, but the factor must be positive.
- User scaled - is set so that the kernel function can be changed while remaining at the smoothing that was previously chosen for the Gauss kernel. In practice, by choosing a function other than Gauss, the smoothing factor is scaled (Scott, D. W. 19921)) so that the smoothing remains at a similar level as it was for the Gauss function. This offers the convenience of switching between different kernels without considering scaling the smoothing parameter. Scaling conversions are made based on the standard deviation:
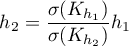
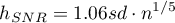
For a non-Gaussian kernel, the smoothing factor is subject to scaling (Scott D. W., 19924))
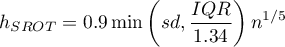
For a non-Gaussian kernel, the smoothing factor is subject to scaling (Scott D. W., 19927))
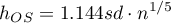
For a non-Gaussian kernel, the smoothing factor is subject to scaling (Scott D. W., 199210))
The kernel function affects the obtained value of the kernel estimator to a lesser extent than the smoothing parameter. The kernel is a probability density function built around each data point  . Typically, it is a symmetric function reaching a maximum at a point
. Typically, it is a symmetric function reaching a maximum at a point  , and decreasing its values as one moves away (increasing distance
, and decreasing its values as one moves away (increasing distance 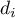 ) from that point. The distance from the analysed point is modified by the smoothing parameter
) from that point. The distance from the analysed point is modified by the smoothing parameter 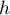 according to the formula:
according to the formula: 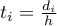 .
.
Depending on your needs, the kernel function can take the form of a function such as:
- Gauss
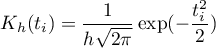
- uniform (rectanglular)
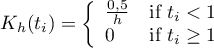
- triangular
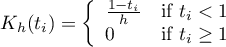
- Epanechnikov
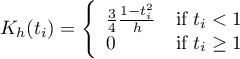
- quartic or biweight (fourth degree)
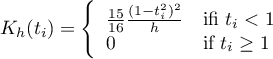
![LaTeX
\textcolor{green}{Gaussa}
\textcolor{red}{uniform}
\textcolor{blue}{triangular}
\textcolor{orange}{Epanechnikova}
\textcolor[rgb]{0,0.58,0}{quartic/biweight}](/lib/exe/fetch.php?media=wiki:latex:/img044e3e3cc3bfd6a6bd354c0e4f4e3f6c.png)
EXAMPLE (BMI.pqs file)
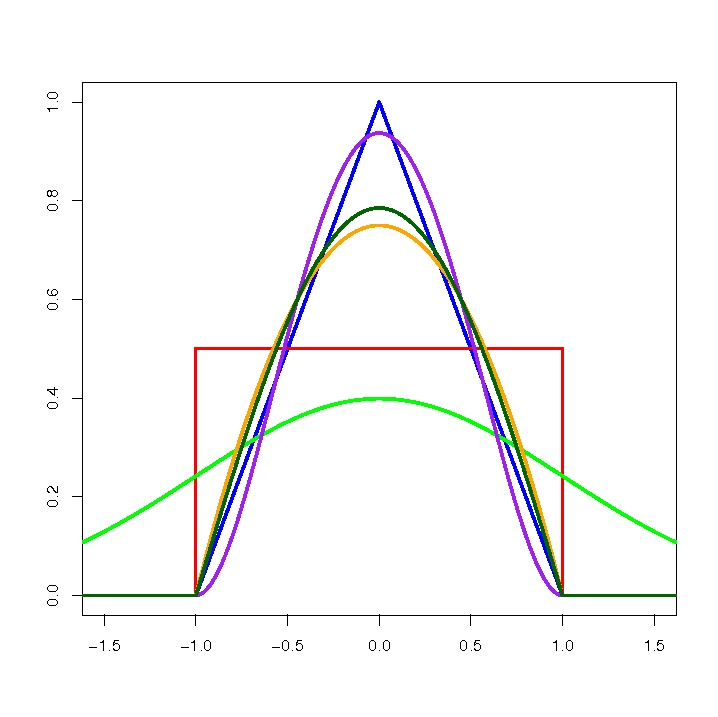
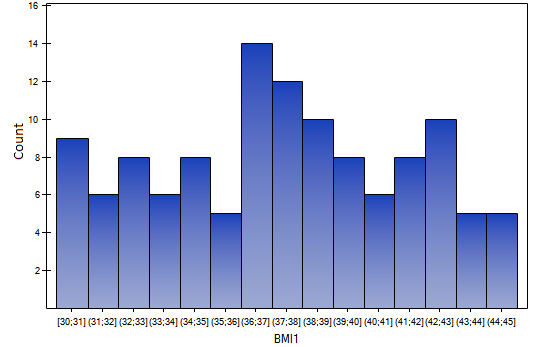
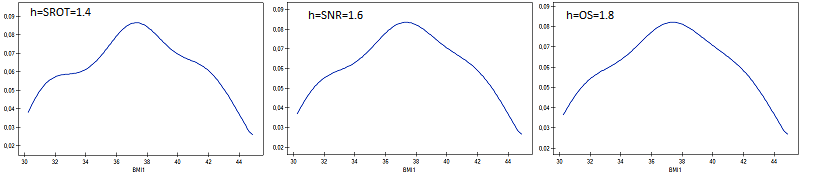
The values of the weight-growth index BMI1 for a certain group of obese subjects were calculated. Their distribution was presented using a histogram with the values divided every 1 BMI unit. The data were also visualized using a kernel density estimator by selecting a Gaussian kernel function and setting the smoothing factors to respectively: 0.5, 1, 2.
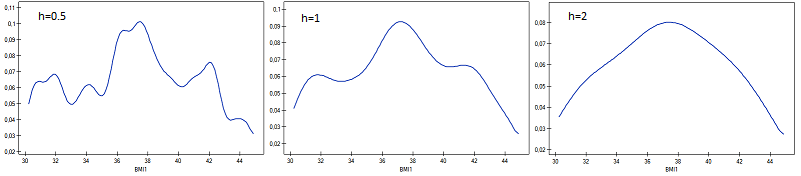
The smoothing factors of the kernel estimator suggested by the SROT, SNR, and OS methods reach magnitudes between 1.4 and 2.
1)
, 4)
, 7)
, 10)
Scott D. W., (1992), Multivariate Density Estimation. Theory, Practice and Visualization. New York: Wiley
2)
, 5)
Silverman B. W., (1986), Density estimation for statistics and data analysis, London: Chapman and Hall
3)
, 6)
Jones M. C., Marron J. S., Sheather S. J., (1996)., A brief survey of bandwidth selection for density estimation. J. Amer. Statist. Assoc. 91 401–407
8)
Terrell G.R., Scott D. W. (1985), Oversmoothed nonparametric density estimates. Journal of the American Statistical Association 80, 209-214
9)
Terrell G. R. (1990), The maximal smoothing principle in density estimation. Journal of the American Statistical Association 85, 470–477
en/statpqpl/plotpl/kde1pl.txt · ostatnio zmienione: 2022/02/11 18:00 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

