Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
pl:statpqpl:porown3grpl:parpl:anova_repeatedpl
ANOVA powtarzanych pomiarów
Jednoczynnikowa analiza wariancji dla powtarzanych pomiarów, czyli ANOVA dla grup zależnych (ang. single-factor repeated-measures analysis of variance) stosuje się w sytuacji, gdy pomiarów badanej zmiennej dokonujemy kilkukrotnie (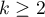 ) w różnych warunkach (przy czym zakładamy, że wariancje różnic pomiędzy wszystkimi parami pomiarów są sobie bliskie).
) w różnych warunkach (przy czym zakładamy, że wariancje różnic pomiędzy wszystkimi parami pomiarów są sobie bliskie).
Test ten służy do weryfikacji hipotezy o równości średnich badanej zmiennej w kilku (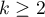 ) populacjach.
) populacjach.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- normalność rozkładu dla wszystkich zmiennych będących różnicą par pomiarowych (lub normalność badanej zmiennej dla każdego pomiaru),
Hipotezy:
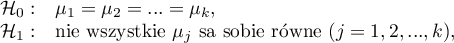
gdzie:
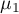 ,
,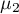 ,…,
,…,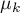 - średnie badanej zmiennej w kolejnych pomiarach z badanej populacji.
- średnie badanej zmiennej w kolejnych pomiarach z badanej populacji.
Statystyka testowa ma postać:
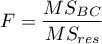
gdzie:
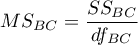 -średnia kwadratów między pomiarami,
-średnia kwadratów między pomiarami,
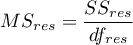 - średnia kwadratów dla reszt,
- średnia kwadratów dla reszt,
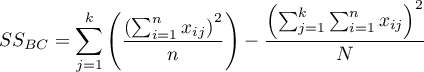 - suma kwadratów między pomiarami,
- suma kwadratów między pomiarami,
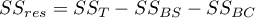 - suma kwadratów dla reszt,
- suma kwadratów dla reszt,
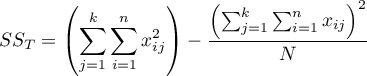 - całkowita suma kwadratów,
- całkowita suma kwadratów,
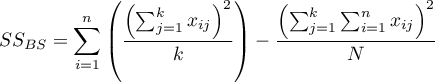 - suma kwadratów między obiektami,
- suma kwadratów między obiektami,
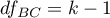 - stopnie swobody (między pomiarami),
- stopnie swobody (między pomiarami),
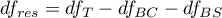 - stopnie swobody (dla reszt),
- stopnie swobody (dla reszt),
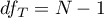 - całkowite stopnie swobody,
- całkowite stopnie swobody,
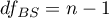 - stopnie swobody (między obiektami),
- stopnie swobody (między obiektami),
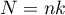 ,
,
 - liczność próby,
- liczność próby,
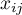 - wartości zmiennej dla
- wartości zmiennej dla  obiektów
obiektów 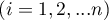 w
w  pomiarach
pomiarach  .
.
Statystyka ta podlega rozkładowi F Snedecora z 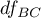 i
i 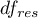 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Wielkość efektu - cząstkowa 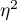
Wielkość ta określa proporcję wariancji wyjaśnionej do wariancji całkowitej związanej z danym czynnikiem. Zatem w modelu powtarzanych pomiarów wskazuje jaka część wewnątrzosobowej zmienności wyników może być przypisana powtarzanym pomiarom zmiennej.
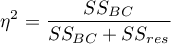
Testy POST-HOC
Wprowadzenie do kontrastów i testów POST-HOC przeprowadzone zostało w rozdziale dotyczącym jednoczynnikowej analizy wariancji.
Dla porównań prostych i złożonych (liczność w poszczególnych pomiarach zawsze jest taka sama).
Hipotezy:
Przykład - porównania proste (porównanie pomiędzy sobą 2 wybranych średnich):
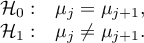
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
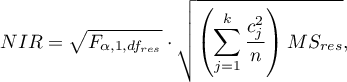
gdzie:
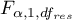 - to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności
- to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności  oraz dla stopni swobody odpowiednio: 1 i
oraz dla stopni swobody odpowiednio: 1 i 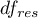 .
.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
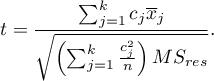
Statystyka ta podlega rozkładowi t-Studenta z 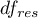 stopniami swobody.
stopniami swobody.
Uwaga!
Dla kontrastów wielkość 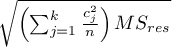 zastąpiona jest błędem kontrastu
zastąpiona jest błędem kontrastu 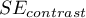 , a stopnie swobody to
, a stopnie swobody to 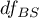 .
.
Dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:

gdzie:
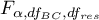 - to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności
- to wartość krytyczna (statystyka) rozkładu F Snedecora dla zadanego poziomu istotności  oraz
oraz 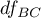 i
i 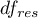 stopni swobody.
stopni swobody.
 Statystyka testowa ma postać:
Statystyka testowa ma postać:
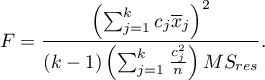
Statystyka ta podlega rozkładowi F Snedecora z 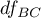 i
i 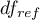 stopniami swobody.
stopniami swobody.
Dla porównań prostych (liczność w poszczególnych pomiarach zawsze jest taka sama).
 Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
Wartość najmniejszej istotnej różnicy wyliczana jest z wzoru:
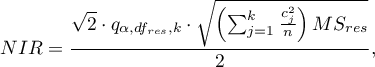
gdzie:
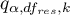 - to wartość krytyczna (statystyka) rozkładu studentyzowanego rozstępu dla zadanego poziomu istotności
- to wartość krytyczna (statystyka) rozkładu studentyzowanego rozstępu dla zadanego poziomu istotności  oraz
oraz 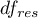 i
i  stopni swobody.
stopni swobody.
 ] Statystyka testowa ma postać:
] Statystyka testowa ma postać:
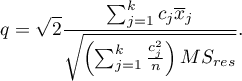
Statystyka ta podlega rozkładowi studentyzowanego rozstępu 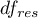 i
i  stopniami swobody.
stopniami swobody.
Info.
Algorytm obliczania wartości p i statystyki rozkładu studentyzowanego rozstępu w PQStat bazuje na pracy Lunda (1983)1). Inne programy lub strony internetowe mogą wyliczać nieco inne wartości niż PQStat, gdyż mogą bazować na mniej precyzyjnych lub bardziej restrykcyjnych algorytmach (Copenhaver i Holland (1988), Gleason (1999)).
Test dla trendu.
Test badający istnienie trendu może być wyliczany w takiej samej sytuacji jak ANOVA dla zmiennych zależnych, gdyż bazuje na tych samych założeniach, inaczej jednak ujmuje hipotezę alternatywną - wskazując w niej na istnienie trendu wartości średnich w kolejnych pomiarach. Analiza trendu w ułożeniu średnich oparta jest na kontrastach Test LSD Fishera. Budując odpowiednie kontrasty można badać dowolny rodzaj trendu np. liniowy, kwadratowy, sześcienny, itd. Tabela przykładowych wartości kontrastów dla wybranych trendów znajduje się w opisie testu dla trendu dla ANOVA zmiennych niezależnych.
Trend liniowy
Trend liniowy, tak jak pozostałe trendy, możemy analizować wpisując odpowiednie wartości kontrastów. Jeśli jednak znany jest kierunek trendu liniowego, wystarczy skorzystać z opcji Trend liniowy i wskazać oczekiwaną kolejność populacji przypisując im kolejne liczby naturalne.
Analiza przeprowadzana jest w oparciu o kontrast liniowy, czyli wskazanym według naturalnego uporządkowania grupom przypisane są odpowiednie wartości kontrastu i wyliczona zostaje statystyka Test LSD Fishera.
Przy znanym oczekiwanym kierunku trendu, hipoteza alternatywna jest jednostronna i interpretacji podlega jednostronna wartość  . Interpretacja dwustronnej wartości
. Interpretacja dwustronnej wartości  oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość
oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji jednoczynnikowej ANOVA dla grup zależnych wywołujemy poprzez menu Statystyka→Testy parametryczne→ANOVA dla grup zależnych lub poprzez Kreator.
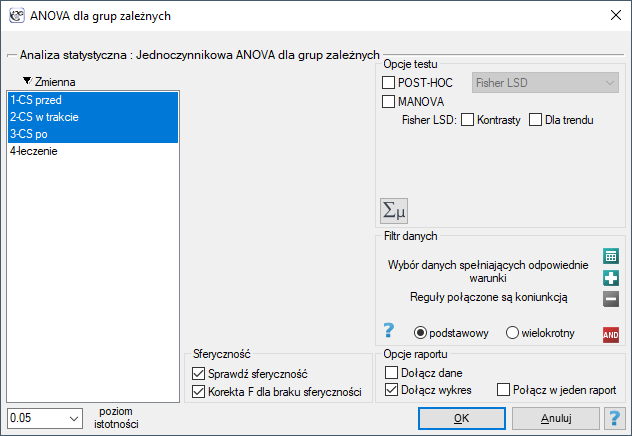
Patrz przykład (plik ciśnienie.pqs)
1)
Lund R.E., Lund J.R. (1983), Algorithm AS 190, Probabilities and Upper Quantiles for the Studentized Range. Applied Statistics; 34
pl/statpqpl/porown3grpl/parpl/anova_repeatedpl.txt · ostatnio zmienione: 2022/01/23 21:37 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


