Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Baza Wiedzy » statpqpl » Modele wielowymiarowe » Regresja logistyczna
Pasek boczny
pl:statpqpl:wielowympl:logistpl
Spis treści
Regresja logistyczna
Okno z ustawieniami opcji Regresji logistycznej wywołujemy poprzez menu Statystyka zaawansowana→Modele wielowymiarowe→Regresja logistyczna
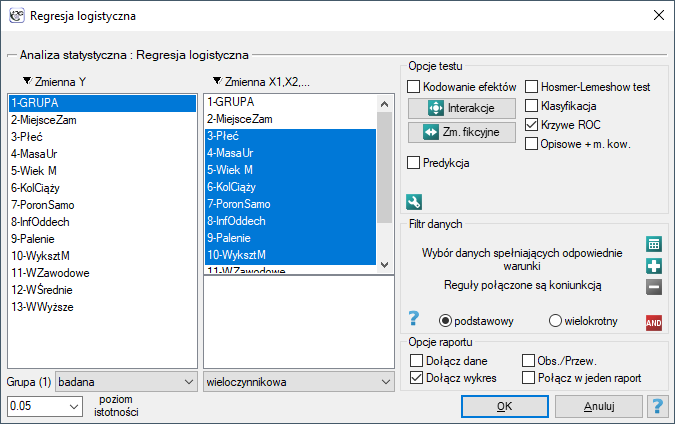

 Budowany model regresji logistycznej (podobnie jak liniowej regresji wielorakiej) pozwala na zbadanie wpływu wielu zmiennych niezależnych (
Budowany model regresji logistycznej (podobnie jak liniowej regresji wielorakiej) pozwala na zbadanie wpływu wielu zmiennych niezależnych (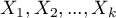 ) na jedną zmienną zależną (
) na jedną zmienną zależną ( ). Tym razem jednak zmienna zależna przyjmuje jedynie dwie wartości, np. chory/zdrowy, niewypłacalny/wypłacalny itp.
). Tym razem jednak zmienna zależna przyjmuje jedynie dwie wartości, np. chory/zdrowy, niewypłacalny/wypłacalny itp.
Owe dwie wartości kodowane są jako (1)/(0) gdzie:
(1) wartość wyróżniona - posiadanie danej cechy
(0) brak danej cechy.
Funkcja, na której oparty jest model regresji logistycznej wylicza nie dwupoziomową zmienną  , a prawdopodobieństwo przyjęcia przez tą zmienną wyróżnionej wartości:
, a prawdopodobieństwo przyjęcia przez tą zmienną wyróżnionej wartości:
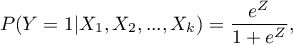 gdzie:
gdzie:
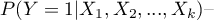 prawdopodobieństwo przyjęcia wartości wyróżnionej (1) pod warunkiem uzyskania konkretnych wartości zmiennych niezależnych, tzw. prawdopodobieństwo przewidywane dla 1.
prawdopodobieństwo przyjęcia wartości wyróżnionej (1) pod warunkiem uzyskania konkretnych wartości zmiennych niezależnych, tzw. prawdopodobieństwo przewidywane dla 1.
 najczęściej wyrażone jest zależnością liniową:
najczęściej wyrażone jest zależnością liniową:
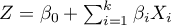 ,
,
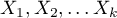 - zmienne niezależne, objaśniające,
- zmienne niezależne, objaśniające,
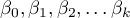 - parametry.
- parametry.
Zmienne fikcyjne i interakcje w modelu
Omówienie przygotowania zmiennych fikcyjnych i interakcji przedstawiono w rozdziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych.
Uwaga!
Funkcja Z może być również opisana zależnością wyższego stopnia np. kwadratową - do modelu wprowadzamy wówczas zmienną zawierającą kwadrat danej zmiennej niezależnej 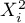 .
.
Logitem nazywamy przekształcenie tego modelu do postaci:
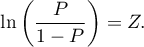
Macierze biorące udział w równaniu, dla próby o liczności  , zapisujemy następująco:
, zapisujemy następująco:
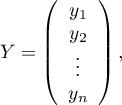

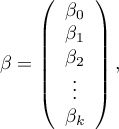
Rozwiązaniem równania jest wówczas wektor ocen parametrów 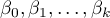 nazywanych współczynnikami regresji:
nazywanych współczynnikami regresji:
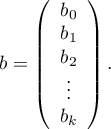
Współczynniki te szacowane są poprzez metodę największej wiarygodności czyli poprzez poszukiwanie maksimum funkcji wiarygodności 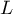 (w programie użyto algorytm iteracyjny Newton-Raphson) . Na podstawie tych wartości możemy wnioskować o wielkości wpływu zmiennej niezależnej (dla której ten współczynnik został oszacowany) na zmienną zależną.
(w programie użyto algorytm iteracyjny Newton-Raphson) . Na podstawie tych wartości możemy wnioskować o wielkości wpływu zmiennej niezależnej (dla której ten współczynnik został oszacowany) na zmienną zależną.
Każdy współczynnik obarczony jest pewnym błędem szacunku. Wielkość tego błędu wyliczana jest ze wzoru:
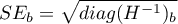 gdzie:
gdzie:
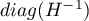 to główna przekątna macierzy kowariancji.
to główna przekątna macierzy kowariancji.
Uwaga!
Budując model należy pamiętać, że liczba obserwacji powinna być przynajmniej dziesięciokrotnie większa lub równa liczbie szacowanych parametrów modelu (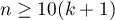 ). Jednak, coraz częściej stosuje się bardziej restrykcyjne kryterium zaproponowane przez P. Peduzzi i innych w roku 1996 1) mówiące, iż liczba obserwacji powinna być dziesięciokrotnie większa lub równa stosunkowi liczby zmiennych niezależnych (
). Jednak, coraz częściej stosuje się bardziej restrykcyjne kryterium zaproponowane przez P. Peduzzi i innych w roku 1996 1) mówiące, iż liczba obserwacji powinna być dziesięciokrotnie większa lub równa stosunkowi liczby zmiennych niezależnych (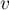 ) i mniejszej z proporcji liczności (
) i mniejszej z proporcji liczności ( ) opisanych z zmiennej zależnej (tzn. propoprcji chorych lub zdrowych), czyli (
) opisanych z zmiennej zależnej (tzn. propoprcji chorych lub zdrowych), czyli (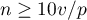 ).
).
Uwaga! Budując model należy pamiętać, że zmienne niezależne nie powinny być współliniowe. W przypadku gdy występuje współliniowość, estymacja może być niepewna a uzyskane wartości błędów bardzo wysokie. Zmienne współliniowe należy usunąć z modelu bądź zbudować z nich jedną zmienna niezależną np. zamiast współliniowych zmiennych: wiek matki i wiek ojca można zbudować zmienną wiek rodziców.
Uwaga! Kryterium zbieżności funkcji algorytmu iteracyjnego Newtona-Raphsona można kontrolować przy pomocy dwóch parametrów: limitu iteracji zbieżności (podaje maksymalną ilość iteracji w jakiej algorytm powinien osiągnąć zbieżność) i kryterium zbieżności (podaje wartość poniżej której uzyskana poprawa estymacji uznana będzie za nieznaczną i algorytm zakończy działanie).
Iloraz Szans
Jednostkowy Iloraz Szans
Na podstawie współczynników, dla każdej zmiennej niezależnej w modelu, wylicza się łatwą w interpretacji miarę jaką jest jednostkowy Iloraz Szans:
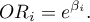
Otrzymany Iloraz Szans wyraża zmianę szansy na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna rośnie o 1 jednostkę. Wynik ten jest skorygowany o pozostałe zmienne niezależne znajdujące się w modelu w ten sposób, że zakłada iż pozostają one na stałym poziomie podczas, gdy badana zmienna niezależna rośnie o jednostkę.
Wartość OR interpretujemy następująco:
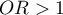 oznacza stymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile wzrasta szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.
oznacza stymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile wzrasta szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.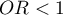 oznacza destymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile spada szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.
oznacza destymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile spada szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.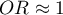 oznacza, że badana zmienna niezależna nie ma wpływu na uzyskanie wyróżnionej wartości (1).
oznacza, że badana zmienna niezależna nie ma wpływu na uzyskanie wyróżnionej wartości (1).
[Iloraz Szans - wzór ogólny]
Program PQStat wylicza jednostkowy Iloraz Szans. Jego modyfikacja, na podstawie ogólnego wzoru, umożliwia zmianę interpretacji uzyskanego wyniku.
Iloraz szans na wystąpienie stanu wyróżnionego w ogólnym przypadku jest wyliczany jako iloraz dwóch szans. Zatem dla zmiennej niezależnej  dla
dla  wyrażonego zależnością liniową wyliczamy:
wyrażonego zależnością liniową wyliczamy:
szansę dla kategorii pierwszej:
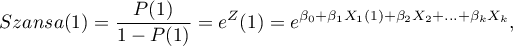
szansę dla kategorii drugiej:
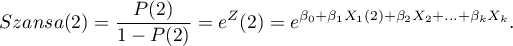
Iloraz Szans dla zmiennej  wyraża się wówczas wzorem:
wyraża się wówczas wzorem:
![LaTeX \begin{displaymath}
\begin{array}{lll}
OR_1(2)/(1) &=&\frac{Szansa(2)}{Szansa(1)}=\frac{e^{\beta_0+\beta_1X_1(2)+\beta_2X_2+...+\beta_kX_k}}{e^{\beta_0+\beta_1X_1(1)+\beta_2X_2+...+\beta_kX_k}}\\
&=& e^{\beta_0+\beta_1X_1(2)+\beta_2X_2+...+\beta_kX_k-[\beta_0+\beta_1X_1(1)+\beta_2X_2+...+\beta_kX_k]}\\
&=& e^{\beta_1X_1(2)-\beta_1X_1(1)}=e^{\beta_1[X_1(2)-X_1(1)]}=\\
&=& \left(e^{\beta_1}\right)^{[X_1(2)-X_1(1)]}.
\end{array}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img5e7d555cf6560897adceb6c87ea41a56.png)
Przykład
Jeśli zmienną niezależną jest wiek wyrażony w latach, to różnica pomiędzy sąsiadującymi kategoriami wieku np. 25 lat i 26 lat wynosi 1 rok 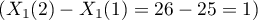 . Wówczas otrzymamy jednostkowy Iloraz Szans:
. Wówczas otrzymamy jednostkowy Iloraz Szans:
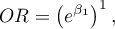 który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 1 rok.
który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 1 rok.
Iloraz szans wyliczony dla niesąsiadujących kategorii zmiennej wiek np. 25 lat i 30 lat będzie pięcioletnim Ilorazem Szans, ponieważ różnica 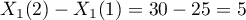 . Wówczas otrzymamy pięcioletni Iloraz Szans:
. Wówczas otrzymamy pięcioletni Iloraz Szans:
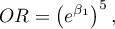 który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 5 lat.
który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 5 lat.
Uwaga!
Jeśli analizę przeprowadzamy dla modelu innego niż liniowy, lub uwzględniamy interakcję, wówczas na podstawie ogólnego wzoru możemy wyliczyć odpowiedni Ilorazu Szans zmieniając formułę wyrażającą  .
.
Przykład c.d. (plik zadanie.pqs)
Przykład c.d. (wada.pqs)
2014/08/22 20:00
Weryfikacja modelu
Istotność statystyczna poszczególnych zmiennych w modelu (istotność ilorazu szans)
Na podstawie współczynnika oraz jego błędu szacunku możemy wnioskować czy zmienna niezależna, dla której ten współczynnik został oszacowany wywiera istotny wpływ na zmienną zależną. W tym celu posługujemy się testem Walda.
Hipotezy:
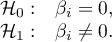 lub równoważnie:
lub równoważnie:
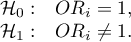
Statystykę testową testu Walda wyliczamy według wzoru:
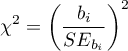 Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z  stopniem swobody .
stopniem swobody .
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Jakość zbudowanego modelu
Dobry model powinien spełniać dwa podstawowe warunki: powinien być dobrze dopasowany i możliwie jak najprostszy. Jakość modelu regresji logistycznej możemy ocenić kilkoma miarami, które opierają się na:
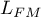 - maksimum funkcji wiarygodności modelu pełnego (z wszystkimi zmiennymi),
- maksimum funkcji wiarygodności modelu pełnego (z wszystkimi zmiennymi),
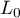 - maksimum funkcji wiarygodności modelu zawierającego jedynie wyraz wolny,
- maksimum funkcji wiarygodności modelu zawierającego jedynie wyraz wolny,
 - liczności próby.
- liczności próby.
- Kryteria informacyjne opierają się na entropii informacji niesionej przez model (niepewności modelu) tzn. szacują utraconą informację, gdy dany model jest używany do opisu badanego zjawiska. Powinniśmy zatem wybierać model o minimalnej wartości danego kryterium informacyjnego.
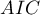 ,
, 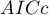 i
i 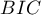 jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby zmiennych w modelu (
jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby zmiennych w modelu ( ) i liczności próby (
) i liczności próby ( ). W obu przypadkach element ten rośnie wraz ze wzrostem liczby zmiennych i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
). W obu przypadkach element ten rośnie wraz ze wzrostem liczby zmiennych i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
Kryterium informacyjne nie jest jednak miarą absolutną, tzn. jeśli wszystkie porównywane modele źle opisują rzeczywistość w kryterium informacyjnym nie ma sensu szukać ostrzeżenia.
- Kryterium informacyjne Akaikego (ang. Akaike information criterion)
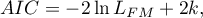
Jest to kryterium asymptotyczne - odpowiednie dla dużych prób.
- Poprawione kryterium informacyjne Akaikego
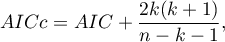
Poprawka kryterium Akaikego dotyczy wielkości próby, przez co jest to miara rekomendowana również dla prób o małych licznościach.
- Bayesowskie kryterium informacyjne Schwartza (ang. Bayes Information Criterion lub Schwarz criterion)
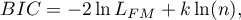
Podobnie jak poprawione kryterium Akaikego uwzględnia wielkość próby.
- Pseudo R
 - tzw. McFadden R
- tzw. McFadden R jest miarą dopasowania modelu (odpowiednikiem współczynnika determinacji wielorakiej
jest miarą dopasowania modelu (odpowiednikiem współczynnika determinacji wielorakiej  wyznaczanego dla liniowej regresji wielorakiej) .
wyznaczanego dla liniowej regresji wielorakiej) .
Wartość tego współczynnika mieści się w przedziale 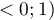 , gdzie wartości bliskie 1 oznaczają doskonałe dopasowanie modelu,
, gdzie wartości bliskie 1 oznaczają doskonałe dopasowanie modelu, 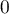 - zupełny bark dopasowania. Współczynnik
- zupełny bark dopasowania. Współczynnik 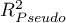 wyliczamy z wzoru:
wyliczamy z wzoru:
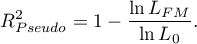
Ponieważ współczynnik 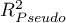 nie przyjmuje wartości 1 i jest wrażliwy na ilość zmiennych w modelu, wyznacza się jego poprawioną wartość:
nie przyjmuje wartości 1 i jest wrażliwy na ilość zmiennych w modelu, wyznacza się jego poprawioną wartość:
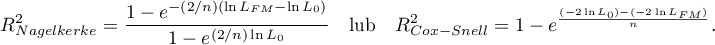
- Istotność statystyczna wszystkich zmiennych w modelu
Podstawowym narzędziem szacującym istotność wszystkich zmiennych w modelu jest test ilorazu wiarygodności. Test ten weryfikuje hipotezę:
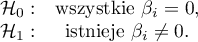
Statystyka testowa ma postać:
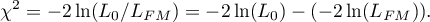
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z  stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

- Test Hosmera-Lemeshowa - Test ten, dla różnych podgrup danych, porównuje obserwowane liczności występowania wartości wyróżnionej
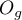 i przewidywane prawdopodobieństwo
i przewidywane prawdopodobieństwo 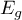 . Jeśli
. Jeśli 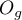 i
i 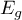 są wystarczająco bliskie, wówczas można założyć, że zbudowano dobrze dopasowany model.
są wystarczająco bliskie, wówczas można założyć, że zbudowano dobrze dopasowany model.
Do obliczeń najpierw obserwacje są dzielone na 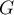 podgrup - zwykle na decyle (
podgrup - zwykle na decyle (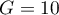 ).
).
Hipotezy:
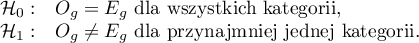
Statystyka testowa ma postać:
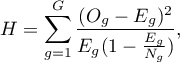 gdzie:
gdzie:
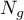 - liczba obserwacji w grupie
- liczba obserwacji w grupie 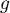 .
.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 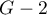 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

 AUC - pole pod krzywą ROC - Krzywa ROC, zbudowana w oparciu o wartość zmiennej zależnej oraz przewidywane prawdopodobieństwo zmiennej zależnej
AUC - pole pod krzywą ROC - Krzywa ROC, zbudowana w oparciu o wartość zmiennej zależnej oraz przewidywane prawdopodobieństwo zmiennej zależnej 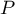 , pozwala na ocenę zdolności zbudowanego modelu regresji logistycznej do klasyfikacji przypadków do dwóch grup: (1) i (0). Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną modelu. Gdy krzywa ROC pokrywa się z przekątną
, pozwala na ocenę zdolności zbudowanego modelu regresji logistycznej do klasyfikacji przypadków do dwóch grup: (1) i (0). Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną modelu. Gdy krzywa ROC pokrywa się z przekątną  , to decyzja o przyporządkowaniu przypadku do wybranej klasy (1) lub (0) podejmowana na podstawie modelu jest tak samo dobra jak losowy podział badanych przypadków do tych grup. Jakość klasyfikacyjna modelu jest dobra, gdy krzywa znajduje się znacznie powyżej przekątnej
, to decyzja o przyporządkowaniu przypadku do wybranej klasy (1) lub (0) podejmowana na podstawie modelu jest tak samo dobra jak losowy podział badanych przypadków do tych grup. Jakość klasyfikacyjna modelu jest dobra, gdy krzywa znajduje się znacznie powyżej przekątnej  , czyli gdy pole pod krzywą ROC jest znacznie większe niż pole pod prostą
, czyli gdy pole pod krzywą ROC jest znacznie większe niż pole pod prostą  , zatem większe niż
, zatem większe niż 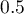
Hipotezy:
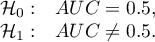
Statystyka testowa ma postać:
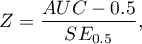 gdzie:
gdzie:
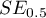 - błąd pola.
- błąd pola.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Dodatkowo, dla krzywej ROC podawana jest proponowana wartość punktu odcięcia prawdopodobieństwa przewidywanego, oraz tabela podająca wielkość czułości i swoistości dla każdego możliwego punktu odcięcia.
Uwaga! Więcej możliwości w wyliczeniu punktu odcięcia daje moduł **Krzywa ROC**. Analizę przeprowadzamy na podstawie wartości obserwowanych i prawdopodobieństwa przewidywanego, które uzyskujemy w analizie regresji logistycznej.
- Klasyfikacja
Na podstawie wybranego punktu odcięcia prawdopodobieństwa przewidywanego można sprawdzić jakość klasyfikacji. Punkt odcięcia, to domyślnie wartość 0.5. Użytkownik może zmienić tę wartość na dowolną wartość z przedziału  np. wartość sugerowaną przez krzywą ROC.
np. wartość sugerowaną przez krzywą ROC.
W wyniku uzyskamy tabelę klasyfikacji oraz procent poprawnie zaklasyfikowanych przypadków, procent poprawnie zaklasyfikowanych (0) - swoistość oraz procent poprawnie zaklasyfikowanych (1) - czułość.
2014/08/22 20:00
Wykresy w regresji logistycznej
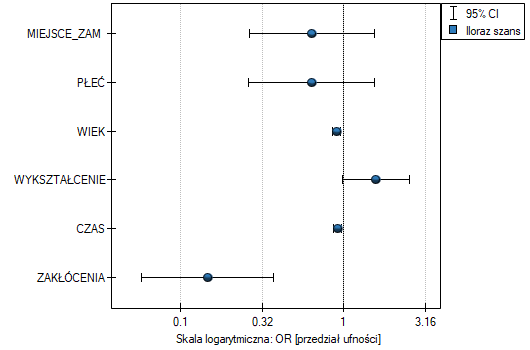
- Iloraz szans i przedział ufności - to wykres przedstawiający OR wraz z 95% przedziałem ufności dla wyniku każdej zmiennej zwróconej w zbudowanym modelu. Dla zmiennych kategorialnych, linia na poziomie 1 wskazuje wartość ilorazu szans dla kategorii referencyjnej.
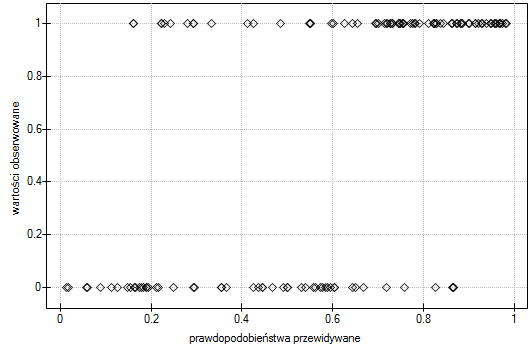
- Wartości obserwowane / Prawdopodobieństwo oczekiwane - to wykres przedstawiający wyniki przewidywanego dla każdej osoby prawdopodobieństwa wystąpienia zdarzenia (oś X) oraz wartości prawdziwej, czyli wystąpienia zdarzenia (wartość 1 na osi Y) lub braku zdarzenia (wartość 0 na osi Y). Jeśli model bardzo dobrze prognozuje, to przy lewej stronie wykresu punkty będą się kumulowały w dolnej części, a przy prawej stronie wykresu w górnej części.
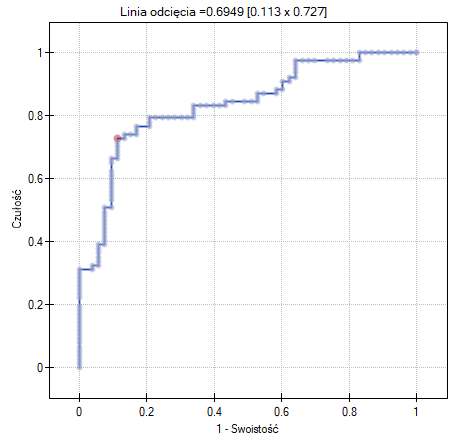
- Krzywa ROC - to wykres zbudowany w oparciu o wartość zmiennej zależnej oraz przewidywane prawdopodobieństwo wystąpienia zdarzenia.
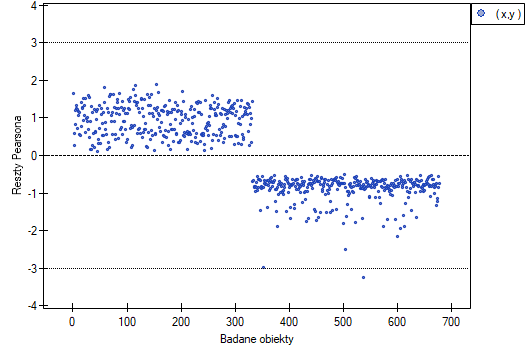
- Wykres reszt Pearsona - to wykres pozwalający ocenić czy występują odstające dane. Reszty to różnice wartości obserwowanej i przewidywanego przez model prawdopodobieństwa. Wykresy surowych reszt z regresji logistycznej trudno interpretować, dlatego ujednolica się je wyznaczając reszty Pearsona. Reszta Pearsona to surowa reszta podzielona przez pierwiastek kwadratowy z funkcji wariancji. Znak (dodatni lub ujemny) wskazuje, czy obserwowana wartość jest wyższa, czy niższa niż wartość dopasowana do modelu, a wielkość wskazuje stopień odchylenia. Reszty Persona mniejsze lub większe niż 3 sugerują, zbyt duże odchylenie danego obiektu.
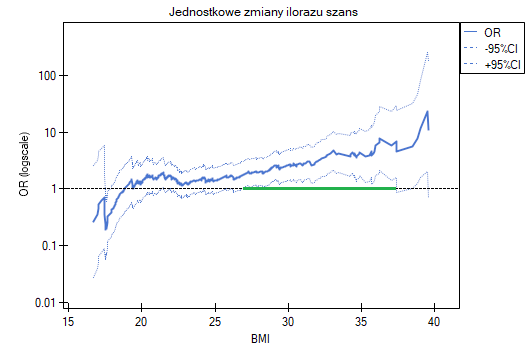
- Jednostkowe zmiany ilorazu szans - to wykres przedstawiający serie ilorazów szans wraz z przedziałem ufności, wyznaczane dla każdego z możliwych punktów odcięcia zmiennej umieszczonej na osi X. Umożliwia on użytkownikowi wybór jednego, dobrego punktu odcięcia i następnie zbudowania na tej podstawie nowej dwuwartościowej zmiennej, przy której zostanie osiągnięty odpowiednio wysoki lub niski iloraz szans. Wykres dedykowany jest dla oceny zmiennych ciągłych w analizie jednoczynnikowej, tzn. gdy wybrana jest tylko jedna zmienna niezależna.
- Profile ilorazu szans - to wykres przedstawiający serie ilorazów szans wraz z przedziałem ufności, wyznaczane dla wskazanej wielkości okna tzn. porównujące częstości wewnątrz okna z częstościami umieszczonymi na zewnątrz okna. Umożliwia to użytkownikowi wybór kilku kategorii na jakie chce podzielić badaną zmienną i przyjęcie najkorzystniejszej kategorii referencyjnej. Najlepiej sprawdza się, gdy poszukujemy funkcji U-kształtnej tzn. o wysokim ryzyku przy niskich i przy wysokich wartościach badanej zmiennej, a o niskim przy wartościach przeciętnych. Nie ma jednej dobrej dla każdej analizy wielkości okna, wielkość tę należy ustalać indywidualnie dla każdej zmiennej. Wielkość okna wskazuje liczbę niepowtarzalnych wartości zmiennej X znajdujących się w oknie. Im szersze okno, tym większe uogólnienie wyników i gładsza funkcja ilorazu szans. Im węższe okno, tym bardziej szczegółowe wyniki, przez co bardziej rozchwiany iloraz szans. Do wykresu dodana jest krzywa ukazująca wygładzoną (metodą Lowess) wartość ilorazu szans. Ustawiając bliski 0 współczynnik wygładzania uzyskamy krzywą przylegającą ściśle do wyznaczonego ilorazu szans, natomiast ustawiając współczynnik wygładzania bliżej 1 dostaniemy większe uogólnienie ilorazu szans, a więc bardziej gładką i mniej przyległą do ilorazu szans krzywą. Wykres dedykowany jest dla oceny zmiennych ciągłych w analizie jednoczynnikowej, tzn. gdy wybrana jest tylko jedna zmienna niezależna.
Przykład (plik Profile OR.pqs)
Badamy ryzyko występowania choroby A i choroby B w zależności od BMI pacjenta. Ponieważ BMI jest zmienną ciągłą, to jej umieszczenie w modelu skutkuje wyznaczeniem jednostkowego ilorazu szans wyznaczającego liniowy trend wzrostu lub spadku ryzyka. Nie wiemy czy model liniowy będzie dobrym modelem dla analizy tego ryzyka, dlatego przed budowaniem wielowymiarowych modeli regresji logistycznej zbudujemy kilka modeli jednowymiarowych prezentujących tę zmienną na wykresach, by móc ocenić kształt badanej zależności i na tej podstawie zdecydować o sposobie w jaki powinniśmy przygotować zmienną do analizy. Do tego celu posłużą wykresy jednostkowych zmiany ilorazu szans i profili ilorazu szans, przy czym dla profili wybierzemy okno o wielkości 100, ponieważ prawie każdy pacjent ma inne BMI, więc około 100 pacjentów znajdzie się w każdym oknie.
- Choroba A
Jednostkowe zmiany ilorazu szans pokazują, że gdy punkt odcięcia BMI wybierzemy gdzieś między 27 a 37, to uzyskamy istotny statystycznie i dodatni iloraz szans pokazujący, że osoby mające BMI powyżej tej wartości mają istotnie wyższe ryzyko choroby niż osoby poniżej tej wartości.
Profile ilorazu szans pokazują, że czerwona krzywa znajduje się wciąż blisko jedynki, nieco wyżej jest tylko końcówka krzywej, co wskazuje że może być trudno podzielić BMI na więcej niż 2 kategorie i wybrać dobrą kategorię referencyjną, tzn. taką, która da istotne ilorazy szans.
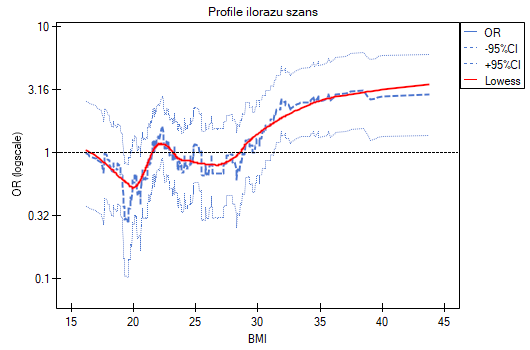
Podsumowując, można skorzystać z podziału BMI na dwie wartości (np. odnieść osoby z BMI powyżej 30 do tych z BMI poniżej tej granicy, wówczas OR[95%CI]=[1.41, 4.90], p=0.0024) lub pozostać przy jednostkowym ilorazie szans, wskazującym stały wzrost ryzyka choroby przy wzroście BMI o jednostkę (OR[95%CI]=1.07[1.02, 1.13], p=0.0052).
- Choroba B
Jednostkowe zmiany ilorazu szans pokazują, że gdy punkt odcięcia BMI wybierzemy gdzieś między 22 a 35, to uzyskamy istotny statystycznie i dodatni iloraz szans pokazujący, że osoby mające BMI powyżej tej wartości mają istotnie wyższe ryzyko choroby niż osoby poniżej tej wartości.
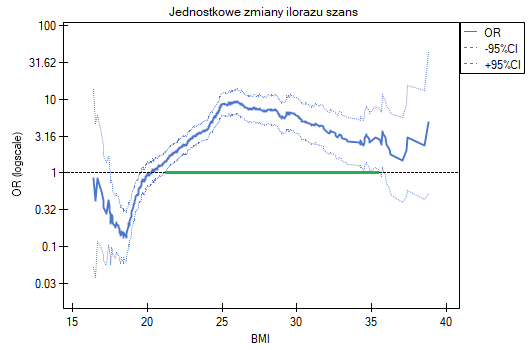
Profile ilorazu szans pokazują, że znacznie lepiej byłoby podzielić BMI na 2 lub 4 kategorie. Przy czym kategorią referencyjną powinna być kategoria obejmująca BMI gdzieś pomiędzy 19 a 25, ponieważ to ta kategoria znajduje się najniżej i jest mocno oddalona od wyników dla BMI znajdujących się na lewo i na prawo od tego przedziału. Widzimy wyraźny kształt przypominający literę U, co oznacza, że ryzyko choroby jest wysokie przy niskim i przy wysokim BMI.
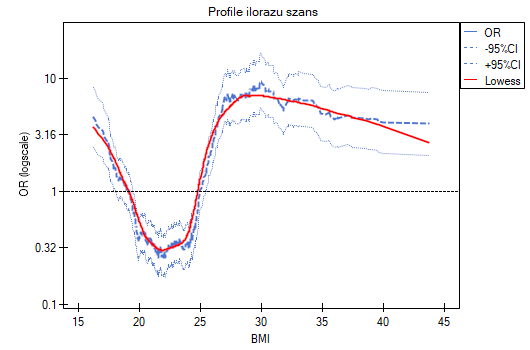
Podsumowując, mimo, że zależność dla jednostkowego ilorazu szans, czyli zależność liniowa jest istotna statystycznie, to nie warto budować takiego właśnie modelu. Znacznie lepiej podzielić BMI na kategorie. Podział pokazujący najlepiej kształt tej zależności, to podział wykorzystujący dwie lub trzy kategorie BMI, gdzie wartością odniesienia będzie przeciętne BMI. Wykorzystując standardowy podział BMI i ustanawiając kategorią odniesienia BMI w normie uzyskamy ponad 15 krotnie wyższe ryzyko dla osób z niedowagą (OR[95%CI]=15.14[6.93, 33.10]), ponad dziesięciokrotnie dla osób z nadwagą (OR[95%CI]=10.35[6.74, 15.90]) i ponad dwunastokrotnie dla osób z otyłością (OR[95%CI]=12.22[6.94, 21.49]).
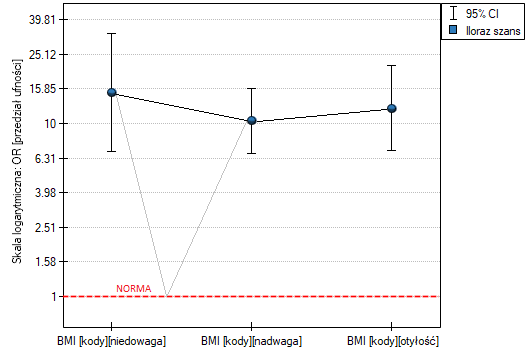
Na wykresie ilorazów szans norma BMI wskazana jest na poziomie 1, jako kategoria referencyjna. Dorysowaliśmy linie łączące uzyskane OR i również normę, tak by pokazać, że uzyskany kształt zależności jest tożsamy z wyznaczonym wcześniej poprzez profil ilorazu szans.
2021/01/11 22:02
Przykłady dla regresji logistycznej
Przeprowadzono badanie mające na celu identyfikację czynników ryzyka pewnej rzadko występującej wady wrodzonej u dzieci. W badaniu wzięło udział 395 matek dzieci z ta wadą oraz 375 matek dzieci zdrowych. Zebrane dane to: miejsce zamieszkania, płeć dziecka, masa urodzeniowa dziecka, wiek matki, kolejność ciąży, przebyte poronienia samoistne, infekcje oddechowe, palenie tytoniu, wykształcenie matki.
Budujemy model regresji logistycznej by sprawdzić które zmienne mogą wywierać istotny wpływ na występowanie wady. Jako zmienną zależną ustawiamy kolumnę GRUPA, wartością wyróżnioną w tej zmiennej jako  jest grupa
jest grupa badana, czyli matki dzieci z wadą wrodzoną. Kolejne 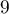 zmiennych, to zmienne niezależne:
zmiennych, to zmienne niezależne:
MiejsceZam (2=miasto/1=wieś),
Płeć (1=mężczyzna/0=kobieta),
MasaUr (w kilogramach z dokładnością do 0.5kg),
WiekM (w latach),
KolCiąży (dziecko z której ciąży),
PoronSamo (1=tak/0=nie),
InfOddech (1=tak/0=nie),
Palenie (1=tak/0=nie),
WyksztM (1=podstawowe lub niżej/2=zawodowe/3=średnie/4=wyższe).
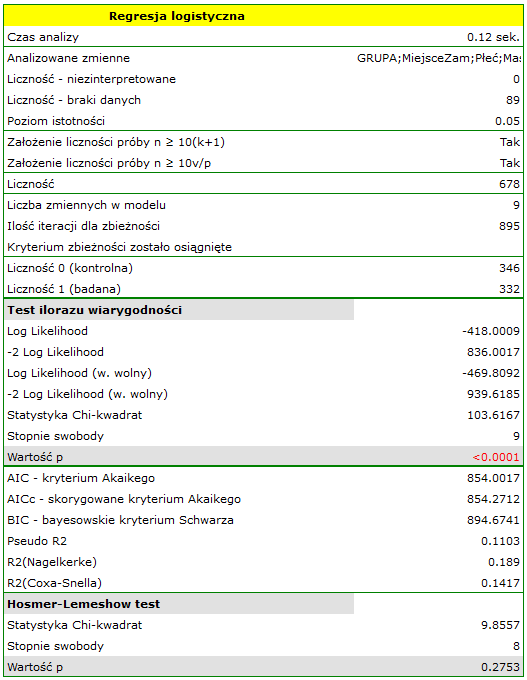
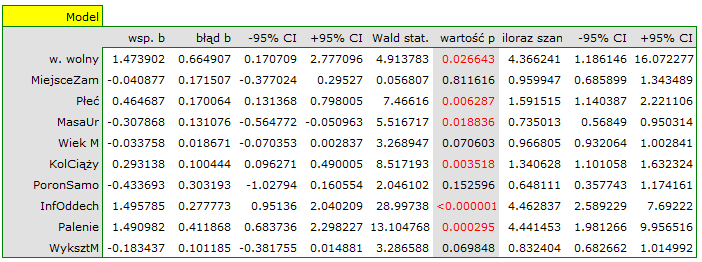
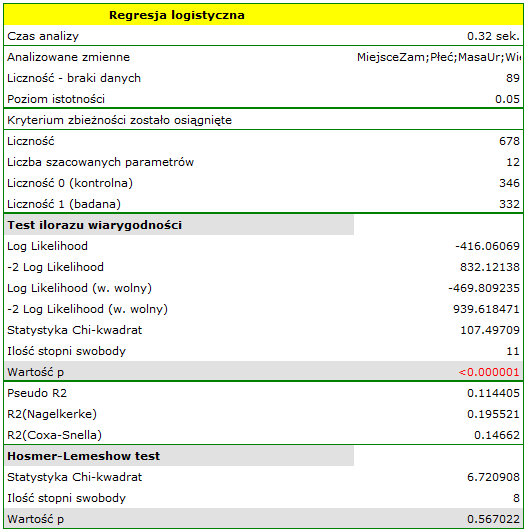
Jakość dopasowania modelu nie jest wysoka (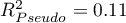 ,
, 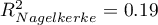 i
i 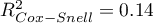 ). Jednocześnie model jest istotny statystycznie (wartość
). Jednocześnie model jest istotny statystycznie (wartość 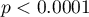 testu ilorazu wiarygodności), a zatem część zmiennych niezależnych znajdujących się w modelu jest istotna statystycznie. Wynik testu Hosmera-Lemeshowa wskazuje na brak istotności (
testu ilorazu wiarygodności), a zatem część zmiennych niezależnych znajdujących się w modelu jest istotna statystycznie. Wynik testu Hosmera-Lemeshowa wskazuje na brak istotności (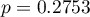 ). Przy czym, w przypadku testu Hosmera-Lemeshowa pamiętamy o tym, że brak istotności jest pożądany, bo wskazuje na podobieństwo liczności obserwowanych i prawdopodobieństwa przewidywanego.
). Przy czym, w przypadku testu Hosmera-Lemeshowa pamiętamy o tym, że brak istotności jest pożądany, bo wskazuje na podobieństwo liczności obserwowanych i prawdopodobieństwa przewidywanego.
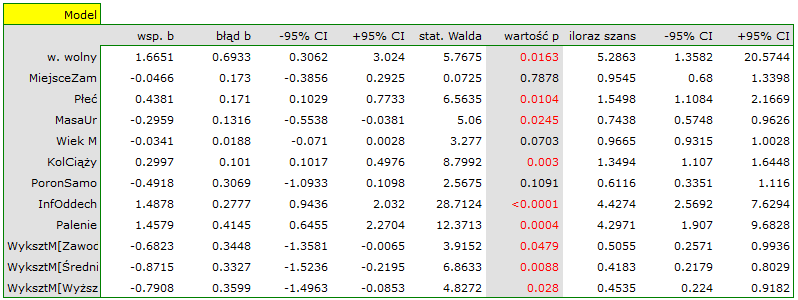
Interpretacja poszczególnych zmiennych w modelu zaczyna się od sprawdzenia ich istotności. W tym przypadku zmienne, które w istotny sposób są związane z występowaniem wady to:
Płeć: 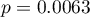 ,
,
MasaUr: 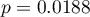 ,
,
KolCiąży: 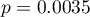 ,
,
InfOddech: 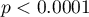 ,
,
Palenie: 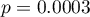 .
.
Badana wada wrodzona jest wadą rzadką, ale szansa na jej wystąpienie zależy od wymienionych zmiennych w sposób opisany poprzez iloraz szans:
- zmienna Płeć:
![LaTeX $OR[95\%CI]=1.60[1.14;2.22]$](/lib/exe/fetch.php?media=wiki:latex:/imgf8dc809d4d33fbf457e222bb2a246674.png) - szansa wystąpienia wady u chłopca jest
- szansa wystąpienia wady u chłopca jest 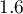 krotnie większa niż u dziewczynki;
krotnie większa niż u dziewczynki;
- zmienna MasaUr:
![LaTeX $OR[95\%CI]=0.74[0.57;0.95]$](/lib/exe/fetch.php?media=wiki:latex:/img5e023481fc641b1a88b75e8a1b4ba8be.png) - im wyższa masa urodzeniowa, tym szansa wystąpienia wady u dziecka jest mniejsza;
- im wyższa masa urodzeniowa, tym szansa wystąpienia wady u dziecka jest mniejsza;
- zmienna KolCiąży:
![LaTeX $OR[95\%CI]=1.34[1.10;1.63]$](/lib/exe/fetch.php?media=wiki:latex:/imgbc4c66db7606d854bbbbe9db1cbb0a16.png) - szansa wystąpienia wady u dziecka wzrasta wraz z każdą kolejną ciążą
- szansa wystąpienia wady u dziecka wzrasta wraz z każdą kolejną ciążą 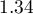 krotnie;
krotnie;
- zmienna InfOddech:
![LaTeX $OR[95\%CI]=4.46[2.59;7.69]$](/lib/exe/fetch.php?media=wiki:latex:/imga1c2b1a351fce6107ff7c7ccc044c83d.png) - szansa wystąpienia wady u dziecka, gdy matka w czasie ciąży przechodziła infekcje oddechową jest
- szansa wystąpienia wady u dziecka, gdy matka w czasie ciąży przechodziła infekcje oddechową jest 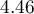 krotnie większa niż gdyby jej nie przechodziła;
krotnie większa niż gdyby jej nie przechodziła;
- zmienna Palenie:
![LaTeX $OR[95\%CI]=4.44[1.98;9.96]$](/lib/exe/fetch.php?media=wiki:latex:/img14fd8b0c97c85092641099b3a0c857d8.png) - matka paląca w czasie ciąży zwiększa
- matka paląca w czasie ciąży zwiększa 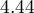 krotnie szansę na wystąpienia wady u dziecka
krotnie szansę na wystąpienia wady u dziecka
W przypadku zmiennych nieistotnych statystycznie przedział ufności dla Ilorazu Szans zawiera jedynkę co oznacza, że zmienne te nie zwiększają ani nie zmniejszają szansy na wystąpienie badanej wady. Nie można więc interpretować uzyskanego ilorazu w podobny sposób jak dla zmiennych istotnych statystycznie.
Wpływ poszczególnych zmiennych niezależnych na występowanie wady możemy równiez opisać przy pomocy wykresu dotyczącego ilorazu szans:
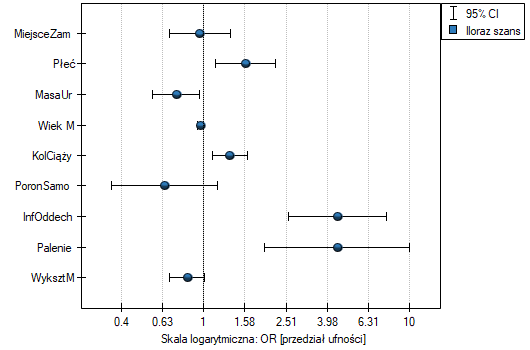
Przykład c.d. (wada.pqs)
Zbudujemy raz jeszcze model regresji logistycznej, ale tym razem zmienną wykształcenie rozbijemy na zmienne fikcyjne (kodowanie zero-jedynkowe). Tracimy tym samym informację o uporządkowaniu kategorii wykształcenia, ale zyskujemy możliwość wnikliwszej analizy poszczególnych kategorii. Rozbicia na zmienne fikcyjne dokonujemy wybierając w oknie analizy Zm. fikcyjne:
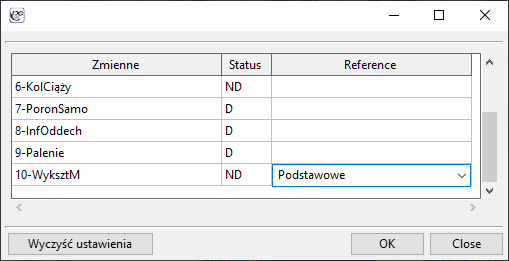
Wykształcenie podstawowe wybieramy jako kategorię odniesienia.
W rezultacie zmienne opisujące wykształcenie stają się istotne statystycznie. Dopasowanie modelu nie ulega znacznej zmianie, ale zmienia się sposób interpretacji ilorazu szans dla wykształcenia:
![LaTeX \begin{tabular}{|l|l|}
\hline
\textbf{Zmienna}& $OR[95\%CI]$ \\\hline
Wykształcenie podstawowe& kategoria referencyjna\\
Wykształcenie zawodowe& $0.51[0.26;0.99]$\\
Wykształcenie średnie& $0.42[0.22;0.80]$\\
Wykształcenie wyższe& $0.45[0.22;0.92]$\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img293c66232b211018957d259498fcf4db.png)
Szansa na wystąpienie badanej wady w każdej kategorii wykształcenia odnoszona jest zawsze do szansy wystąpienia wady przy wykształceniu podstawowym. Widzimy, że dla bardziej wykształconych matek, iloraz szans jest niższy. Dla matki z wykształceniem:
- zawodowym szansa wystąpienia wady u dziecka stanowi 0.51 część szansy na urodzenie dziecka z wadą jaką ma matka z wykształceniem podstawowym;
- średnim szansa wystąpienia wady u dziecka stanowi 0.42 część szansy na urodzenie dziecka z wadą jaką ma matka z wykształceniem podstawowym;
- wyższym szansa wystąpienia wady u dziecka stanowi 0.45 część szansy na urodzenie dziecka z wadą jaką ma matka z wykształceniem podstawowym.
Przeprowadzono eksperyment mający na celu zbadanie umiejętność koncentracji grupy dorosłych podczas sytuacji niekomfortowych. W eksperymencie wzięło udział 190 osób (130 osób to zbiór uczący, 40 osób to zbiór testowy). Każda badana osoba dostała pewne zadanie, którego rozwiązanie wymagało skupienia uwagi. Podczas eksperymentu niektóre osoby zostały poddane działaniu czynnika zakłócającego jakim była podwyższona temperatura powietrza do 32 stopni Celsiusza. Osoby biorące udział w eksperymencie zapytano dodatkowo o ich miejsce zamieszkania, płeć, wiek i wykształcenie. Czas na rozwiązanie zadania ograniczono do 45 minut. Dla osób, które skończyły przed czasem odnotowano rzeczywisty czas poświęcony na rozwiązanie. Całość naszych obliczeń wykonamy tylko dla osóbnależących do zbioru uczącego.
Zmienna ROZWIĄZANIE (tak/nie) zawiera wynik eksperymentu, czyli informację o tym, czy zadanie zostało rozwiązane poprawnie czy też nie. Pozostałe zmienne, które mogły wpływać na wynik eksperymentu to:
MIEJSCEZAM (1=miasto/0=wieś),
PŁEĆ (1=kobieta/0=mężczyzna),
WIEK (w latach),
WYKSZTAŁCENIE (1=podstawowe, 2=zawodowe, 3=średnie, 4=wyższe),
CZAS rozwiązywania (w minutach),
ZAKŁÓCENIA (1=tak/0=nie).
Na bazie wszystkich zmiennych zbudowano model regresji logistycznej, gdzie jako stan wyróżniony zmiennej ROZWIĄZANIE wybrano tak.
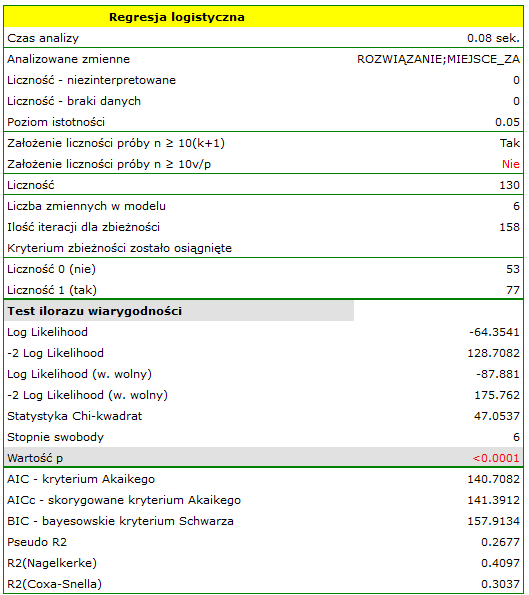
Jakość jego dopasowania opisują współczynniki: 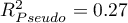 ,
, 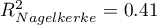 i
i 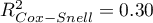 . Na wystarczającą jakość dopasowania wskazuje również wynik testu Hosmera-Lemeshowa
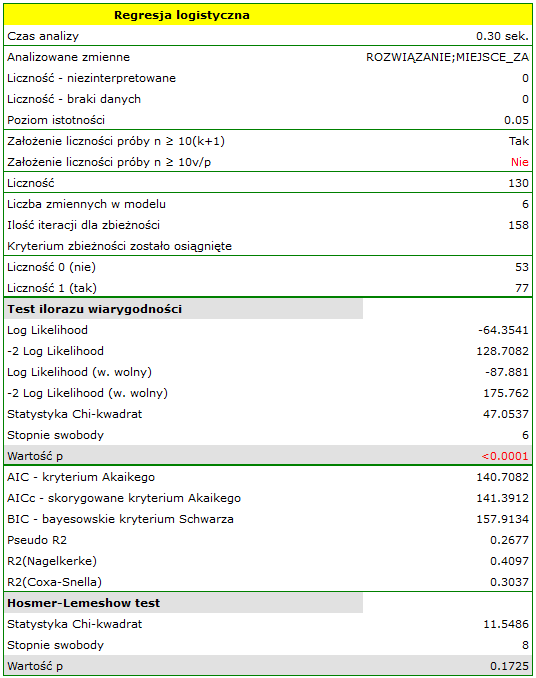
. Na wystarczającą jakość dopasowania wskazuje również wynik testu Hosmera-Lemeshowa 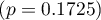 . Cały model jest istotny statystycznie o czym mówi wynik testu ilorazu wiarygodności
. Cały model jest istotny statystycznie o czym mówi wynik testu ilorazu wiarygodności 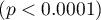 .
.
Wartości obserwowane i prawdopodobieństwo przewidywane możemy zobaczyć na wykresie:

W modelu zmienne, które w sposób istotny wpływają na wynik to:
WIEK: 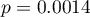 ,
,
CZAS: 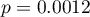 ,
,
ZAKŁÓCENIA: 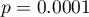 .
.
Przy czym, im osoba rozwiązująca jest młodsza, czas rozwiązywania krótszy i brak jest czynnika zakłócającego, tym większe prawdopodobieństwo poprawnego rozwiązania:
WIEK: ![LaTeX $OR[95\%CI]=0.90[0.85;0.96]$](/lib/exe/fetch.php?media=wiki:latex:/img2d561911e46044388c920f350283e92f.png) ,
,
CZAS: ![LaTeX $OR[95\%CI]=0.91[0.87;0.97]$](/lib/exe/fetch.php?media=wiki:latex:/img856be89e1314daa3623408b907f11c45.png) ,
,
ZAKŁÓCENIA: ![LaTeX $OR[95\%CI]=0.15[0.06;0.37]$](/lib/exe/fetch.php?media=wiki:latex:/img8cb35d4670d9bda19bc8f3dd46b985b3.png) .
.
Uzyskane wyniki Ilorazu Szans przedstawiono na poniższym wykresie:

Jeśli model miałby zostać użyty do prognozowania, to należy przyjrzeć się jakości klasyfikacji. Wyliczamy w tym celu krzywe ROC.
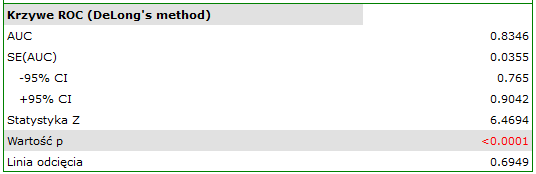

Rezultat wydaje się zadowalający. Pole pod krzywą wynosi 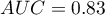 i jest istotnie większe niż
i jest istotnie większe niż 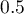
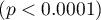 , więc na podstawie zbudowanego modelu można klasyfikować. Proponowany punkt odcięcia dla krzywej ROC wynosi
, więc na podstawie zbudowanego modelu można klasyfikować. Proponowany punkt odcięcia dla krzywej ROC wynosi 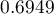 i jest nieco wyższy niż standardowo używany w regresji poziom
i jest nieco wyższy niż standardowo używany w regresji poziom 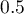 . Klasyfikacja wyznaczona na bazie tego punktu odcięcia daje 79,23% przypadków zaklasyfikowanych poprawnie, z czego poprawnie zaklasyfikowanych wartości „tak” jest 72.73% (czułość), wartości „nie” jest 88.68% (swoistość). Klasyfikacja uzyskana na podstawie standardowej wartości daje nie co mniej, bo 73.85% przypadków zaklasyfikowanych poprawnie, ale uzyskamy dzięki niej więcej poprawnie zaklasyfikowanych wartości „tak” jest 83.12%, choć mniej poprawnie zaklasyfikowanych wartości „nie” jest 60.38%.
. Klasyfikacja wyznaczona na bazie tego punktu odcięcia daje 79,23% przypadków zaklasyfikowanych poprawnie, z czego poprawnie zaklasyfikowanych wartości „tak” jest 72.73% (czułość), wartości „nie” jest 88.68% (swoistość). Klasyfikacja uzyskana na podstawie standardowej wartości daje nie co mniej, bo 73.85% przypadków zaklasyfikowanych poprawnie, ale uzyskamy dzięki niej więcej poprawnie zaklasyfikowanych wartości „tak” jest 83.12%, choć mniej poprawnie zaklasyfikowanych wartości „nie” jest 60.38%.
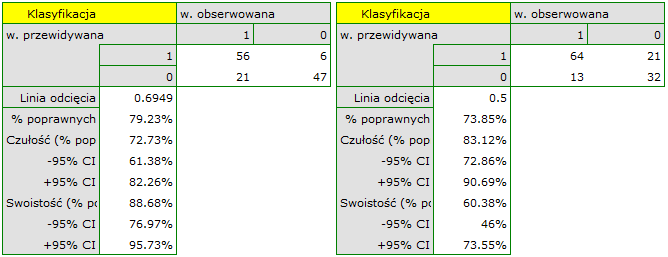
Na tym etapie możemy zakończyć analizę klasyfikacji, lub jeśli wynik nie jest wystarczający bardziej wnikliwą analizę krzywej ROC możemy przeprowadzić w module Krzywa ROC.
Ponieważ uznaliśmy, że klasyfikacja na podstawie modelu jest zadowalająca, możemy wyliczyć prognozowaną wartość zmiennej zależnej dla dowolnie zadanych warunków. Sprawdźmy jakie szanse na rozwiązanie zadania ma osoba dla której:
MIEJSCEZAM (1=miasto),
PŁEĆ (1=kobieta),
WIEK (50 lat),
WYKSZTAŁCENIE (1=podstawowe),
CZAS rozwiązywania (20 minut),
ZAKŁÓCENIA (1=tak).
W tym celu na podstawie wartości współczynnika  wyliczane jest prawdopodobieństwo przewidywane (prawdopodobieństwo uzyskania odpowiedzi
wyliczane jest prawdopodobieństwo przewidywane (prawdopodobieństwo uzyskania odpowiedzi tak pod warunkiem określenia wartości zmiennych zależnych):
![LaTeX \begin{displaymath}
\begin{array}{l}
P(Y=tak|MIEJSCEZAM,PŁEĆ,WIEK,WYKSZTAŁCENIE,CZAS,ZAKŁÓCENIA)=\\[0.2cm]
=\frac{e^{7.23-0.45\textrm{\scriptsize \textit{MIEJSCEZAM}}-0.45\textrm{\scriptsize\textit{PŁEĆ}}-0.1\textrm{\scriptsize\textit{WIEK}}+0.46\textrm{\scriptsize\textit{WYKSZTAŁCENIE}}-0.09\textrm{\scriptsize\textit{CZAS}}-1.92\textrm{\scriptsize\textit{ZAKŁÓCENIA}}}}{1+e^{7.23-0.45\textrm{\scriptsize\textit{MIEJSCEZAM}}-0.45\textrm{\scriptsize\textit{PŁEĆ}}-0.1\textrm{\scriptsize\textit{WIEK}}+0.46\textrm{\scriptsize\textit{WYKSZTAŁCENIE}}-0.09\textrm{\scriptsize\textit{CZAS}}-1.92\textrm{\scriptsize\textit{ZAKŁÓCENIA}}}}=\\[0.2cm]
=\frac{e^{7.231-0.453\cdot1-0.455\cdot1-0.101\cdot50+0.456\cdot1-0.089\cdot20-1.924\cdot1}}{1+e^{7.231-0.453\cdot1-0.455\cdot1-0.101\cdot50+0.456\cdot1-0.089\cdot20-1.924\cdot1}}
\end{array}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img05c978955ec4691a8e7bfe3d265dc858.png)
W rezultacie tych obliczeń program zwróci wynik:
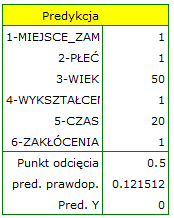
Uzyskane prawdopodobieństwo rozwiązania zadania wynosi 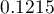 , więc na podstawie punktu odcięcia
, więc na podstawie punktu odcięcia 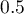 przewidziany wynik to
przewidziany wynik to 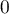 - czyli zadanie nie rozwiązane poprawnie.
- czyli zadanie nie rozwiązane poprawnie.
2021/01/11 22:02
Predykcja na podstawie modelu i walidacja zbioru testowego
Walidacja
Walidacja modelu to sprawdzenie jego jakości. W pierwszej kolejności wykonywana jest na danych, na których model był zbudowany (zbiór uczący), czyli zwracana jest w raporcie opisującym uzyskany model. By można było z większą pewnością osądzić na ile model nadaje się do prognozy nowych danych, ważnym elementem walidacji jest zastosowaniee modelu do danych, które nie były wykorzystywane w estymacji modelu. Jeśli podsumowanie w oparciu o dane uczące będzie satysfakcjonujące tzn. wyznaczane błędy, współczynniki  i kryteria informacyjne będą na zadowalającym nas poziomie, a podsumowanie w oparciu o nowe dane (tzw. zbiór testowy) będzie równie korzystne, wówczas z dużym prawdopodobieństwem można uznać, że taki model nadaje się do predykcji. Dane testujące powinny pochodzić z tej samej populacji, z której były wybrane dane uczące. Często jest tak, że przed przystąpieniem do budowy modelu zbieramy dane, a następnie w sposób losowy dzielimy je na zbiór uczący, czyli dane które posłużą do budowy modelu i zbiór testowy, czyli dane które posłużą do dodatkowej walidacji modelu.
i kryteria informacyjne będą na zadowalającym nas poziomie, a podsumowanie w oparciu o nowe dane (tzw. zbiór testowy) będzie równie korzystne, wówczas z dużym prawdopodobieństwem można uznać, że taki model nadaje się do predykcji. Dane testujące powinny pochodzić z tej samej populacji, z której były wybrane dane uczące. Często jest tak, że przed przystąpieniem do budowy modelu zbieramy dane, a następnie w sposób losowy dzielimy je na zbiór uczący, czyli dane które posłużą do budowy modelu i zbiór testowy, czyli dane które posłużą do dodatkowej walidacji modelu.
Okno z ustawieniami opcji walidacji wywołujemy poprzez menu Statystyki zaawansowane→Modele wielowymiarowe→Regresja logistyczna - predykcja/walidacja.
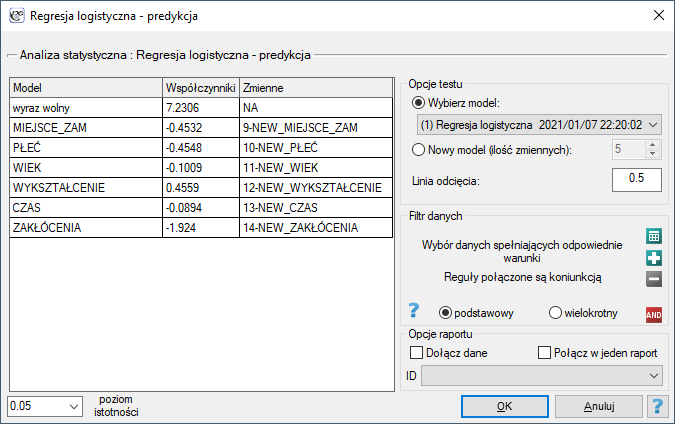
By dokonać walidacji należy wskazać model, na podstawie którego chcemy jej dokonać. Walidacji możemy dokonać na bazie:
- zbudowanego w PQStat modelu regresji logistycznej - wystarczy wybrać model spośród modeli przypisanych do danego arkusza, a liczba zmiennych i współczynniki modelu zostaną ustawione automatycznie; zbiór testowy powinien się znaleźć w tym samym arkuszu co zbiór uczący;
- modelu nie zbudowanego w programie PQStat, ale uzyskanego z innego źródła (np. opisanego w przeczytanej przez nas pracy naukowej) - w oknie analizy należy podać liczbę zmiennych oraz wpisać współczynniki dotyczące każdej z nich.
W oknie analizy należy wskazać te nowe zmienne, które powinny zostać wykorzystane do walidacji.
Predykcja
Najczęściej ostatnim etapem analizy regresji jest wykorzystanie zbudowanego i uprzednio zweryfikowanego modelu do predykcji.
- Predykcja dla jednego obiektu może być wykonywana wraz z budową modelu, czyli w oknie analizy
Statystyki zaawansowane→Modele wielowymiarowe→Regresja logistyczna, - Predykcja dla większej grupy nowych danych jest wykonywana poprzez menu
Statystyki zaawansowane→Modele wielowymiarowe→Regresja logistyczna - predykcja/walidacja.
By dokonać predykcji należy wskazać model, na podstawie którego chcemy jej dokonać. Predykcji możemy dokonać na bazie:
- zbudowanego w PQStat modelu regresji logistycznej - wystarczy wybrać model spośród modeli przypisanych do danego arkusza, a liczba zmiennych i współczynniki modelu zostaną ustawione automatycznie; zbiór testowy powinien się znaleźć w tym samym arkuszu co zbiór uczący;
- modelu nie zbudowanego w programie PQStat, ale uzyskanego z innego źródła (np. opisanego w przeczytanej przez nas pracy naukowej) - w oknie analizy należy podać liczbę zmiennych oraz wpisać współczynniki dotyczące każdej z nich.
W oknie analizy należy wskazać te nowe zmienne, które powinny zostać wykorzystane do predykcji.
Na podstawie nowych danych wyznaczana jest wartość prawdopodobieństwa przewidywanego przez model a następnie predykacja wystąpienia zdarzenia (1) lub jego braku (0). Punkt odcięcia, na podstawie którego wykonywana jest klasyfikacja to domyślnie wartość 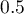 . Użytkownik może zmienić tę wartość na dowolną wartość z przedziału
. Użytkownik może zmienić tę wartość na dowolną wartość z przedziału 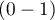 np. wartość sugerowaną przez krzywą ROC.
np. wartość sugerowaną przez krzywą ROC.
Przykład c.d. (plik zadanie.pqs)
W eksperymencie badającym umiejętność koncentracji, dla grupy 130 osób zbioru uczącego, zbudowano model regresji logistycznej w oparciu o następujące zmienne:
zmienna zależna: ROZWIĄZANIE (tak/nie) - informacja o tym, czy zadanie zostało rozwiązane poprawnie czy też nie;
zmienne niezależne:
MIEJSCEZAM (1=miasto/0=wieś),
PŁEĆ (1=kobieta/0=mężczyzna),
WIEK (w latach),
WYKSZTAŁCENIE (1=podstawowe, 2=zawodowe, 3=średnie, 4=wyższe),
CZAS rozwiązywania (w minutach),
ZAKŁÓCENIA (1=tak/0=nie).
Jednak tylko cztery zmienne: WIEK, WYKSZTAŁCENIE, CZAS rozwiązywania i ZAKŁÓCENIA, wnoszą istotne informacje do modelu. Zbudujemy model dla danych zbioru uczącego w oparciu o te cztery zmienne a następnie, by się upewnić że będzie działał poprawnie, zwalidujemy go na testowym zbierze danych. Jeśli model przejdzie tę próbę, to będziemy go stosować do predykcji dla nowych osób. By korzystać z odpowiednich zbiorów ustawiamy każdorazowo filtr danych.
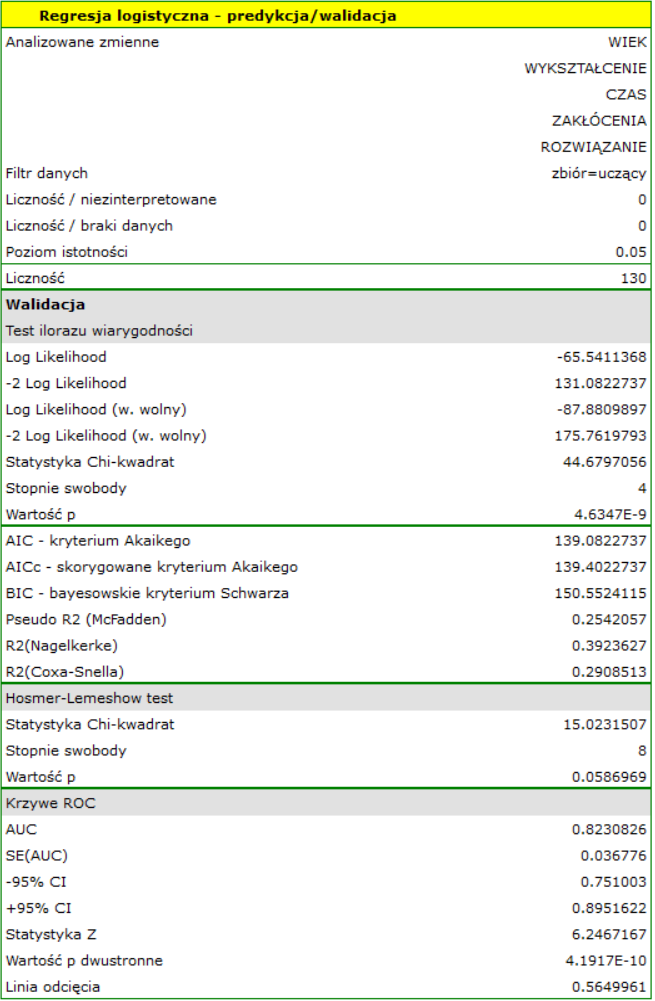
Dla zbioru uczącego wartości opisujące jakość dopasowania modelu nie są bardzo wysokie 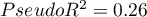 a
a 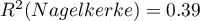 , ale już jakość jego predykcji jest zadowalająca (AUC[95%CI]=0.82[0.75, 0.90], czułość =82%, swoistość 60%).
, ale już jakość jego predykcji jest zadowalająca (AUC[95%CI]=0.82[0.75, 0.90], czułość =82%, swoistość 60%).
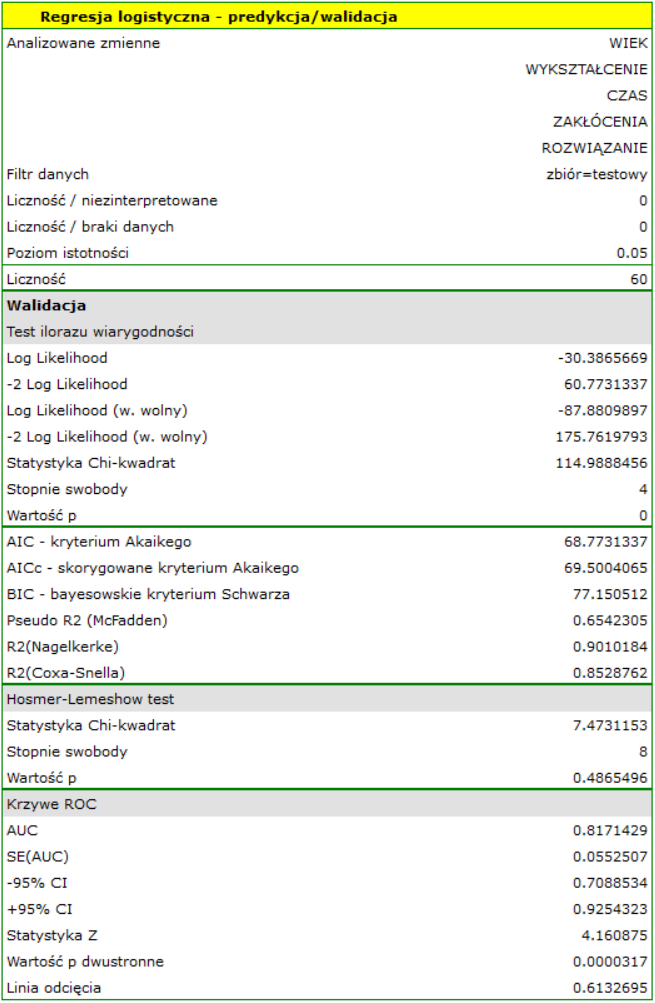
Dla zbioru testowego wartości opisujące jakość dopasowania modelu są nawet wyższe niż dla danych uczących 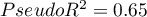 a
a 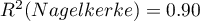 . Jakość predykcji dla danych testowych jest wciąż zadowalająca (AUC[95%CI]=0.82[0.71, 0.93], czułość =73%, swoistość 64%), dlatego użyjemy modelu do predykcji. W tym celu skorzystamy z danych trzech nowych osób dopisanych na końcu zbioru. Wybierzemy opcję
. Jakość predykcji dla danych testowych jest wciąż zadowalająca (AUC[95%CI]=0.82[0.71, 0.93], czułość =73%, swoistość 64%), dlatego użyjemy modelu do predykcji. W tym celu skorzystamy z danych trzech nowych osób dopisanych na końcu zbioru. Wybierzemy opcję Predykcja, ustawimy filtr na nowy zbiór danych i użyjemy naszego modelu do tego by przewidzieć czy dana osoba rozwiąże zadanie poprawnie (uzyska wartość 1) czy też niepoprawnie (uzyska wartość 0).
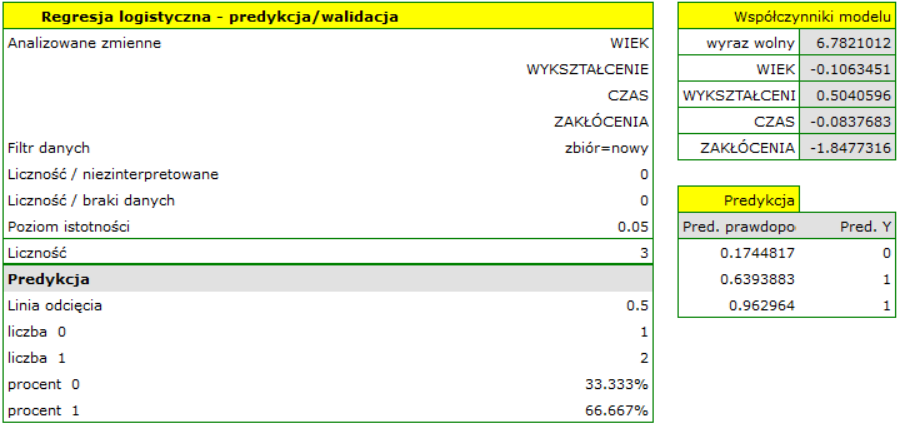
Okazuję się, że prognoza dla pierwszej osoby jest negatywna, a dla dwóch kolejnych pozytywna. Prognoza dla 50-letniej kobiety z wykształceniem podstawowym rozwiązującej test podczas zakłóceń w czasie 20 min wynosi 0.17, co oznacza że prognozujemy iż rozwiąze ona zadanie niepoprawnie, podczas gdy pronoza dla kobiety o 20 lat młodszej jest już korzystna - prawdopodobieństwo rozwiązania przez nią zadania wynosi 0.64. Największe prawdopodobieństwo (równe 0.96) poprawnego rozwiazania ma trzecia kobieta, która rozwiązywała test w ciągu 10 minut i bez zakłuceń.
Gdybyśmy chcieli postawić prognozę na podstawie innego modelu (np. uzyskanego podczas innego badania naukowego: ROZWIĄZANIE=6-0.1*WIEK+0.5*WYKSZT-0.1*CZAS-2*ZAKŁÓCENIA) - wystrczy, że w oknie analizy wybierzemy nowy model, ustawimy jego współczynniki i porgnozę dla wybraych osób można powtórzyć w oparciu o ten model.
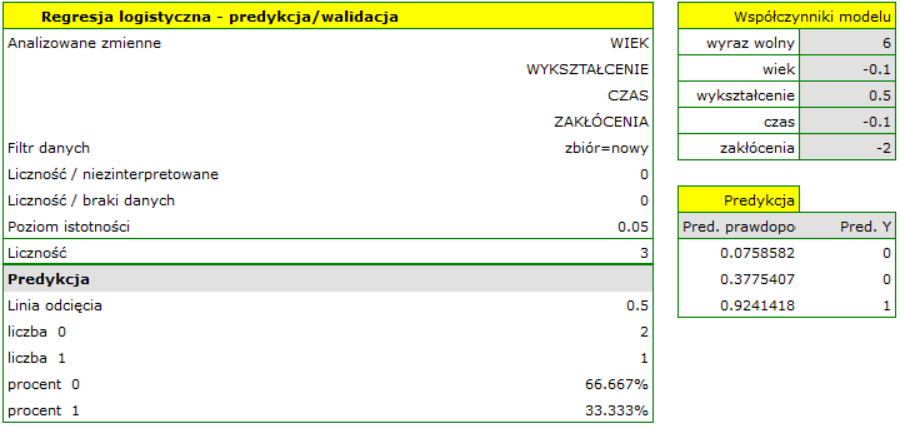
Tym razem, zgodnie z prognozą nowego modelu, przewidywania dla pierwszej i drugiej osoby są negatywne, a trzeciej pozytywne.
2021/01/11 22:02
1)
Peduzzi P., Concato J., Kemper E., Holford T.R., Feinstein A.R. (1996), A simulation study of the number of events per variable in logistic regression analysis. J Clin Epidemiol;49(12):1373-9
pl/statpqpl/wielowympl/logistpl.txt · ostatnio zmienione: 2023/03/31 18:48 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

