Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
Action disabled: source
statpqpl:porown2grpl:nparpl:chikwcxrpl
Test chi-kwadrat dla dużych tabel
Test ten opierają się na danych zebranych w postaci tabeli kontyngencji 2 cech ( ,
,  ), z których pierwsza ma możliwe
), z których pierwsza ma możliwe  kategorii
kategorii 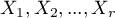 a druga
a druga  kategorii
kategorii 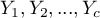 .
.
Test  dla tabel
dla tabel 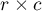 znany jest również pod nazwą testu
znany jest również pod nazwą testu  Pearsona (ang. Pearson's Chi-square test), Karl Pearson 1900. Test ten jest rozszerzeniem na 2 cechy testu chi-kwadrat (dobroci dopasowania).
Statystyka testowa ma postać:
Pearsona (ang. Pearson's Chi-square test), Karl Pearson 1900. Test ten jest rozszerzeniem na 2 cechy testu chi-kwadrat (dobroci dopasowania).
Statystyka testowa ma postać:
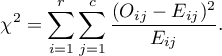
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru: 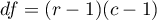 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności poziomem istotności
porównujemy z poziomem istotności poziomem istotności  .
.
Okno z ustawieniami opcji testu Chi-kwadrat (RxC) wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Chi-kwadrat, Fisher, OR/RR lub poprzez ''Kreator''.
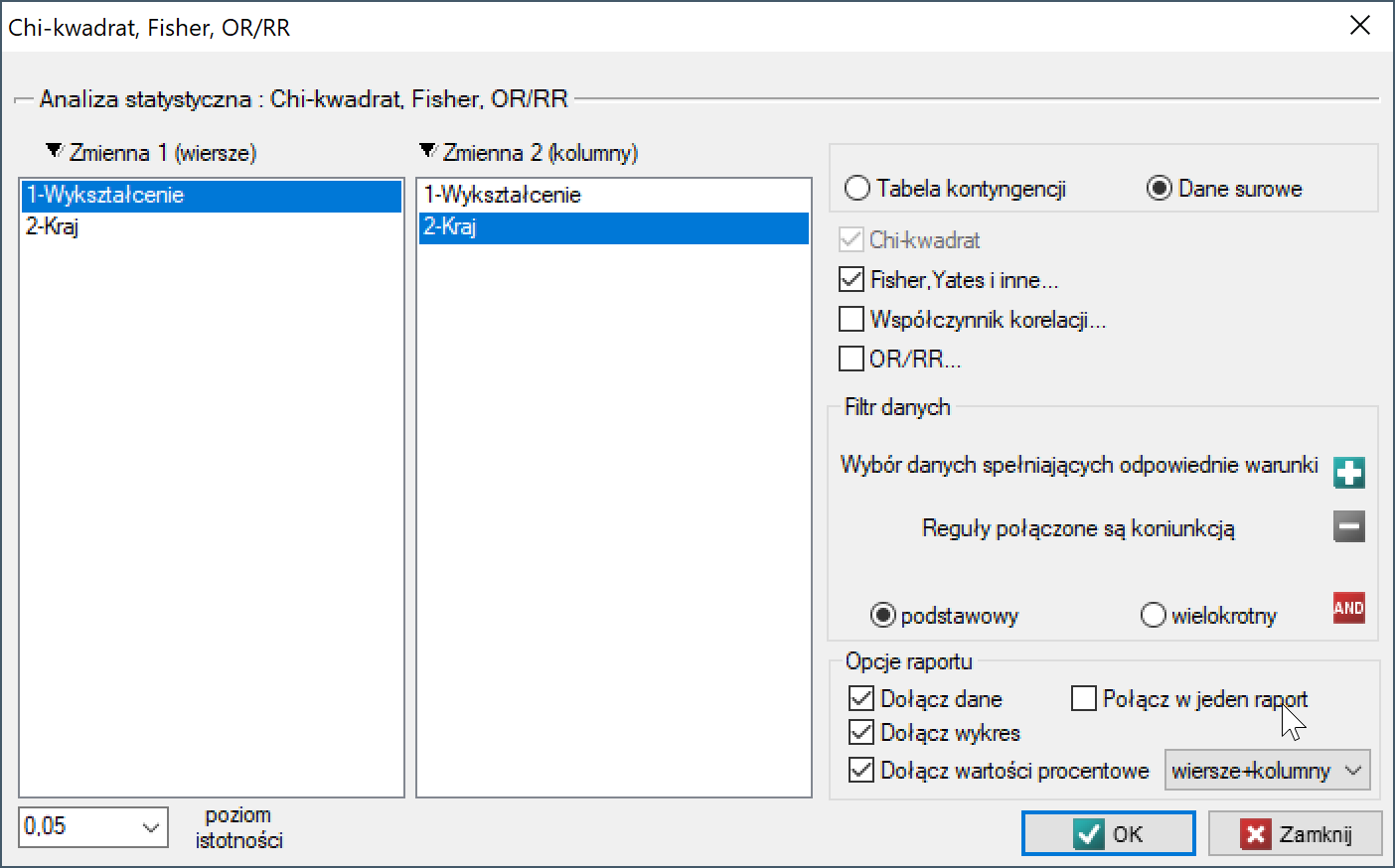
Przykład (plik kraj-wykształcenie.pqs)
Rozpatrujemy próbę 605 osób (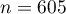 ), dla których badamy 2 cechy (
), dla których badamy 2 cechy ( =kraj zamieszkania,
=kraj zamieszkania,  =wykształcenie). Pierwsza cecha występuje w 4, a druga w 3 kategoriach (
=wykształcenie). Pierwsza cecha występuje w 4, a druga w 3 kategoriach ( =Kraj 1,
=Kraj 1,  =Kraj 2,
=Kraj 2, 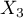 =Kraj 3,
=Kraj 3, 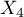 =Kraj 4,
=Kraj 4, 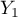 =podstawowe,
=podstawowe, 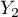 =średnie,
=średnie, 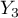 =wyższe). Rozkład danych przedstawia tabela kontyngencji:
=wyższe). Rozkład danych przedstawia tabela kontyngencji:
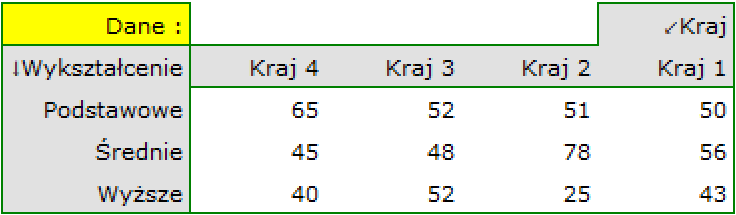
Na podstawie tej próby chcielibyśmy się dowiedzieć, czy w badanej populacji istnieje zależność pomiędzy wykształceniem a krajem zamieszkania.
Hipotezy:
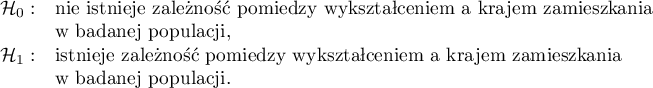
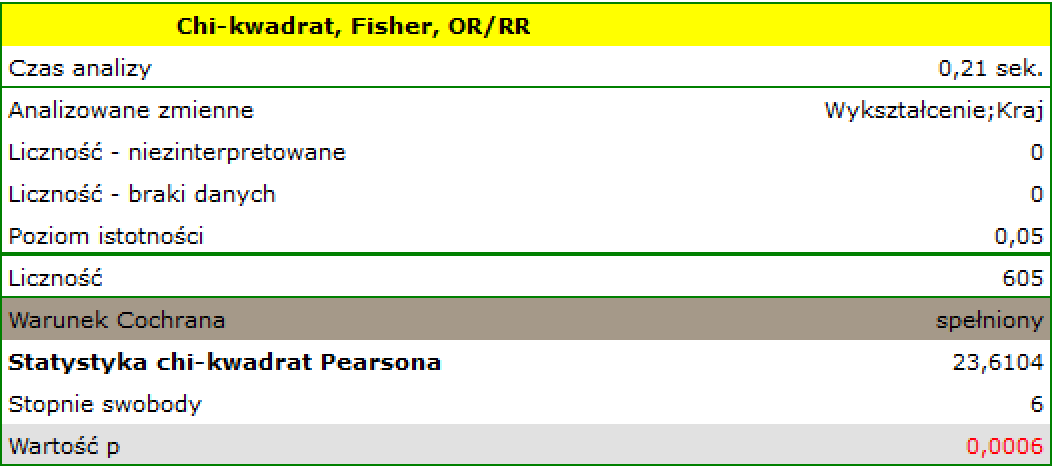
Warunek Cochrana jest spełniony.
Wartość 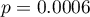 . Zatem na poziomie istotności
. Zatem na poziomie istotności  możemy powiedzieć, że istniej zależność pomiędzy krajem zamieszkania a wykształceniem w badanej populacji.
możemy powiedzieć, że istniej zależność pomiędzy krajem zamieszkania a wykształceniem w badanej populacji.
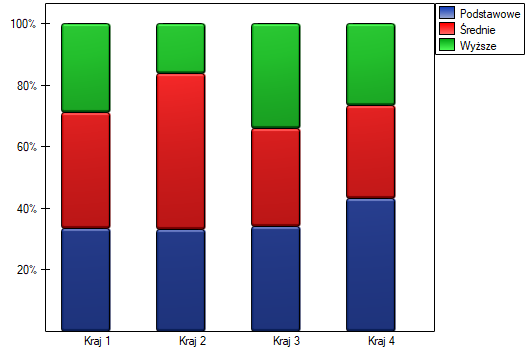
Jeśli interesują nas dokładniejsze informacje na temat wykrytych zależności, uzyskamy je wyznaczając porównania wielokrotne poprzez opcje Fisher, Yates i inne… a następnie Wielokrotne porównania kolumn (RxC) i jedną z poprawek np. Benjamini-Hochberg
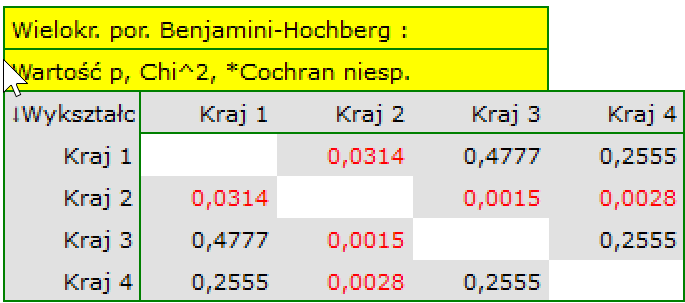
Dokładniejsza analiza pozwala stwierdzić, że jedynie drugi kraj różni się poziomem wykształcenia od pozostałych krajów w sposób istotny statystycznie.
statpqpl/porown2grpl/nparpl/chikwcxrpl.txt · ostatnio zmienione: 2021/02/27 18:16 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


