Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
pl:statpqpl:wielowympl:logistpl:pred
Predykcja na podstawie modelu i walidacja zbioru testowego
Walidacja
Walidacja modelu to sprawdzenie jego jakości. W pierwszej kolejności wykonywana jest na danych, na których model był zbudowany (zbiór uczący), czyli zwracana jest w raporcie opisującym uzyskany model. By można było z większą pewnością osądzić na ile model nadaje się do prognozy nowych danych, ważnym elementem walidacji jest zastosowaniee modelu do danych, które nie były wykorzystywane w estymacji modelu. Jeśli podsumowanie w oparciu o dane uczące będzie satysfakcjonujące tzn. wyznaczane błędy, współczynniki  i kryteria informacyjne będą na zadowalającym nas poziomie, a podsumowanie w oparciu o nowe dane (tzw. zbiór testowy) będzie równie korzystne, wówczas z dużym prawdopodobieństwem można uznać, że taki model nadaje się do predykcji. Dane testujące powinny pochodzić z tej samej populacji, z której były wybrane dane uczące. Często jest tak, że przed przystąpieniem do budowy modelu zbieramy dane, a następnie w sposób losowy dzielimy je na zbiór uczący, czyli dane które posłużą do budowy modelu i zbiór testowy, czyli dane które posłużą do dodatkowej walidacji modelu.
i kryteria informacyjne będą na zadowalającym nas poziomie, a podsumowanie w oparciu o nowe dane (tzw. zbiór testowy) będzie równie korzystne, wówczas z dużym prawdopodobieństwem można uznać, że taki model nadaje się do predykcji. Dane testujące powinny pochodzić z tej samej populacji, z której były wybrane dane uczące. Często jest tak, że przed przystąpieniem do budowy modelu zbieramy dane, a następnie w sposób losowy dzielimy je na zbiór uczący, czyli dane które posłużą do budowy modelu i zbiór testowy, czyli dane które posłużą do dodatkowej walidacji modelu.
Okno z ustawieniami opcji walidacji wywołujemy poprzez menu Statystyki zaawansowane→Modele wielowymiarowe→Regresja logistyczna - predykcja/walidacja.
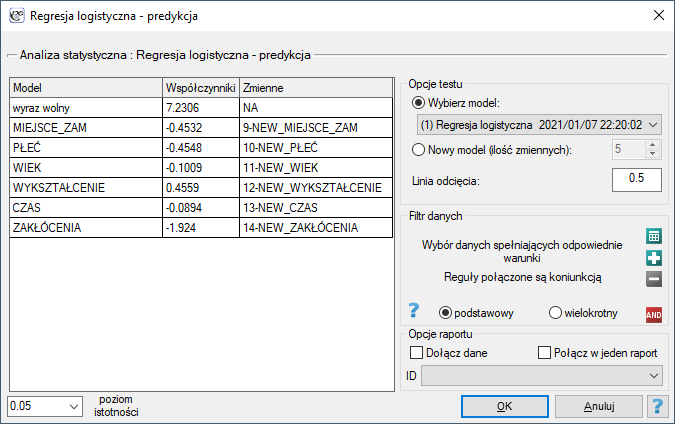
By dokonać walidacji należy wskazać model, na podstawie którego chcemy jej dokonać. Walidacji możemy dokonać na bazie:
- zbudowanego w PQStat modelu regresji logistycznej - wystarczy wybrać model spośród modeli przypisanych do danego arkusza, a liczba zmiennych i współczynniki modelu zostaną ustawione automatycznie; zbiór testowy powinien się znaleźć w tym samym arkuszu co zbiór uczący;
- modelu nie zbudowanego w programie PQStat, ale uzyskanego z innego źródła (np. opisanego w przeczytanej przez nas pracy naukowej) - w oknie analizy należy podać liczbę zmiennych oraz wpisać współczynniki dotyczące każdej z nich.
W oknie analizy należy wskazać te nowe zmienne, które powinny zostać wykorzystane do walidacji.
Predykcja
Najczęściej ostatnim etapem analizy regresji jest wykorzystanie zbudowanego i uprzednio zweryfikowanego modelu do predykcji.
- Predykcja dla jednego obiektu może być wykonywana wraz z budową modelu, czyli w oknie analizy
Statystyki zaawansowane→Modele wielowymiarowe→Regresja logistyczna, - Predykcja dla większej grupy nowych danych jest wykonywana poprzez menu
Statystyki zaawansowane→Modele wielowymiarowe→Regresja logistyczna - predykcja/walidacja.
By dokonać predykcji należy wskazać model, na podstawie którego chcemy jej dokonać. Predykcji możemy dokonać na bazie:
- zbudowanego w PQStat modelu regresji logistycznej - wystarczy wybrać model spośród modeli przypisanych do danego arkusza, a liczba zmiennych i współczynniki modelu zostaną ustawione automatycznie; zbiór testowy powinien się znaleźć w tym samym arkuszu co zbiór uczący;
- modelu nie zbudowanego w programie PQStat, ale uzyskanego z innego źródła (np. opisanego w przeczytanej przez nas pracy naukowej) - w oknie analizy należy podać liczbę zmiennych oraz wpisać współczynniki dotyczące każdej z nich.
W oknie analizy należy wskazać te nowe zmienne, które powinny zostać wykorzystane do predykcji.
Na podstawie nowych danych wyznaczana jest wartość prawdopodobieństwa przewidywanego przez model a następnie predykacja wystąpienia zdarzenia (1) lub jego braku (0). Punkt odcięcia, na podstawie którego wykonywana jest klasyfikacja to domyślnie wartość 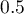 . Użytkownik może zmienić tę wartość na dowolną wartość z przedziału
. Użytkownik może zmienić tę wartość na dowolną wartość z przedziału 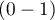 np. wartość sugerowaną przez krzywą ROC.
np. wartość sugerowaną przez krzywą ROC.
Przykład c.d. (plik zadanie.pqs)
W eksperymencie badającym umiejętność koncentracji, dla grupy 130 osób zbioru uczącego, zbudowano model regresji logistycznej w oparciu o następujące zmienne:
zmienna zależna: ROZWIĄZANIE (tak/nie) - informacja o tym, czy zadanie zostało rozwiązane poprawnie czy też nie;
zmienne niezależne:
MIEJSCEZAM (1=miasto/0=wieś),
PŁEĆ (1=kobieta/0=mężczyzna),
WIEK (w latach),
WYKSZTAŁCENIE (1=podstawowe, 2=zawodowe, 3=średnie, 4=wyższe),
CZAS rozwiązywania (w minutach),
ZAKŁÓCENIA (1=tak/0=nie).
Jednak tylko cztery zmienne: WIEK, WYKSZTAŁCENIE, CZAS rozwiązywania i ZAKŁÓCENIA, wnoszą istotne informacje do modelu. Zbudujemy model dla danych zbioru uczącego w oparciu o te cztery zmienne a następnie, by się upewnić że będzie działał poprawnie, zwalidujemy go na testowym zbierze danych. Jeśli model przejdzie tę próbę, to będziemy go stosować do predykcji dla nowych osób. By korzystać z odpowiednich zbiorów ustawiamy każdorazowo filtr danych.
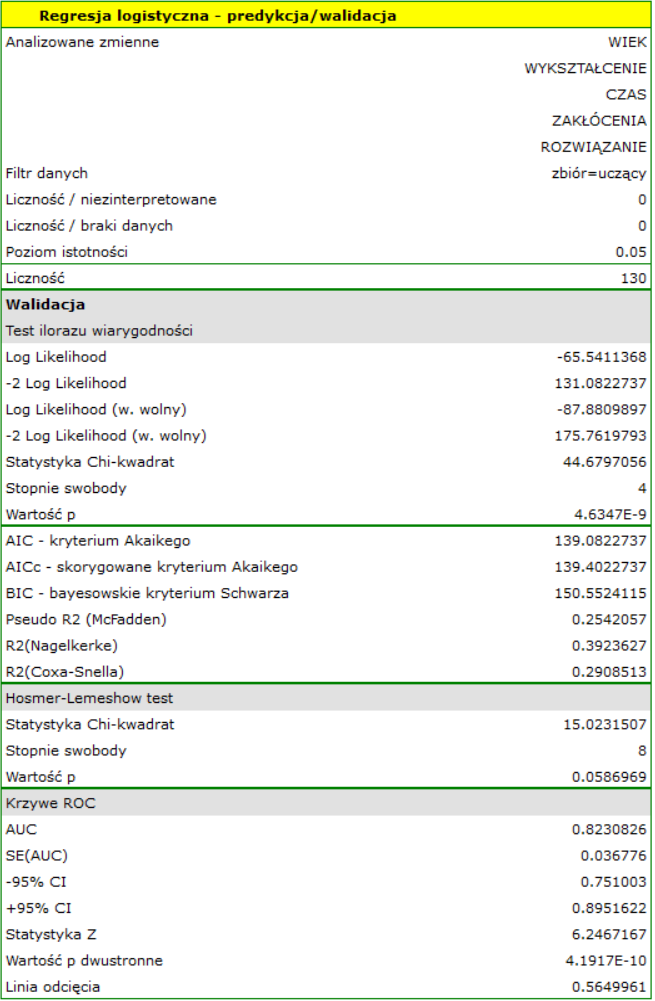
Dla zbioru uczącego wartości opisujące jakość dopasowania modelu nie są bardzo wysokie 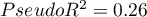 a
a 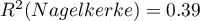 , ale już jakość jego predykcji jest zadowalająca (AUC[95%CI]=0.82[0.75, 0.90], czułość =82%, swoistość 60%).
, ale już jakość jego predykcji jest zadowalająca (AUC[95%CI]=0.82[0.75, 0.90], czułość =82%, swoistość 60%).
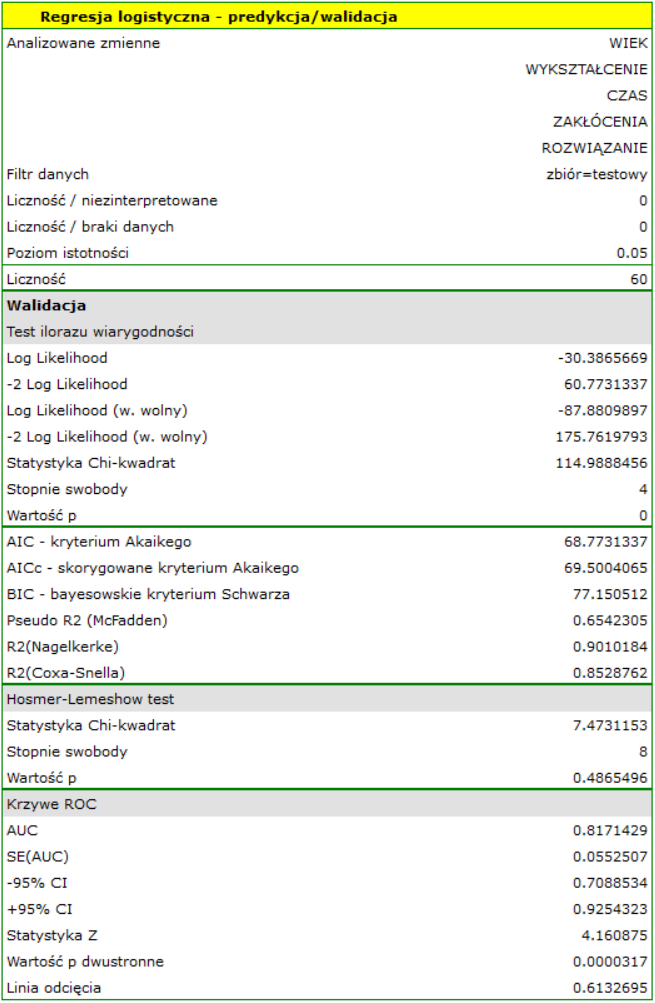
Dla zbioru testowego wartości opisujące jakość dopasowania modelu są nawet wyższe niż dla danych uczących 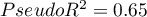 a
a  . Jakość predykcji dla danych testowych jest wciąż zadowalająca (AUC[95%CI]=0.82[0.71, 0.93], czułość =73%, swoistość 64%), dlatego użyjemy modelu do predykcji. W tym celu skorzystamy z danych trzech nowych osób dopisanych na końcu zbioru. Wybierzemy opcję
. Jakość predykcji dla danych testowych jest wciąż zadowalająca (AUC[95%CI]=0.82[0.71, 0.93], czułość =73%, swoistość 64%), dlatego użyjemy modelu do predykcji. W tym celu skorzystamy z danych trzech nowych osób dopisanych na końcu zbioru. Wybierzemy opcję Predykcja, ustawimy filtr na nowy zbiór danych i użyjemy naszego modelu do tego by przewidzieć czy dana osoba rozwiąże zadanie poprawnie (uzyska wartość 1) czy też niepoprawnie (uzyska wartość 0).
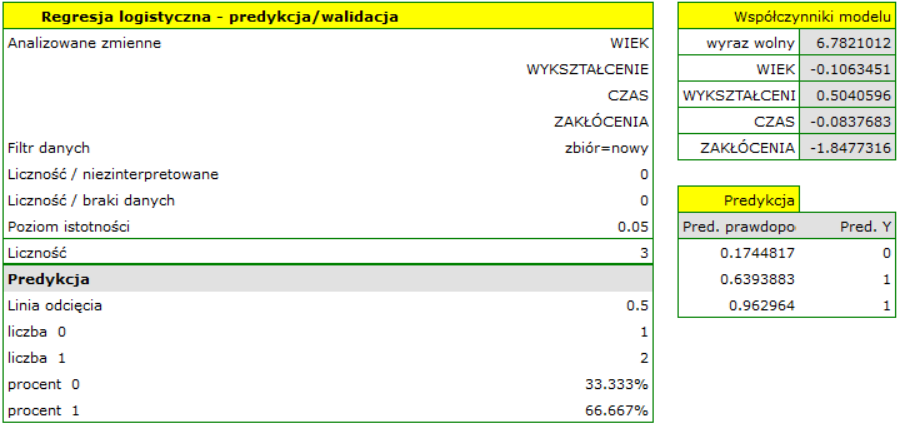
Okazuję się, że prognoza dla pierwszej osoby jest negatywna, a dla dwóch kolejnych pozytywna. Prognoza dla 50-letniej kobiety z wykształceniem podstawowym rozwiązującej test podczas zakłóceń w czasie 20 min wynosi 0.17, co oznacza że prognozujemy iż rozwiąze ona zadanie niepoprawnie, podczas gdy pronoza dla kobiety o 20 lat młodszej jest już korzystna - prawdopodobieństwo rozwiązania przez nią zadania wynosi 0.64. Największe prawdopodobieństwo (równe 0.96) poprawnego rozwiazania ma trzecia kobieta, która rozwiązywała test w ciągu 10 minut i bez zakłuceń.
Gdybyśmy chcieli postawić prognozę na podstawie innego modelu (np. uzyskanego podczas innego badania naukowego: ROZWIĄZANIE=6-0.1*WIEK+0.5*WYKSZT-0.1*CZAS-2*ZAKŁÓCENIA) - wystrczy, że w oknie analizy wybierzemy nowy model, ustawimy jego współczynniki i porgnozę dla wybraych osób można powtórzyć w oparciu o ten model.
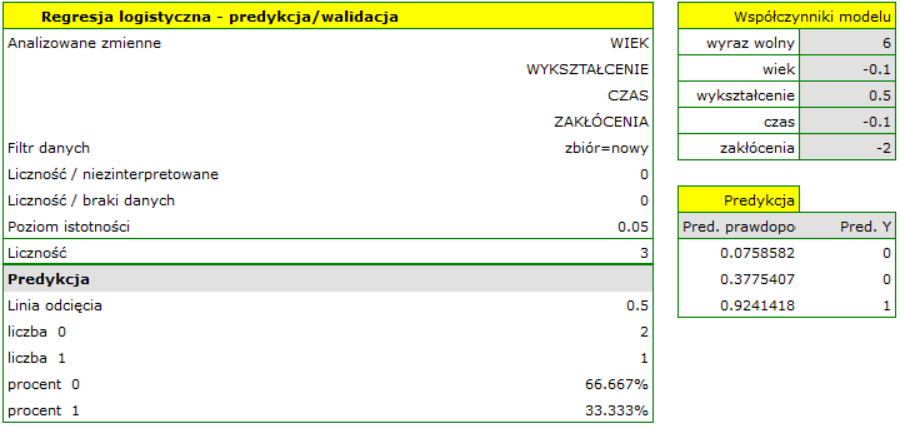
Tym razem, zgodnie z prognozą nowego modelu, przewidywania dla pierwszej i drugiej osoby są negatywne, a trzeciej pozytywne.
pl/statpqpl/wielowympl/logistpl/pred.txt · ostatnio zmienione: 2023/03/31 19:09 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

