Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Baza Wiedzy » statpqpl » Redukcja wymiarów i grupowanie » Analiza skupień » Metody hierarchiczne
Pasek boczny
pl:statpqpl:redpl:skupienpl:hierarchpl
Metody hierarchiczne
Metody hierarchicznej analizy skupień polegają na budowaniu hierarchii skupień poczynając od tych najmniejszych (złożonych z pojedynczych obiektów), a kończąc na tych największych (złożonych z maksymalnej liczby obiektów). Skupienia tworzone są na bazie macierzy podobieństwa obiektów.
PROCEDURA AGLOMERACYJNA
- Postępując zgodnie z wskazaną metodą wiązania, algorytm znajduje w macierzy podobieństwa parę podobnych obiektów i łączy je w skupienie;
- Wymiar macierzy podobieństwa zostaje zredukowany o jeden (dwa obiekty zastąpiono jednym) a odległości znajdujące się w macierzy wyliczone są ponownie;
- Kroki 2-3 są powtarzane aż do uzyskania jednego skupienia zawierającego wszystkie obiekty.
Podobieństwo obiektów
W toku prac związanych z analizą skupień zasadniczą rolę odgrywają miary podobieństwa lub odległości. Wzajemne podobieństwo obiektów umieszczane jest w macierzy podobieństwa. Duża różnorodność metod wyznaczania odległości/niepodobieństwa między obiektami pozwala na wybór takich miar, które najlepiej odzwierciedlają rzeczywiste relacje. Szerzej miary odległości i podobieństwa opisane są w dziale Macierz podobieństwa.
Analiza skupień opiera swoje działania na wyszukiwaniu skupień wewnątrz macierzy podobieństwa. Macierz taka jest budowana w trakcie wykonywania analizy skupień. By analiza skupień przyniosła pożądane skutki, przy wyborze sposobu wyliczania odległości należy pamiętać, że większe wartości liczbowe w macierzy podobieństwa mają wskazywać na większe zróżnicowanie obiektów, a wartości mniejsze na ich podobieństwo.
Uwaga! By zwiększyć wpływ wybranych zmiennych na elementy macierzy podobieństwa, należy wskazać odpowiednie wagi przy ustawianiu sposobu definiowania odległości pamiętając jednocześnie o wystandaryzowaniu danych. Np. Dla osób chcących zaopiekować się psem pogrupowanie psów zgodnie z wielkością, umaszczeniem, długością ogona, charakterem, rasą itp. ułatwi dokonanie wyboru. Jednak, identyczne traktowanie wszystkich cech może spowodować umieszczenie zupełnie niepodobnych psów w jednej grupie. Natomiast dla większości z nas ważniejsza jest wielkość psa i jego charakter niż długość jego ogona, dlatego w grupowaniu należałoby ustawić miary podobieństwa tak, by to właśnie wielkość i charakter miały największe znaczenie w budowaniu skupień.
Metody wiązania obiektów i skupień
- Metoda pojedynczego wiązania (najbliższe sąsiedztwo) - odległość pomiędzy skupieniami określona jest poprzez odległość tych obiektów każdego skupienia, które znajdują się najbliżej siebie.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psline{-}(1.7,0.1)(5.1,-0.4)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imge1a5de3e36c331f92bb1ddd197ffcc63.png)
- Metoda pełnego wiązania (najdalsze sąsiedztwo) - odległość pomiędzy skupieniami określona jest poprzez odległość tych obiektów każdego skupienia, które znajdują się najdalej siebie.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psline{-}(-.8,1)(7.2,1.2)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/imgd86738754d560f3b0b517c3b97807da1.png)
- Metoda średnich połączeń - odległość pomiędzy skupieniami określona jest poprzez średnią odległość pomiędzy wszystkimi parami obiektów zlokalizowanych w obrębie dwóch różnych skupień.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psline{-}(-.8,1)(7.2,1.2)
\psline{-}(-.8,1)(5.1,-0.4)
\psline{-}(-.8,1)(5.6,1.3)
\psline{-}(1.7,0.1)(7.2,1.2)
\psline{-}(1.7,0.1)(5.1,-0.4)
\psline{-}(1.7,0.1)(5.6,1.3)
\psline{-}(0.6,1.2)(7.2,1.2)
\psline{-}(0.6,1.2)(5.1,-0.4)
\psline{-}(1.7,0.1)(5.6,1.3)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img74722956ba453f9c18004ab4885a71f4.png)
- Metoda średnich połączeń ważonych - analogicznie do metody średnich połączeń polega na wyliczeniu średniej odległości, ale średnia ta ważona jest poprzez liczbę elementów każdego skupienia. W rezultacie powinniśmy wybierać tę metodę, gdy oczekujemy uzyskać skupienia o podobnych licznościach.
- Metoda Warda - opiera się na zasadzie analizy wariancji - wylicza różnicę między sumami kwadratów odchyleń odległości poszczególnych obiektów od środka ciężkości skupienia, do których te obiekty należą. Metoda ta wybierana jest najczęściej ze względu na jej dość uniwersalny charakter.
{2}
\psdot[dotstyle=*](-.8,1)
\psdot[dotstyle=*](1.7,0.1)
\psdot[dotstyle=*](0.6,1.2)
\psline[linestyle=dashed]{-}(-.8,1)(0.52,0.8)
\psline[linestyle=dashed]{-}(1.7,0.1)(0.52,0.8)
\psline[linestyle=dashed]{-}(0.6,1.2)(0.52,0.8)
\psdot[dotstyle=pentagon*,linecolor=red](0.52,0.8)
\pscircle[linewidth=2pt](6,.5){2}
\psdot[dotstyle=*](7.2,1.2)
\psdot[dotstyle=*](5.1,-0.4)
\psdot[dotstyle=*](5.6,1.3)
\psdot[dotstyle=pentagon*,linecolor=red](5.85,0.8)
\psline[linestyle=dashed]{-}(7.2,1.2)(5.85,0.8)
\psline[linestyle=dashed]{-}(5.1,-0.4)(5.85,0.8)
\psline[linestyle=dashed]{-}(5.6,1.3)(5.85,0.8)
\psline[linestyle=dotted]{-}(0.52,0.8)(5.85,0.8)
\psline[linestyle=dotted]{-}(-.8,1)(7.2,1.2)
\psline[linestyle=dotted]{-}(-.8,1)(5.1,-0.4)
\psline[linestyle=dotted]{-}(-.8,1)(5.6,1.3)
\psline[linestyle=dotted]{-}(1.7,0.1)(7.2,1.2)
\psline[linestyle=dotted]{-}(1.7,0.1)(5.1,-0.4)
\psline[linestyle=dotted]{-}(1.7,0.1)(5.6,1.3)
\psline[linestyle=dotted]{-}(0.6,1.2)(7.2,1.2)
\psline[linestyle=dotted]{-}(0.6,1.2)(5.1,-0.4)
\psline[linestyle=dotted]{-}(1.7,0.1)(5.6,1.3)
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img169789b519f1a291561b77a1301c7fc1.png)
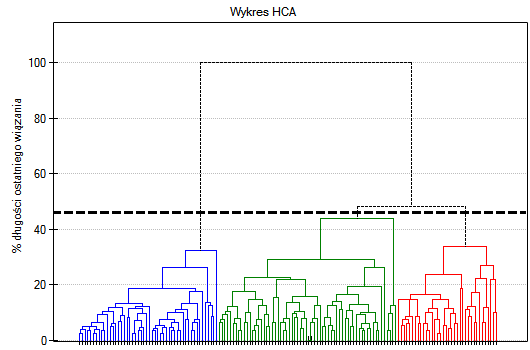
Wynik analizy skupień prowadzonej metodą hierarchiczną przedstawia się przy pomocy dendogramu. Dendogram jest formą drzewa wskazującego związki pomiędzy poszczególnymi obiektami uzyskane z analizy macierzy podobieństwa. Poziom odcięcia dendogramu decyduje o liczbie skupień, na które chcemy dzielić zgromadzone obiekty. Wybór sposobu odcięcia określamy podając w procentach długość wiązania, przy którym nastąpi cięcie, gdzie 100% stanowi długość ostatniego i jednocześnie najdłuższego wiązania w dendogramie.
Okno z ustawieniami opcji hierarchicznej analizy skupień wywołujemy poprzez menu Statystyki zaawansowane→Grupowanie i Redukcja→Hierarchiczna analiza skupień.
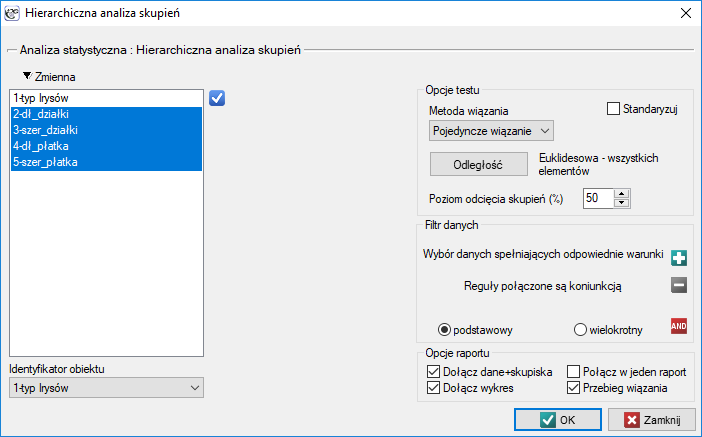
Przykład c.d. (plik iris.pqs)
Analiza przeprowadzona zostanie na klasycznym zestawie danych, dotyczącym podziału kwiatów irysa na 3 odmiany na podstawie szerokości oraz długości płatków i działek kielicha (R.A. Fishera 19361)). Ponieważ w tym zestawie danych znajduje się informacja o rzeczywistej odmianie każdego kwiatu, po przeprowadzonej analizie skupień istnieje możliwość określenia dokładności dokonanego podziału.
Przydziału kwiatów do poszczególnych grup dokonujemy na podstawie kolumn od 2 do 5. Wybieramy sposób wyliczania odległości np. odległość Euklidesową i metodę wiązania np. średnią. Podanie poziomu odcięcia skupień pozwoli na takie odcięcie dendogramu by powstały skupienia - w przypadku tej analizy chcemy uzyskać 3 skupienia i by to osiągnąć zmieniamy poziom odcięcia na 45%. Do raportu dołączamy również dane+skupienia.

Na wykresie typu dendogram, przedstawiono kolejność wiązań i ich długość.
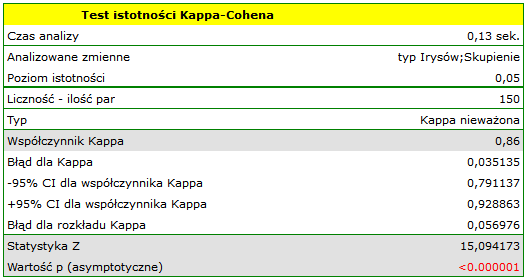
By zbadać czy wyodrębnione skupienia stanowią 3 rzeczywiste odmiany kwiatów irysa, możemy skopiować kolumnę zawierającą informację o przynależności do skupienia z raportu i wkleić do arkusza danych. Podobnie jak skupienia, odmiany opisane są również liczbowo poprzez Kody/Etykiety/Format, dlatego z łatwością można przeprowadzić analizę zgodności. Zgodność naszych wyników z rzeczywistą przynależnością danego kwiatu do odpowiedniego gatunku sprawdzimy metodą Kappa Cohena.
Dla przedstawionego przykładu obserwowaną zgodność przedstawia tabela:
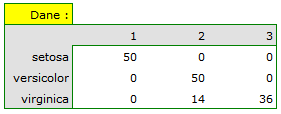
Wnioskujemy z niej, że odmiana virginica może być mylona z versicolor, dlatego obserwujemy tu 14 błędnych zaklasyfikowań. Natomiast współczynnik zgodności Kappa jest istotny statystycznie i wynosi 0.86, co świadczy o dużej zgodności uzyskanych skupień z rzeczywistą odmianą kwiatów.
1)
Fisher R.A. (1936), The use of multiple measurements in taxonomic problems. Annals of Eugenics 7 (2): 179–188
pl/statpqpl/redpl/skupienpl/hierarchpl.txt · ostatnio zmienione: 2018/02/01 17:06 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

