Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
pl:przestrzenpl:mwagpl:grpl
Macierz wag według wspólnej granicy
Do wyznaczenia macierzy wag bazującej na przyległości obiektów (wspólnej granicy), powinniśmy dysponować danymi mapy zawierającej obiekty typu wielopunkt lub wielokąt.
Kryterium wspólnej granicy
Wspólna granica porównywanych obiektów zwyczajowo rozumiana jest jako wspólny odcinek o niezerowej długości (tzn. odcinek dłuższy niż 1 punkt) – jest to sąsiedztwo typu Rook, lub jako dowolny odcinek (również o zerowej długości, czyli punkt) – jest to sąsiedztwo typu Queen.
Rodzaje macierzy wag bazujących na wspólnej granicy:
- Macierz bezpośredniego sąsiedztwa – to symetryczna macierz kwadratowa, w której na głównej przekątnej znajdują się zera, elementy poza przekątną to:
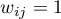 -– jeśli obiekty łączy wspólna granica,
-– jeśli obiekty łączy wspólna granica,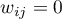 –- w przeciwnym przypadku.
–- w przeciwnym przypadku.
- Macierz sąsiedztwa (do k-tego stopnia) –- to symetryczna macierz kwadratowa, w której na głównej przekątnej znajdują się zera, elementy poza przekątną to:
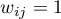 –- jeśli obiekty są bezpośrednimi sąsiadami (łączy je wspólna granica),
–- jeśli obiekty są bezpośrednimi sąsiadami (łączy je wspólna granica),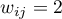 –- jeśli obiekty są sąsiadami drugiego stopnia (druga warstwa sąsiedztwa czyli tzw. sąsiad sąsiada)
–- jeśli obiekty są sąsiadami drugiego stopnia (druga warstwa sąsiedztwa czyli tzw. sąsiad sąsiada)- …
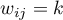 –- jeśli obiekty są sąsiadami
–- jeśli obiekty są sąsiadami  -tego stopnia (
-tego stopnia ( -ta warstwa sąsiedztwa)
-ta warstwa sąsiedztwa)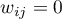 –- sąsiedztwo jest dalsze niż
–- sąsiedztwo jest dalsze niż  -tego stopnia.
-tego stopnia.
- Macierz sąsiedztwa (k-tego stopnia) –- to symetryczna macierz kwadratowa, w której na głównej przekątnej znajdują się zera, elementy poza przekątną to:
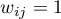 –- jeśli obiekty są sąsiadami
–- jeśli obiekty są sąsiadami  -tego stopnia (
-tego stopnia ( -ta warstwa sąsiedztwa)
-ta warstwa sąsiedztwa)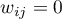 –- w przeciwnym przypadku.
–- w przeciwnym przypadku.
Macierze wag mogą być standaryzowane rzędami do jedynki – jest to zalecenie niektórych analiz statystycznych bazujących na tych macierzach.
pl/przestrzenpl/mwagpl/grpl.txt · ostatnio zmienione: 2022/02/16 12:25 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

