PQStat - Baza Wiedzy

For creating a weights matrix based on proximity of objects (contiguity) we should have at our disposal data from a map which contains objects such as a multipoint or a polygon.

Type of contiguity

The contiguity is usually understood as a common section with a non-zero length (i.e. a section longer than 1 point) – it is the Rook type neighborhood, or as any section (also of zero length, i.e. a point) – it is the Queen type neighborhood.

Weights matrix according to contiguity:

• Direct neighbors – it is a square symmetrical matrix in which on the main diagonal there are zeros, the elements outside the diagonal are:
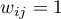  • -– if the objects are connected along a common border,
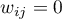  • -– in the opposite case.
• Neighbors (order of contiguity ⇐k) -– it is a square symmetrical matrix in which on the main diagonal there are zeros, the elements outside the diagonal are:
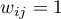  • -– if the objects are direct neighbors (they are connected along a common border),
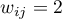  • -– if the objects are the second nearest neighbors (the second degree of neighborhood, i.e. the so-called neighbor's neighbor)
  • …
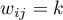  • -– if the objects are the 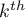neighbors ( 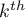degree of neighborhood)
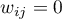  • -– neighborhood is farther than the 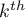degree.
• Neighbors (order of contiguity =k) -– it is a square symmetrical matrix in which on the main diagonal there are zeros, the elements outside the diagonal are:
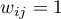  • -– if the objects are the 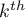neighbors ( 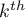degree of neighborhood)
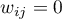  • -– in the opposite case.

Weights matrices can be row standardized -– it is the recommendation of some statistical analyses based on those matrices.