Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat Knowledge Base » PQStat - Statistic » Comparison - more than two groups
Pasek boczny
en:statpqpl:porown3grpl
Spis treści
Comparison - more than two groups
{\ovalnode{A}{\hyperlink{rozklad_normalny}{\begin{tabular}{c}Are\\the data\\normally\\distributed?\end{tabular}}}}
\rput[tl](0.15,10){\ovalnode{B}{\hyperlink{zalezne_niezalezne}{\begin{tabular}{c}Are the data\\dependent?\end{tabular}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{A}{B}
\rput[tl](4.5,9.8){\ovalnode{M}{\hyperlink{sferycznosc}{\begin{tabular}{c}Whether\\sphericity\\met?\end{tabular}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{B}{M}
\rput[br](10.9,8){\rnode{P}{\psframebox{\hyperlink{anova_repeated}{\begin{tabular}{c}ANOVA for\\dependent\\groups\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{M}{P}
\rput[br](7.7,5.5){\rnode{R}{\psframebox{\hyperlink{kor_br_sf}{\begin{tabular}{c}MANOVA\\or ANOVA\\with correction\\Epsilon, GG, H-F\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{M}{R}
\rput[tl](0.1,8){\ovalnode{C}{\hyperlink{wariancja}{\begin{tabular}{c}Are\\the variances\\equal?\end{tabular}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{B}{C}
\rput[br](3,3){\rnode{D}{\psframebox{\hyperlink{anova_one_way}{\begin{tabular}{c}ANOVA for\\independent\\groups\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{C}{D}
\rput[br](7.75,3.4){\rnode{N}{\psframebox{\hyperlink{anova_one_way_cor}{\begin{tabular}{c}ANOVA for \\independent\\groups with\\ correction $F^*$ and $F''$\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{C}{N}
\psline{->}(3.1,12.3)(6,12.3)
\rput(2.2,10.4){Y}
\rput(2.2,8.3){N}
\rput(2.2,5.3){Y}
\rput(4.8,12.5){N}
\rput(6.8,11.4){Y}
\rput(8.9,11.4){N}
\rput(11.9,11.4){Y}
\rput(14.1,11.4){N}
\rput(4.2,9.5){Y}
\rput(4.1,6.1){N}
\rput(8.5,9.1){Y}
\rput(6.5,7.7){N}
\rput(8,14){Ordinal scale}
\rput[tl](6,13){\ovalnode{E}{\hyperlink{zalezne_niezalezne}{\begin{tabular}{c}Are the data\\dependent?\end{tabular}}}}
\rput[br](7.8,10){\rnode{F}{\psframebox{\hyperlink{anova_friedmana}{\begin{tabular}{c}Friedman\\ANOVA\end{tabular}}}}}
\rput[br](10.0,9.6){\rnode{G}{\psframebox{\hyperlink{anova_kruskal-wallis}{\begin{tabular}{c}Kruskal\\Wallis\\ANOVA\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{E}{F}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{E}{G}
\rput(13,14){Nominal scale}
\rput[tl](11,13){\ovalnode{H}{\hyperlink{zalezne_niezalezne}{\begin{tabular}{c}Are the data\\dependent?\end{tabular}}}}
\rput[br](13.1,10){\rnode{I}{\psframebox{\hyperlink{anova_q_cochrana}{\begin{tabular}{c}Q-Cochran\\ANOVA\end{tabular}}}}}
\rput[br](16.1,8.41){\rnode{J}{\psframebox{\hyperlink{chi_kwadrat_olbrzymi}{\begin{tabular}{c}multidimentional\\$\chi^2$ test\end{tabular}}}}}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{H}{I}
\ncline[angleA=-90, angleB=90, arm=.5, linearc=.2]{->}{H}{J}
\rput(3.5,4.9){\hyperlink{test_levenea}{Levenea,}}
\rput(3.1,4.6){\hyperlink{test_levenea}{Brown-Forsythe}}
\psline[linestyle=dotted]{<-}(2.6,6.2)(3.5,5.0)
\rput(4,10.8){\hyperlink{testy_normalnosci}{normality tests}}
\psline[linestyle=dotted]{<-}(3.2,11.4)(3.9,11.2)
\rput(9.0,7.0){\hyperlink{sferycznosc}{Mauchly test}}
\psline[linestyle=dotted]{<-}(7.9,8.1)(9.0,7.3)
\end{pspicture}](/lib/plugins/latex/images/renderfail.png)
Note
The proposed test selection scheme for the multiple group comparison is not the only possible scheme and does not include all the tests proposed in the software for this comparison.
Note
Note, that simultaneous comparison of more than two groups can NOT be replaced with multiple performance the tests for the comparison of two groups. It is the result of the necessity of controlling the I type error  . Choosing the
. Choosing the  and using the
and using the  -fold selected test for the comparison of 2 groups, we could make the assumed level much higher
-fold selected test for the comparison of 2 groups, we could make the assumed level much higher  . It is possible to avoid this error using the ANOVA test (Analysis of Variance) and contrasts or the POST-HOC tests dedicated to them.
. It is possible to avoid this error using the ANOVA test (Analysis of Variance) and contrasts or the POST-HOC tests dedicated to them.
Parametric tests
The ANOVA for independent groups
The one-way analysis of variance (ANOVA for independent groups) proposed by Ronald Fisher, is used to verify the hypothesis determining the equality of means of an analysed variable in several (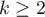 ) populations.
) populations.
Basic assumptions:
- measurement on an interval scale,
- normality of distribution of an analysed feature in each population,
- equality of variances of an analysed variable in all populations.
Hypotheses:
where:
 ,
, ,…,
,…,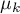 – means of an analysed variable of each population.
– means of an analysed variable of each population.
The test statistic is defined by:
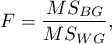
where:
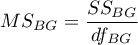 – mean square between-groups,
– mean square between-groups,
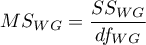 – mean square within-groups,
– mean square within-groups,
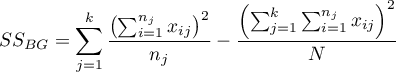 – between-groups sum of squares,
– between-groups sum of squares,
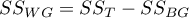 – within-groups sum of squares,
– within-groups sum of squares,
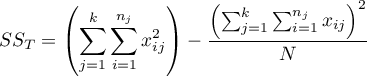 – total sum of squares,
– total sum of squares,
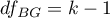 – between-groups degrees of freedom,
– between-groups degrees of freedom,
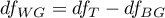 – within-groups degrees of freedom,
– within-groups degrees of freedom,
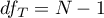 – total degrees of freedom,
– total degrees of freedom,
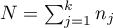 ,
,
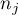 – samples sizes for
– samples sizes for  ,
,
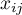 – values of a variable taken from a sample for
– values of a variable taken from a sample for 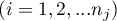 ,
,  .
.
The F statistic has the F Snedecor distribution with 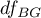 and
and 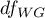 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Effect size - partial 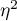
This quantity indicates the proportion of explained variance to total variance associated with a factor. Thus, in a one-factor ANOVA model for independent groups, it indicates what proportion of the between-groups variability in outcomes can be attributed to the factor under study determining the independent groups.
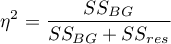
POST-HOC tests
Introduction to contrast and POST-HOC testing
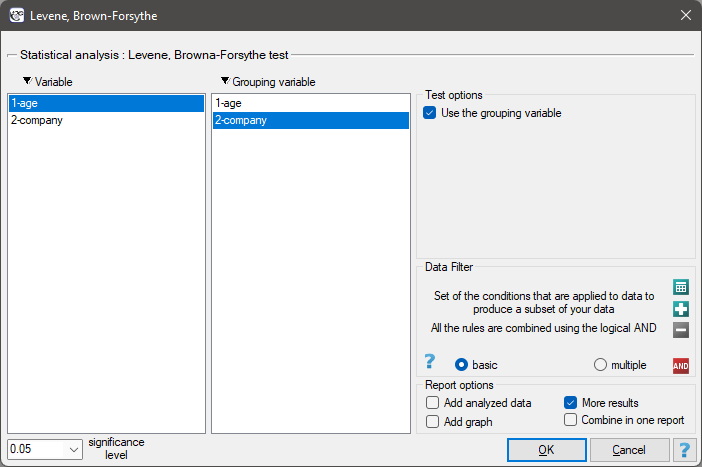
The settings window with the One-way ANOVA for independent groups can be opened in Statistics menu→Parametric tests→ANOVA for independent groups or in ''Wizard''.
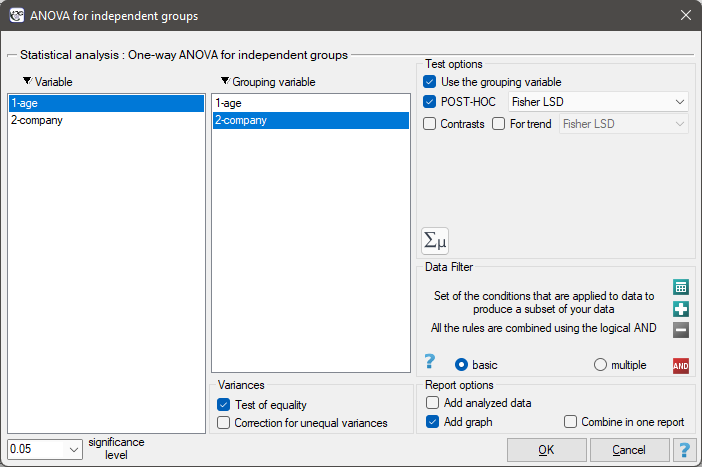
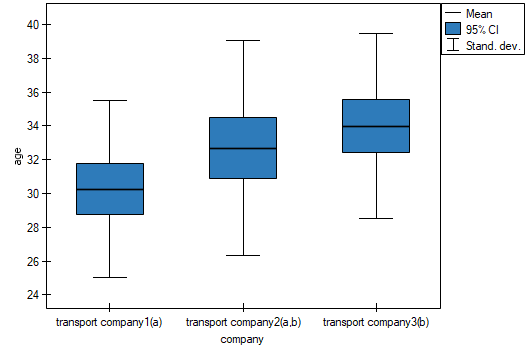
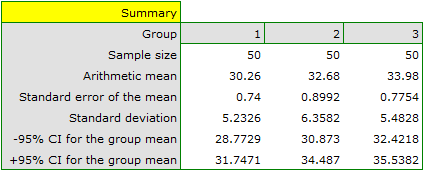
There are 150 persons chosen randomly from the population of workers of 3 different transport companies. From each company there are 50 persons drawn to the sample. Before the experiment begins, you should check if the average age of the workers of these companies is similar, because the next step of the experiment depends on it. The age of each participant is written in years.
Age (company 1): 27, 33, 25, 32, 34, 38, 31, 34, 20, 30, 30, 27, 34, 32, 33, 25, 40, 35, 29, 20, 18, 28, 26, 22, 24, 24, 25, 28, 32, 32, 33, 32, 34, 27, 34, 27, 35, 28, 35, 34, 28, 29, 38, 26, 36, 31, 25, 35, 41, 37\\Age (company 2): 38, 34, 33, 27, 36, 20, 37, 40, 27, 26, 40, 44, 36, 32, 26, 34, 27, 31, 36, 36, 25, 40, 27, 30, 36, 29, 32, 41, 49, 24, 36, 38, 18, 33, 30, 28, 27, 26, 42, 34, 24, 32, 36, 30, 37, 34, 33, 30, 44, 29\\Age (company 3): 34, 36, 31, 37, 45, 39, 36, 34, 39, 27, 35, 33, 36, 28, 38, 25, 29, 26, 45, 28, 27, 32, 33, 30, 39, 40, 36, 33, 28, 32, 36, 39, 32, 39, 37, 35, 44, 34, 21, 42, 40, 32, 30, 23, 32, 34, 27, 39, 37, 35.
Before proceeding with the ANOVA analysis, the normality of the data distribution was confirmed.
The analysis window tested the assumption of equality of variance, obtaining p>0.05 in both tests.
Hypotheses:
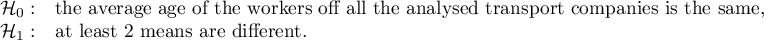
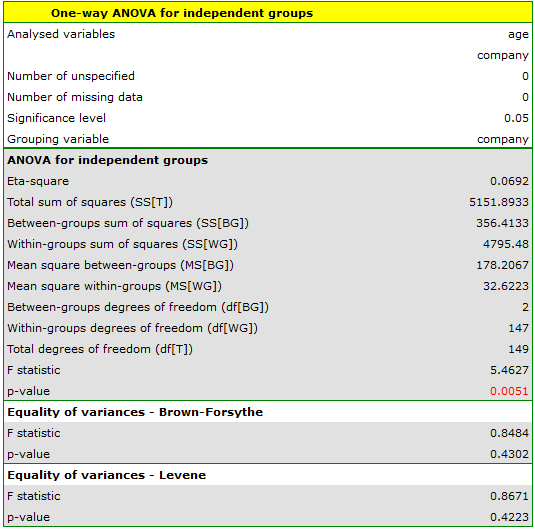
Comparing the p-value = 0.005147 of the one-way analysis of variance with the significance level  , you can draw the conclusion that the average ages of workers of these transport companies is not the same. Based just on the ANOVA result, you do not know precisely which groups differ from others in terms of age. To gain such knowledge, it must be used one of the POST-HOC tests, for example the Tukey test. To do this, you should resume the analysis by clicking
, you can draw the conclusion that the average ages of workers of these transport companies is not the same. Based just on the ANOVA result, you do not know precisely which groups differ from others in terms of age. To gain such knowledge, it must be used one of the POST-HOC tests, for example the Tukey test. To do this, you should resume the analysis by clicking  and then, in the options window for the test, you should select
and then, in the options window for the test, you should select Tukey HSD and Add graph.
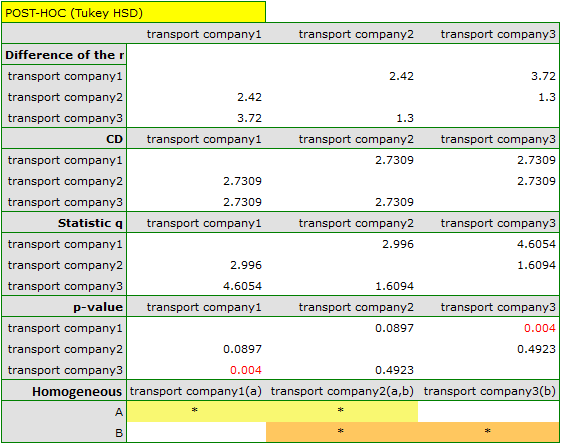
The critical difference (CD) calculated for each pair of comparisons is the same (because the groups sizes are equal) and counts to 2.730855. The comparison of the 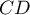 value with the value of the mean difference indicates, that there are significant differences only between the mean age of the workers from the first and the third transport company (only if these 2 groups are compared, the
value with the value of the mean difference indicates, that there are significant differences only between the mean age of the workers from the first and the third transport company (only if these 2 groups are compared, the 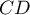 value is less than the difference of the means). The same conclusion you draw, if you compare the p-value of POST-HOC test with the significance level
value is less than the difference of the means). The same conclusion you draw, if you compare the p-value of POST-HOC test with the significance level  . The workers of the first transport company are about 3 years younger (on average) than the workers of the third transport company. Two interlocking homogeneous groups were obtained, which are also marked on the graph.
. The workers of the first transport company are about 3 years younger (on average) than the workers of the third transport company. Two interlocking homogeneous groups were obtained, which are also marked on the graph.
We can provide a detailed description of the data by selecting Descriptive statistics in the analysis window 
2022/02/09 12:56
The contrasts and the POST-HOC tests
An analysis of the variance enables you to get information only if there are any significant differences among populations. It does not inform you which populations are different from each other. To gain some more detailed knowledge about the differences in particular parts of our complex structure, you should use contrasts (if you do the earlier planned and usually only particular comparisons), or the procedures of multiple comparisons POST-HOC tests (when having done the analysis of variance, we look for differences, usually between all the pairs).
The number of all the possible simple comparisons is calculated using the following formula:
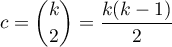
Hypotheses:
The first example - simple comparisons (comparison of 2 selected means):
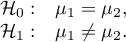
The second example - complex comparisons (comparison of combination of selected means):
![LaTeX \begin{array}{cc}
\mathcal{H}_0: & \mu_1=\frac{\mu_2+\mu_3}{2},\\[0.1cm]
\mathcal{H}_1: & \mu_1\neq\frac{\mu_2+\mu_3}{2}.
\end{array}](/lib/exe/fetch.php?media=wiki:latex:/imgf0472a7ad15f9b99bbf5ce50cb721339.png)
If you want to define the selected hypothesis you should ascribe the contrast value 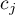 ,
,  to each mean. The
to each mean. The 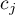 values are selected, so that their sums of compared sides are the opposite numbers, and their values of means which are not analysed count to 0.
values are selected, so that their sums of compared sides are the opposite numbers, and their values of means which are not analysed count to 0.
- The first example:
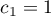 ,
,  ,
, 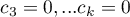 .
. - The second example:
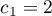 ,
,  ,
, 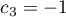 ,
, 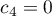 ,…,
,…, 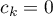 .
.
How to choose the proper hypothesis:
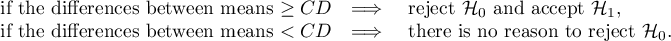
- [ii] The p-value, designated on the basis of the proper POST-HOC test, is compared with the significance level
 :
:

For simple and complex comparisons, equal-size groups as well as unequal-size groups, when the variances are equal.
- [i] The value of critical difference is calculated by using the following formula:
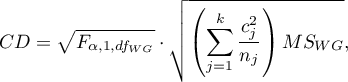
where:
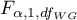 - is the critical value (statistic) of the F Snedecor distribution for a given significance level
- is the critical value (statistic) of the F Snedecor distribution for a given significance level and degrees of freedom, adequately: 1 and
and degrees of freedom, adequately: 1 and 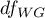 .
.
- [ii] The test statistic is defined by:
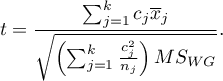
The test statistic has the t-student distribution with 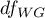 degrees of freedom.
degrees of freedom.
For simple comparisons, equal-size groups as well as unequal-size groups, when the variances are equal.
- [i] The value of a critical difference is calculated by using the following formula:
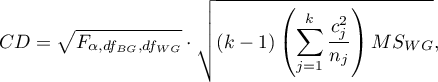
where:
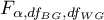 - is the critical value(statistic) of the F Snedecor distribution for a given significance level
- is the critical value(statistic) of the F Snedecor distribution for a given significance level  and
and 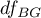 and
and 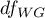 degrees of freedom.
degrees of freedom.
- [ii] The test statistic is defined by:
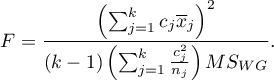
The test statistic has the F Snedecor distribution with 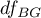 and
and 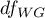 degrees of freedom.
degrees of freedom.
For simple comparisons, equal-size groups as well as unequal-size groups, when the variances are equal.
- [i] The value of a critical difference is calculated by using the following formula:
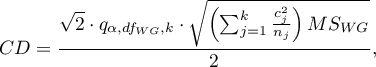
where:
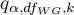 - is the critical value (statistic) of the studentized range distribution for a given significance level
- is the critical value (statistic) of the studentized range distribution for a given significance level and
and 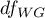 and
and  degrees of freedom.
degrees of freedom.
- [ii] The test statistic is defined by:
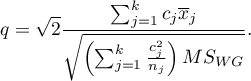
The test statistic has the studentized range distribution with 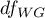 and
and  degrees of freedom.
Info.
degrees of freedom.
Info.
The algorithm for calculating the p-value and the statistic of the studentized range distribution in PQStat is based on the Lund works (1983)1). Other applications or web pages may calculate a little bit different values than PQStat, because they may be based on less precised or more restrictive algorithms (Copenhaver and Holland (1988), Gleason (1999)).
The test examining the existence of a trend can be calculated in the same situation as ANOVA for independent variables, because it is based on the same assumptions, but it captures the alternative hypothesis differently - indicating in it the existence of a trend in the mean values for successive populations. The analysis of the trend in the arrangement of means is based on contrasts Fisher LSD. By building appropriate contrasts, you can study any type of trend such as linear, quadratic, cubic, etc. Below is a table of sample contrast values for selected trends.
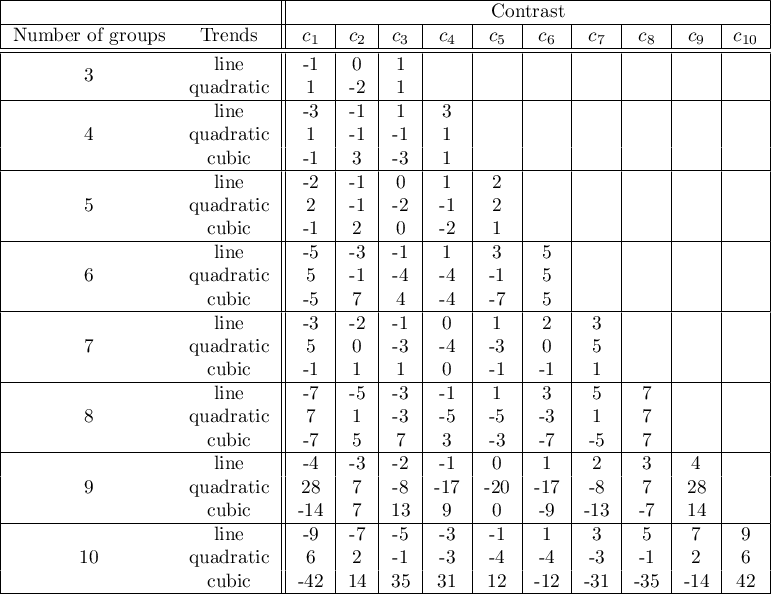
Linear trend
A linear trend, like other trends, can be analyzed by entering the appropriate contrast values. However, if the direction of the linear trend is known, simply use the For trend option and indicate the expected order of the populations by assigning them consecutive natural numbers.
The analysis is performed on the basis of linear contrast, i.e. the groups indicated according to the natural order are assigned appropriate contrast values and the statistics are calculated Fisher LSD .
With the expected direction of the trend known, the alternative hypothesis is one-sided and the one-sided  -value is interpreted. The interpretation of the two-sided
-value is interpreted. The interpretation of the two-sided  -value means that the researcher does not know (does not assume) the direction of the possible trend.
-value means that the researcher does not know (does not assume) the direction of the possible trend.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

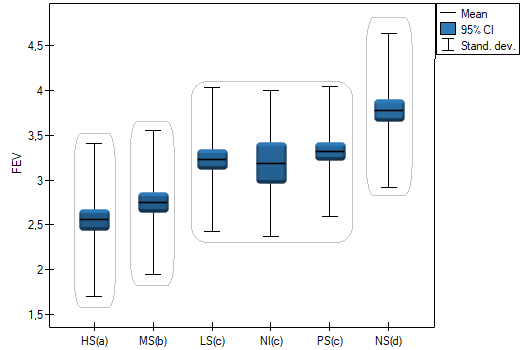
For each post-hoc test, homogeneous groups are constructed. Each homogeneous group represents a set of groups that are not statistically significantly different from each other. For example, suppose we divided subjects into six groups regarding smoking status: Nonsmokers (NS), Passive smokers (PS), Noninhaling smokers (NI), Light smokers (LS), Moderate smokers (MS), Heavy smokers (HS) and we examine the expiratory parameters for them. In our ANOVA we obtained statistically significant differences in exhalation parameters between the tested groups. In order to indicate which groups differ significantly and which do not, we perform post-hoc tests. As a result, in addition to the table with the results of each pair of comparisons and statistical significance in the form of  :
:
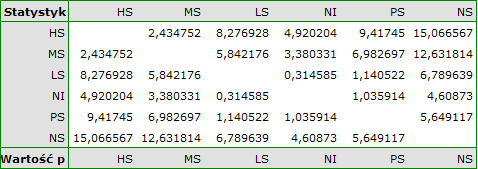
we obtain a division into homogeneous groups:
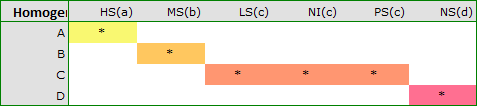
In this case we obtained 4 homogeneous groups, i.e. A, B, C and D, which indicates the possibility of conducting the study on the basis of a smaller division, i.e. instead of the six groups we studied originally, further analyses can be conducted on the basis of the four homogeneous groups determined here. The order of groups was determined on the basis of weighted averages calculated for particular homogeneous groups in such a way, that letter A was assigned to the group with the lowest weighted average, and further letters of the alphabet to groups with increasingly higher averages.
The settings window with the One-way ANOVA for independent groups can be opened in Statistics menu→Parametric tests→ANOVA for independent groups or in ''Wizard''.

2022/02/09 12:56
The ANOVA for independent groups with F* and F" corrections
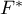 (Brown-Forsythe, 19742)) and
(Brown-Forsythe, 19742)) and 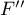 (Welch, 19513)) Corrections concern ANOVA for independent groups and are calculated when the assumption of equality of variances is not met.
(Welch, 19513)) Corrections concern ANOVA for independent groups and are calculated when the assumption of equality of variances is not met.
The test statistic is in the form of:
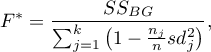
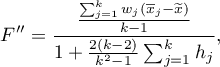
where:
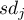 – group standard deviation
– group standard deviation  ,
,
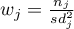 – group weight
– group weight  ,
,
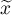 – weighted mean,
– weighted mean,
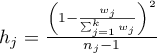 .
.
This statistic is subject toSnedecor's F distribution with 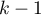 and adjusted
and adjusted 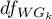 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

POST-HOC Tests
Introduction to the contrasts and POST-HOC tests was done in chapter concerning one-way analysis of variance.
For simple and complex comparisons, equal-size groups as well as unequal-size groups, when the variances differ significantly (Tamhane A. C., 19774)).
- [i] The value of critical difference is calculated by using the following formula:
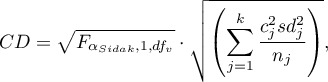
where:
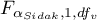 - is the critical value (statistics) of the Snedecor's F distribution for modified significance level
- is the critical value (statistics) of the Snedecor's F distribution for modified significance level 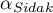 and for degrees of freedom 1 and
and for degrees of freedom 1 and 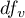 respectively,
respectively,
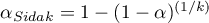 ,
,
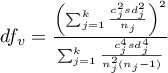
- [ii] The test statistic is in the form of:
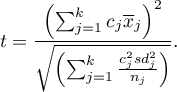
This statistic is subject to the t-Student distribution with 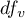 degrees of freedom, and p-value is adjusted by the number of possible simple comparisons.
degrees of freedom, and p-value is adjusted by the number of possible simple comparisons.
BF test (Brown-Forsythe)
For simple and complex comparisons, equal-size groups as well as unequal-size groups, when the variances differ significantly (Brown M. B. i Forsythe A. B. (1974)5)).
- [i] The value of critical difference is calculated by using the following formula:
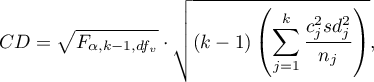
where:
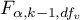 - is the critical value (statistics) of the Snedecor's F distribution for a given significance level
- is the critical value (statistics) of the Snedecor's F distribution for a given significance level as well as
as well as 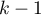 and
and 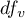 degrees of freedom.
degrees of freedom.
- [ii] The test statistic is in the form of:
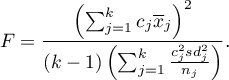 This statistic is subject to Snedecor's F distribution with
This statistic is subject to Snedecor's F distribution with 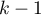 and
and 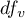 degrees of freedom.
degrees of freedom.
GH test (Games-Howell).
For simple and complex comparisons, equal-size groups as well as unequal-size groups, when the variances differ significantly (Games P. A. i Howell J. F. 19766)).
- [i] The value of critical difference is calculated by using the following formula:
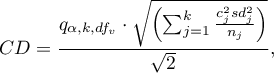
gdzie:
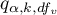 - is the critical value (statistics) of the the distribution of the studentised interval for a given significance level
- is the critical value (statistics) of the the distribution of the studentised interval for a given significance level  as well as
as well as  and
and 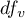 degrees of freedom.
degrees of freedom.
- [ii] The test statistic is in the form of:
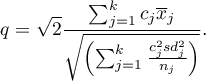 This statistic follows a studenty distribution with
This statistic follows a studenty distribution with  and
and 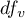 degrees of freedom.
degrees of freedom.
Trend test.
The test examining the presence of a trend can be calculated in the same situation as ANOVA for independent groups with correction 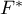 and
and 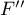 , because it is based on the same assumptions, however, differently captures the alternative hypothesis - indicating the existence of a trend in the mean values for successive populations. The analysis of the trend of the arrangement of means is based on contrasts (T2 Tamhane). By creating appropriate contrasts you can study any type of trend e.g. linear, quadratic, cubic, etc. A table of sample contrast values for certain trends can be found in the description trend test for Ona-Way ANOVA.
, because it is based on the same assumptions, however, differently captures the alternative hypothesis - indicating the existence of a trend in the mean values for successive populations. The analysis of the trend of the arrangement of means is based on contrasts (T2 Tamhane). By creating appropriate contrasts you can study any type of trend e.g. linear, quadratic, cubic, etc. A table of sample contrast values for certain trends can be found in the description trend test for Ona-Way ANOVA.
Linear trend
A linear trend, like other trends, can be analyzed by entering the appropriate contrast values. However, if the direction of the linear trend is known, simply use the Linear Trend option and indicate the expected order of the populations by assigning them consecutive natural numbers.
The analysis is performed based on linear contrast, i.e., the groups indicated according to the natural ordering are assigned appropriate contrast values and the T2 Tamhane statistic is calculated.
With the expected direction of the trend being known, the alternative hypothesis is one-sided and the one-sided value of  is subject to interpretation. The interpretation of the two-sided value of
is subject to interpretation. The interpretation of the two-sided value of  means that the researcher does not know (does not assume) the direction of the possible trend.
means that the researcher does not know (does not assume) the direction of the possible trend.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Settings window for the One-way ANOVA for independent groups with F* and F„ adjustments is opened via menu Statistics→Parametric tests→ANOVA for independent groups or via the ''Wizard''.
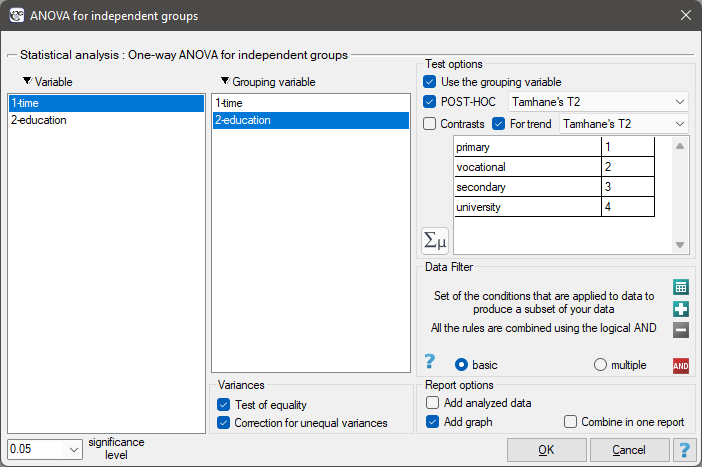
EXAMPLE (unemployment.pqs file)
There are many factors that control the time it takes to find a job during an economic crisis. One of the most important may be the level of education. Sample data on education and time (in months) of unemployment are gathered in the file. We want to see if there are differences in average job search time for different education categories.
Hypotheses:
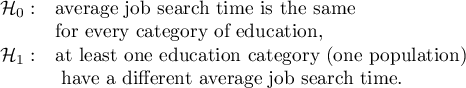
Due to differences in variance between populations (for Levene test 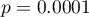 and for Brown-Forsythe test
and for Brown-Forsythe test 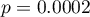 ):
):

the analysis is performed with the correction of various variances enabled. The obtained result of the adjusted 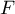 statistic is shown below.
statistic is shown below.
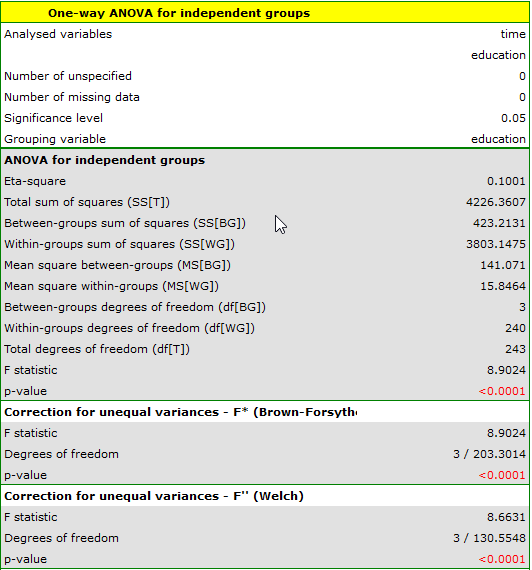
Comparing 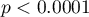 (for the
(for the 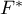 test) and
test) and 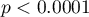 (for the
(for the 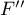 test) with a significance level of
test) with a significance level of  , we find that the average job search time differs depending on the education one has. By performing one of the POST-HOC tests, designed to compare groups with different variances, we find out which education categories are affected by the differences found:
, we find that the average job search time differs depending on the education one has. By performing one of the POST-HOC tests, designed to compare groups with different variances, we find out which education categories are affected by the differences found:
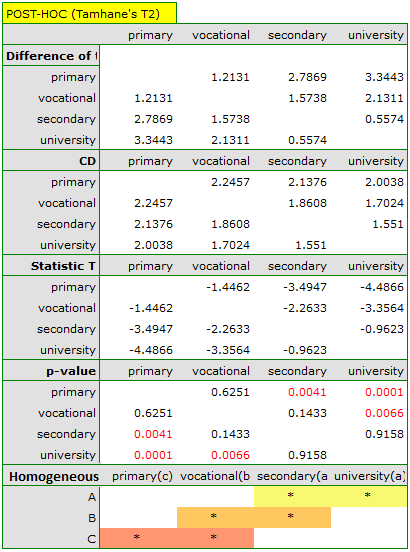
The least significant difference (LSD) determined for each pair of comparisons is not the same (even though the group sizes are equal) because the variances are not equal. Relating the LSD value to the resulting differences in mean values yields the same result as comparing the p-value with a significance level of  . The differences are between primary and higher education, primary and secondary education, and vocational and higher education. The resulting homogeneous groups overlap. In general, however, looking at the graph, we might expect that the more educated a person is, the less time it takes them to find a job.
. The differences are between primary and higher education, primary and secondary education, and vocational and higher education. The resulting homogeneous groups overlap. In general, however, looking at the graph, we might expect that the more educated a person is, the less time it takes them to find a job.
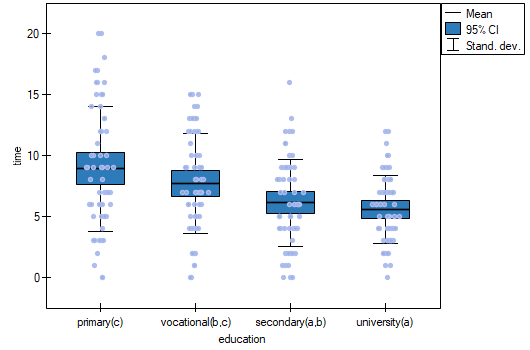
In order to test the stated hypothesis, it is necessary to perform the trend analysis. To do so, we {reopen the analysis} with the  button and, in the test options window, select: the
button and, in the test options window, select: the Tamhane's T2 method, the Contrasts option (and set the appropriate contrast), or the For trend option (and indicate the order of education categories by specifying consecutive natural numbers).
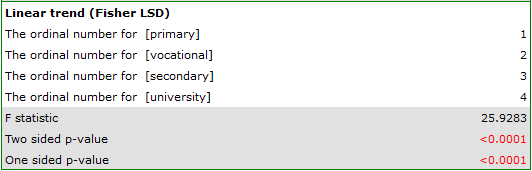
Depending on whether the direction of the correlation between education and job search time is known to us, we use a one-sided or two-sided p-value. Both of these values are less than the given significance level. The trend we predicted is confirmed, that is, at a significance level of  we can say that this trend does indeed exist in the population from which the sample is drawn.
we can say that this trend does indeed exist in the population from which the sample is drawn.
2022/02/09 12:56
The Brown-Forsythe test and the Levene test
Both tests: the Levene test (Levene, 1960 7)) and the Brown-Forsythe test (Brown and Forsythe, 1974 8)) are used to verify the hypothesis determining the equality of variance of an analysed variable in several (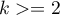 ) populations.
) populations.
Basic assumptions:
- measurement on an interval scale,
- normality of distribution of an analysed feature in each population,
Hypotheses:
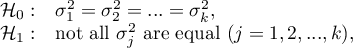
where:
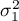 ,
,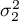 ,…,
,…,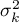
 variances of an analysed variable of each population.
variances of an analysed variable of each population.
The analysis is based on calculating the absolute deviation of measurement results from the mean (in the Levene test) or from the median (in the Brown-Forsythe test), in each of the analysed groups. This absolute deviation is the set of data which are under the same procedure performed to the analysis of variance for independent groups. Hence, the test statistic is defined by:
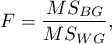
The test statistic has the F Snedecor distribution with 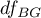 and
and 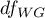 degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Note
The Brown-Forsythe test is less sensitive than the Levene test, in terms of an unfulfilled assumption relating to distribution normality.
The settings window with the Levene, Brown-Forsythe tests' can be opened in Statistics menu→Parametric tests→Levene, Brown-Forsythe.
2022/02/09 12:56
The ANOVA for dependent groups
The single-factor repeated-measures analysis of variance (ANOVA for dependent groups) is used when the measurements of an analysed variable are made several times (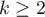 ) each time in different conditions (but we need to assume that the variances of the differences between all the pairs of measurements are pretty close to each other).
) each time in different conditions (but we need to assume that the variances of the differences between all the pairs of measurements are pretty close to each other).
This test is used to verify the hypothesis determining the equality of means of an analysed variable in several (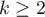 ) populations.
) populations.
Basic assumptions:
- measurement on an interval scale,
- the normal distribution for all variables which are the differences of measurement pairs (or the normal distribution for an analysed variable in each measurement),
Hypotheses:
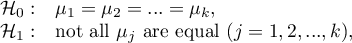
where:
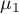 ,
,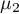 ,…,
,…,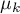 – means for an analysed features, in the following measurements from the examined population.
– means for an analysed features, in the following measurements from the examined population.
The test statistic is defined by:
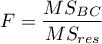
where:
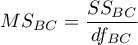 – mean square between-conditions,
– mean square between-conditions,
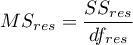 – mean square residual,
– mean square residual,
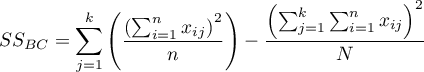 – between-conditions sum of squares,
– between-conditions sum of squares,
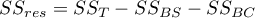 – residual sum of squares,
– residual sum of squares,
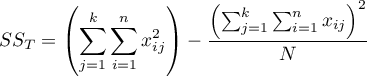 – total sum of squares,
– total sum of squares,
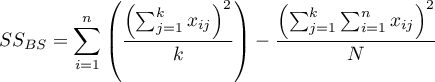 – between-subjects sum of squares,
– between-subjects sum of squares,
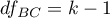 – between-conditions degrees of freedom,
– between-conditions degrees of freedom,
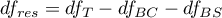 – residual degrees of freedom,
– residual degrees of freedom,
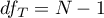 – total degrees of freedom,
– total degrees of freedom,
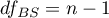 – between-subjects degrees of freedom,
– between-subjects degrees of freedom,
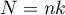 ,
,
 – sample size,
– sample size,
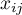 – values of the variable from
– values of the variable from  subjects
subjects 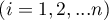 in
in  conditions
conditions  .
.
The test statistic has the F Snedecor distribution with 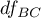 and
and 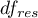 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Effect size - partial <latex>$\eta^2$</latex>
This quantity indicates the proportion of explained variance to total variance associated with a factor. Thus, in a repeated measures model, it indicates what proportion of the between-conditions variability in outcomes can be attributed to repeated measurements of the variable.
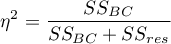
Testy POST-HOC
Introduction to the contrasts and the POST-HOC tests was performed in the \ref{post_hoc} unit, which relates to the one-way analysis of variance.
For simple and complex comparisons (frequency in particular measurements is always the same).
Hypotheses:
Example - simple comparisons (comparison of 2 selected means):
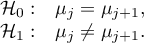
- [i] The value of the critical difference is calculated by using the following formula:
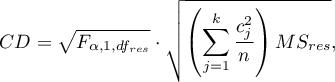
where:
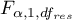 - is the critical value (statistic) of the F Snedecor distribution for a given significance level
- is the critical value (statistic) of the F Snedecor distribution for a given significance level  and degrees of freedom, adequately: 1 and
and degrees of freedom, adequately: 1 and 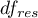 .
.
- [ii] The test statistic is defined by:
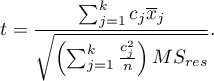
The test statistic has the t-Student distribution with 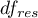 degrees of freedom.
Note!
degrees of freedom.
Note!
For contrasts 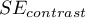 is used instead of
is used instead of 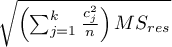 , and degrees of freedem:
, and degrees of freedem: 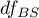 .
.
For simple comparisons (frequency in particular measurements is always the same).
- [i] The value of the critical difference is calculated by using the following formula:

where:
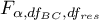 - is the critical value (statistic) of the F Snedecor distribution for a given significance level
- is the critical value (statistic) of the F Snedecor distribution for a given significance level  and
and 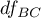 and
and 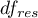 degrees of freedom.
degrees of freedom.
- [
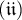 ] The test statistic is defined by:
] The test statistic is defined by:
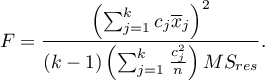 The test statistic has the F Snedecor distribution with
The test statistic has the F Snedecor distribution with 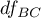 and
and 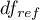 degrees of freedom.
degrees of freedom.
For simple comparisons (frequency in particular measurements is always the same).
- [i] The value of the critical difference is calculated by using the following formula:
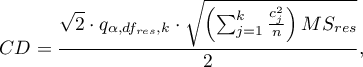
where:
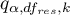 - is the critical value (statistic) of the studentized range distribution for a given significance level
- is the critical value (statistic) of the studentized range distribution for a given significance level  and
and 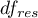 and
and  degrees of freedom.
degrees of freedom.
- [ii] The test statistic is defined by:
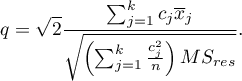
The test statistic has the studentized range distribution with 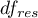 and
and  degrees of freedom.
degrees of freedom.
Info.
The algorithm for calculating the p-value and statistic of the studentized range distribution in PQStat is based on the Lund works (1983)\cite{lund}. Other applications or web pages may calculate a little bit different values than PQStat, because they may be based on less precised or more restrictive algorithms (Copenhaver and Holland (1988), Gleason (1999)).
Test for trend.
The test that examines the existence of a trend can be calculated in the same situation as ANOVA for dependent variables, because it is based on the same assumptions, but it captures the alternative hypothesis differently – indicating in it the existence of a trend of mean values in successive measurements. The analysis of the trend in the arrangement of means is based on contrasts Fisher LSD test. By building appropriate contrasts, you can study any type of trend, e.g. linear, quadratic, cubic, etc. A table of example contrast values for selected trends can be found in the description of the testu dla trendu for ANOVA of independent variables.
Linear trend
Trend liniowy, tak jak pozostałe trendy, możemy analizować wpisując odpowiednie wartości kontrastów. Jeśli jednak znany jest kierunek trendu liniowego, wystarczy skorzystać z opcji Trend liniowy i wskazać oczekiwaną kolejność populacji przypisując im kolejne liczby naturalne.
A linear trend, like other trends, can be analyzed by entering the appropriate contrast values. However, if the direction of the linear trend is known, simply use the Fisher LSD test option and indicate the expected order of the populations by assigning them consecutive natural numbers.
With the expected direction of the trend known, the alternative hypothesis is one-sided and the one-sided p-values is interpreted. The interpretation of the two-sided p-value means that the researcher does not know (does not assume) the direction of the possible trend.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The settings window with the Single-factor repeated-measures ANOVA can be opened in Statistics menu→Parametric tests→ANOVA for dependent groups or in ''Wizard''.
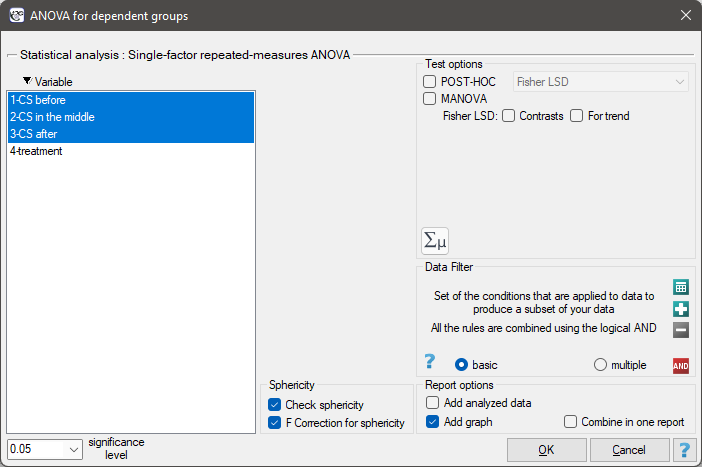
EXAMPLE (pressure.pqs file)
2022/02/09 12:56
The ANOVA for dependent groups with Epsilon correction and MANOVA
Epsilon and MANOVA corrections apply to repeated measurements ANOVA and are calculated when the assumption of sphericity is not met or the variances of the differences between all pairs of measurements are not close to each other.
Correction of non-sphericity
The degree to which sphericity is met is represented by the value of  in the Mauchly test, but also by the values of Epsilon (
in the Mauchly test, but also by the values of Epsilon (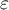 ) calculated with corrections.
) calculated with corrections. 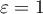 indicates strict adherence to the sphericity condition. The smaller the value of Epsilon is compared to 1, the more the sphericity assumption is affected. The lower limit that Epsilon can reach is
indicates strict adherence to the sphericity condition. The smaller the value of Epsilon is compared to 1, the more the sphericity assumption is affected. The lower limit that Epsilon can reach is 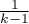 .
.
To minimize the effects of non-sphericity, three corrections can be used to change the number of degrees of freedom when testing from an F distribution. The simplest but weakest is the Epsilon lower bound correction. A slightly stronger but also conservative one is the Greenhouse-Geisser correction (1959)9). The strongest is the correction by Huynh-Feldt (1976)10). When sphericity is significantly affected, however, it is most appropriate to perform an analysis that does not require this assumption, namely MANOVA.
A multidimensional approach - MANOVA
MANOVA i.e. multivariate analysis of variance not assuming sphericity. If this assumption is not met, it is the most efficient method, so it should be chosen as a substitute for analysis of variance for repeated measurements. For a description of this method, see univariate MANOVA. Its use for repeated measures (without the independent groups factor) limits its application to data that are differences of adjacent measurements and provides testing of the same hypothesis as ANOVA for dependent variables.
Settings window for ANOVA for dependent groups with Epsilon correction and MANOVA is opened via menu Statistics→Parametric tests→ANOVA for dependent groups or via ''Wizard''.
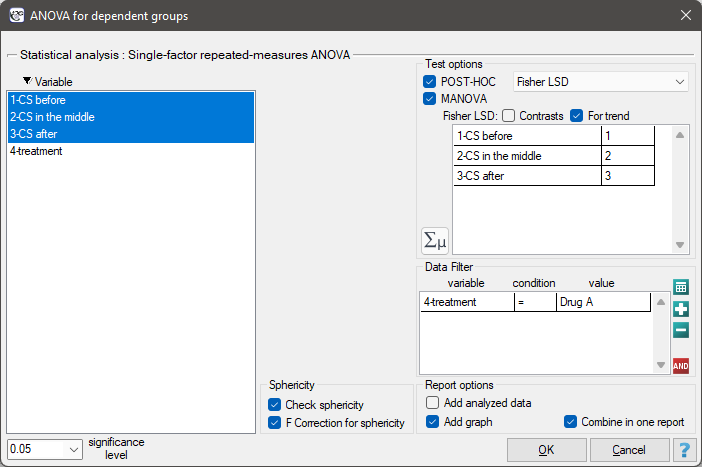
The effectiveness of two treatments for hypertension was analyzed. A sample of 56 patients was collected and randomly assigned to two groups: group treated with drug A and group treated with drug B. Systolic blood pressure was measured three times in each group: before treatment, during treatment and after 6 months of treatment.
Hypotheses for treated with drug A:

The hypotheses for those treated with drug B read similar.
Since the data have a normal distribution, we begin our analysis by testing the assumption of sphericity. We perform the testing for each group separately using a multiple filter.
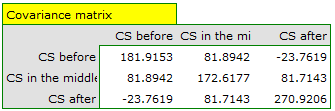
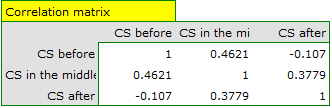
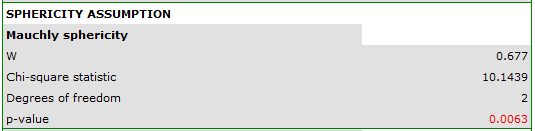
Failure to meet the sphericity assumption by the group treated with drug B is indicated by both the observed values of the covariance and correlation matrix and the result of the Mauchly test (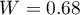 , p=0.0063.
, p=0.0063.
We resume our analysis  and in the test options window select the primary filter to perform a repeated-measures ANOVA - for those treated with drug A, followed by a correction of this analysis and a MANOVA statistic - for those treated with drug B.
and in the test options window select the primary filter to perform a repeated-measures ANOVA - for those treated with drug A, followed by a correction of this analysis and a MANOVA statistic - for those treated with drug B.
Results for those treated with drug A:
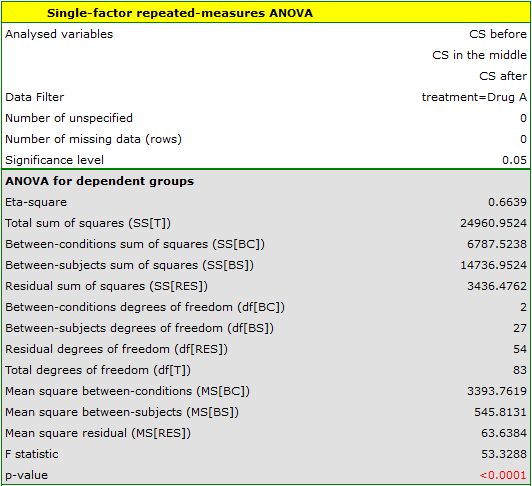
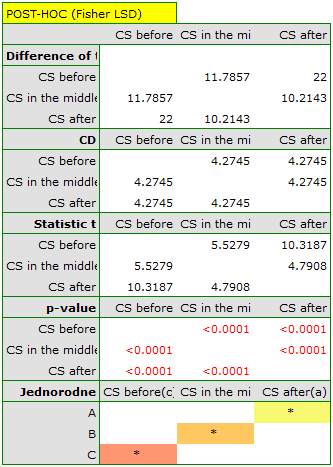
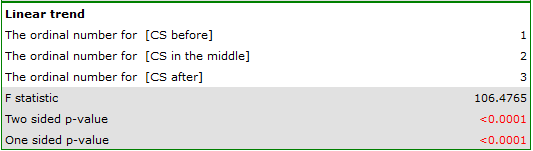
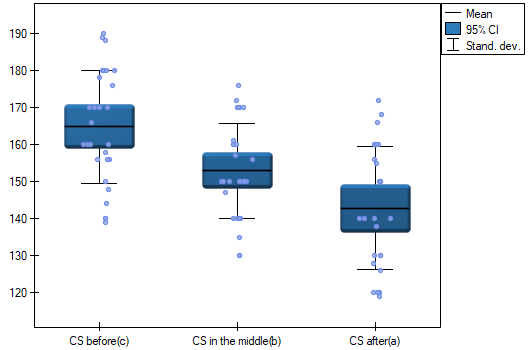
indicate significant (at the level of significance  ) differences between mean systolic blood pressure values (p<0.0001 for repeated measures ANOVA). More than 66% of the between-conditions variation in outcomes can be explained by the use of drug A (
) differences between mean systolic blood pressure values (p<0.0001 for repeated measures ANOVA). More than 66% of the between-conditions variation in outcomes can be explained by the use of drug A (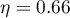 ). The differences apply to all treatment stages compared (POST-HOC score). The decrease in systolic blood pressure due to treatment is also significant (p<0.0001). Thus, we can consider Drug A as an effective drug.
). The differences apply to all treatment stages compared (POST-HOC score). The decrease in systolic blood pressure due to treatment is also significant (p<0.0001). Thus, we can consider Drug A as an effective drug.
Results for those treated with drug B:

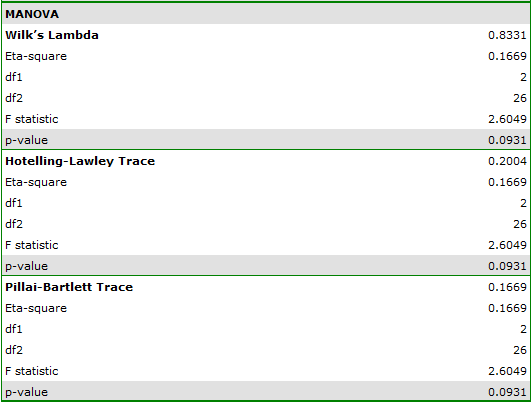
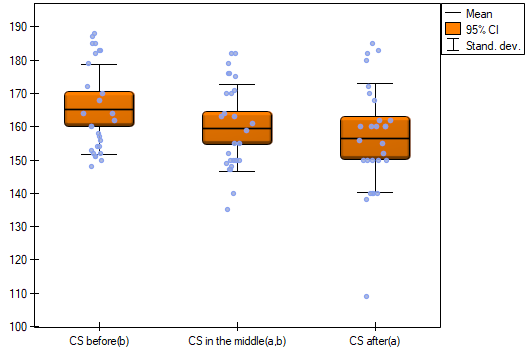
indicate that there are no significant differences between mean systolic blood pressure values, both when we use epsilon and Lambda Wilks (MANOVA) corrections. As little as 17% of the between-conditions variation in results can be explained by the use of drug B (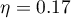 ).
).
2022/02/09 12:56
Mauchly's sphericity
Sphericity assumption is similar but stronger than the assumption of equality of variance. It is met if the variances for the differences between pairs of repeated measurements are the same. Usually, the simpler but more stringent compound symmetry condition is considered in place of the sphericity assumption. This can be done because meeting the compounded symmetry condition entails meeting the sphericity assumption.
Compound symmetry condition assumes, symmetry in the covariance matrix, and therefore equality of variances (elements of the main diagonal of the covariance matrix) and equality of covariances (elements off the main diagonal of the covariance matrix).
Violating the assumption of sphericity or combined symmetry unduly reduces the conservatism of the F-test (makes it easier to reject the null hypothesis).
To check the sphericity assumption, the Mauchly test is used (1940)\cite{mauchly}. Statistical significance (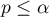 ) here implies a violation of the sphericity assumption.
) here implies a violation of the sphericity assumption.
Basic application conditions:
- measurement on an interval scale,
- multivariate normal distribution or normality of the distribution of each variable tested,
Hypotheses:
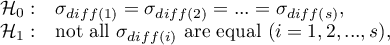
where:
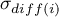 - population variance of differences between
- population variance of differences between  -th pair of repeated measurements,
-th pair of repeated measurements,
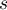 - number of pairs.
- number of pairs.
Mauchly's  value is defined as follows:
value is defined as follows:
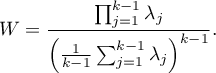
The test statistic has the form of:
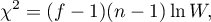
where:
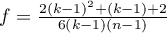 ,
,
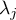 - eigenvalue of the expected covariance matrix,
- eigenvalue of the expected covariance matrix,
 - number of variables analyzed.
- number of variables analyzed.
This statistic has asymptotically (for large sample) Chi-square distribution with 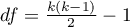 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

A value of 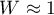 is an indication that the sphericity assumption is met. In interpreting the results of this test, however, it is important to note that it is sensitive to violations of the normality assumption of the distribution.
is an indication that the sphericity assumption is met. In interpreting the results of this test, however, it is important to note that it is sensitive to violations of the normality assumption of the distribution.
EXAMPLE (pressure.pqs file)
2022/02/09 12:56
2022/02/09 12:56
Non-parametric tests
The Kruskal-Wallis ANOVA
The Kruskal-Wallis one-way analysis of variance by ranks (Kruskal 1952 11); Kruskal and Wallis 1952 12)) is an extension of the U-Mann-Whitney test on more than two populations. This test is used to verify the hypothesis that there is no shift in the compared distributions, i.e., most often the insignificant differences between medians of the analysed variable in ( ) populations (but you need to assume, that the variable distributions are similar - comparison of rank variances can be checked using Conover's rank test).
) populations (but you need to assume, that the variable distributions are similar - comparison of rank variances can be checked using Conover's rank test).
Additional analyses:
- it is possible to test for a trend in the arrangement of the groups under study by performing the Jonckheere-Terpstra test for trend.
Basic assumptions:
- measurement on an ordinal scale or on an interval scale,
Hypotheses:
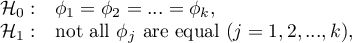
where:
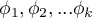 distributions of the analysed variable of each population.
distributions of the analysed variable of each population.
The test statistic is defined by:
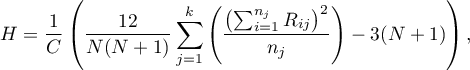
where:
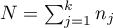 ,
,
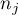 – samples sizes
– samples sizes  ,
,
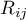 – ranks ascribed to the values of a variable for
– ranks ascribed to the values of a variable for 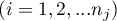 ,
,  ,
,
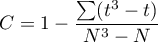 – correction for ties,
– correction for ties,
 – number of cases included in a tie.
– number of cases included in a tie.
The formula for the test statistic 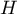 includes the correction for ties
includes the correction for ties  . This correction is used, when ties occur (if there are no ties, the correction is not calculated, because of
. This correction is used, when ties occur (if there are no ties, the correction is not calculated, because of  ).
).
The 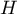 statistic asymptotically (for large sample sizes) has the Chi-square distribution with the number of degrees of freedom calculated using the formula:
statistic asymptotically (for large sample sizes) has the Chi-square distribution with the number of degrees of freedom calculated using the formula: 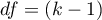 .
.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The POST-HOC tests
Introduction to the contrasts and the POST-HOC tests was performed in the unit, which relates to the one-way analysis of variance.
For simple comparisons, equal-size groups as well as unequal-size groups.
The Dunn test (Dunn 196413)) includes a correction for tied ranks (Zar 201014)) and is a test corrected for multiple testing. The Bonferroni or Sidak correction is most commonly used here, although other, newer corrections are also available, described in more detail in Multiple comparisons.
Example - simple comparisons (comparing 2 selected median / mean ranks with each other):
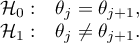
- [i] The value of critical difference is calculated by using the following formula:
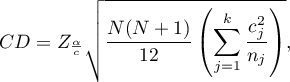
where:
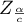 - is the critical value (statistic) of the normal distribution for a given significance level
- is the critical value (statistic) of the normal distribution for a given significance level  corrected on the number of possible simple comparisons
corrected on the number of possible simple comparisons  .
.
- [ii] The test statistic is defined by:
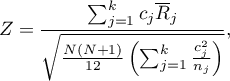
where:
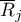 – mean of the ranks of the
– mean of the ranks of the  -th group, for
-th group, for  ,
,
The formula for the test statistic  includes a correction for tied ranks. This correction is applied when tied ranks are present (when there are no tied ranks this correction is not calculated because
includes a correction for tied ranks. This correction is applied when tied ranks are present (when there are no tied ranks this correction is not calculated because 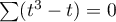 ).
).
The test statistic asymptotically (for large sample sizes) has the normal distribution, and the p-value is corrected on the number of possible simple comparisons  .
.
The non-parametric equivalent of Fisher LSD15), used for simple comparisons of both groups of equal and different sizes.
- [i] The value of critical difference is calculated by using the following formula:
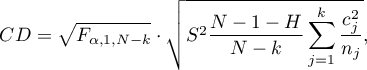
where:
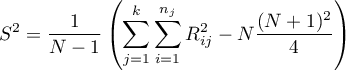
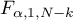 is the critical value (statistic) Snedecor's F distribution for a given significance level
is the critical value (statistic) Snedecor's F distribution for a given significance level  and for degrees of freedom respectively: 1 i
and for degrees of freedom respectively: 1 i 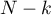 .
.
- [ii] The test statistic is defined by:
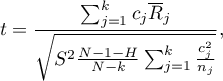
where:
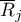 – The mean ranks of the
– The mean ranks of the  -th group, for
-th group, for  ,
,
This statistic follows a t-Student distribution with 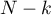 degrees of freedom.
degrees of freedom.
The settings window with the Kruskal-Wallis ANOVA can be opened in Statistics menu→NonParametric tests →Kruskal-Wallis ANOVA or in ''Wizard''.
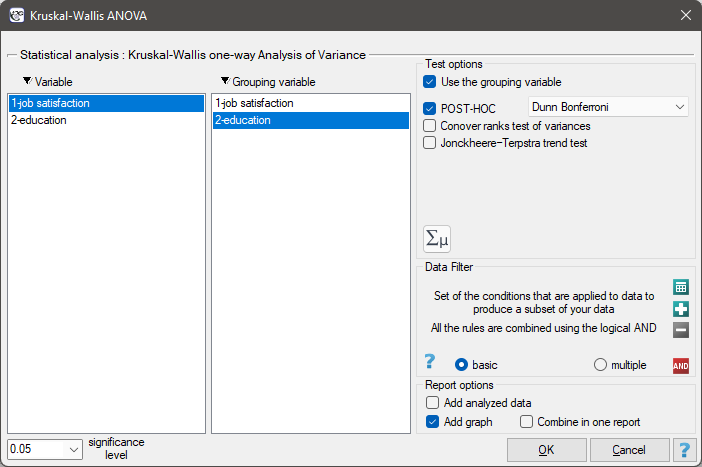
A group of 120 people was interviewed, for whom the occupation is their first job obtained after receiving appropriate education. The respondents rated their job satisfaction on a five-point scale, where:
1- unsatisfying job,
2- job giving little satisfaction,
3- job giving an average level of satisfaction,
4- job that gives a fairly high level of satisfaction,
5- job that is very satisfying.
We will test whether the level of reported job satisfaction does not change for each category of education.
Hypotheses:
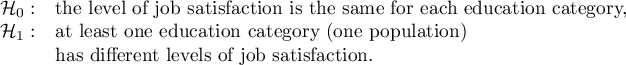

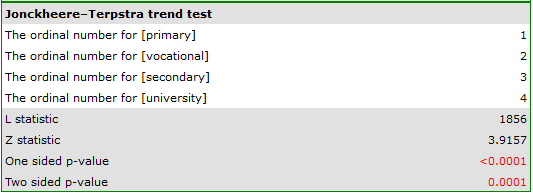
The obtained value of p=0.001 indicates a significant difference in the level of satisfaction between the compared categories of education. Dunn's POST-HOC analysis with Bonferroni's correction shows that significant differences are between those with primary and secondary education and those with primary and tertiary education. Slightly more differences can be confirmed by selecting the stronger POST-HOC Conover-Iman.
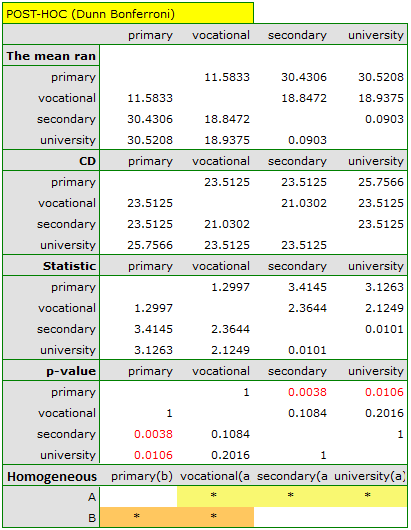
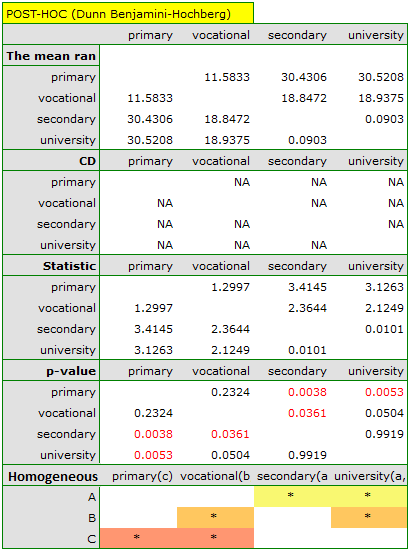
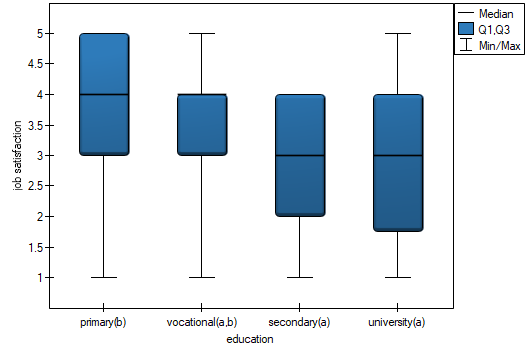
In the graph showing medians and quartiles we can see homogeneous groups determined by the POST-HOC test. If we choose to present Dunn's results with Bonferroni correction we can see two homogeneous groups that are not completely distinct, i.e. group (a) - people who rate job satisfaction lower and group (b)- people who rate job satisfaction higher. Vocational education belongs to both of these groups, which means that people with this education evaluate job satisfaction quite differently. The same description of homogeneous groups can be found in the results of the POST-HOC tests.
We can provide a detailed description of the data by selecting descriptive statistics in the analysis window 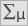 and indicating to add counts and percentages to the description.
and indicating to add counts and percentages to the description.
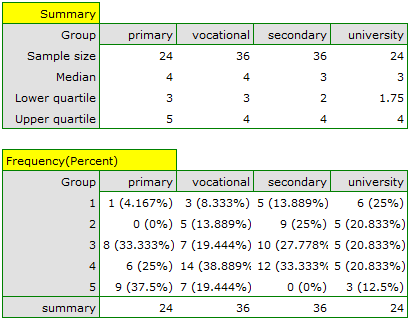
We can also show the distribution of responses in a column plot.
2022/02/09 12:56
The Jonckheere-Terpstra test for trend
The Jonckheere-Terpstra test for ordered alternatives described independently by Jonckheere (1954) 16) an be calculated in the same situation as the Kruskal-Wallis ANOVA , as it is based on the same assumptions. The Jonckheere-Terpstra test, however, captures the alternative hypothesis differently - indicating in it the existence of a trend for successive populations.
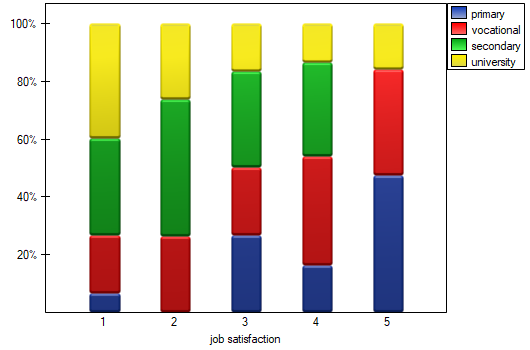
Hypotheses are simplified to medians:
Note
The term: „with at least one strict inequality” written in the alternative hypothesis of this test means that at least the median of one population should be greater than the median of another population in the order specified.
The test statistic has the form:
![LaTeX \begin{displaymath}
Z=\frac{L-\left[\frac{N^2-\sum_{j=1}^kn_j^2}{4}\right]}{SE}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img90c514ede7a37557872f285e3a796486.png)
where:
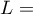 – sum of
– sum of 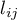 values obtained for each pair of compared populations,
values obtained for each pair of compared populations,
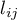 – number of results higher than a preset value in the next occurring group,
– number of results higher than a preset value in the next occurring group,
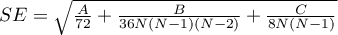 ,
,
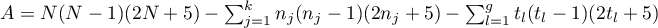 ,
,
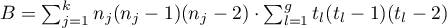 ,
,
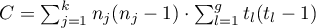 ,
,
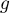 – number of groups of different tied ranks,
– number of groups of different tied ranks,
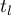 – umber of cases included in the tied rank,
– umber of cases included in the tied rank,
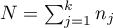 ,
,
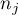 – sample sizes for
– sample sizes for  .
.
Note
To be able to perform a trend analysis, the expected order of the populations must be indicated by assigning consecutive natural numbers.
The formula for the test statistic  includes the correction for ties. This correction is applied when tied ranks are present (when there are no tied ranks the test statistic formula reduces to the original Jonckheere-Terpstra formula without this correction).
includes the correction for ties. This correction is applied when tied ranks are present (when there are no tied ranks the test statistic formula reduces to the original Jonckheere-Terpstra formula without this correction).
The statistic  has asymptotically (for large samples) normal distribution.
has asymptotically (for large samples) normal distribution.
With the expected direction of the trend known, the alternative hypothesis is one-sided and the one-sided p-value is interpreted. The interpretation of the two-sided p-value means that the researcher does not know (does not assume) the direction of the possible trend.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The settings window with the Jonckheere-Terpstra test for trend can be opened in Statistics menu→NonParametric tests→Kruskal-Wallis ANOVA or in ''Wizard''.
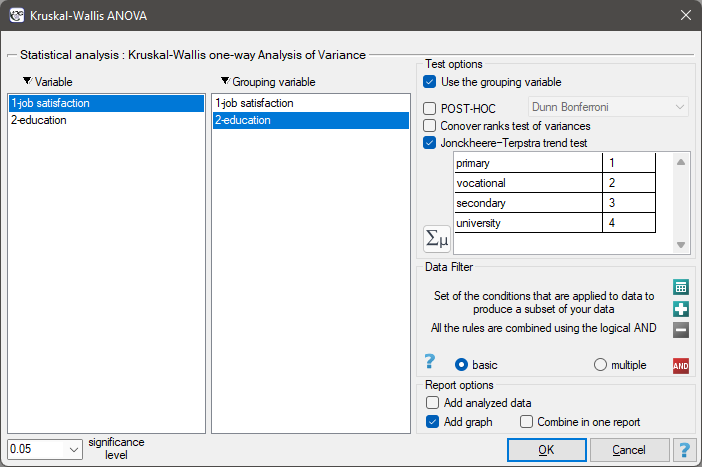
EXAMPLE cont. (jobSatisfaction.pqs file)
It is suspected that better educated people have high job demands, which may reduce the satisfaction level of the first job, which often does not meet such demands. Therefore, it is worthwhile to conduct a trend analysis.
Hypotheses:
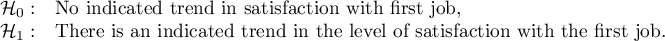
To do this, we resume the analysis with the  button, select the
button, select the Jonckheere-Terpstra trend test option, and assign successive natural numbers to the education categories.
The obtained one-sided value p<0.0001 and is less than the set significance level  , which speaks in favor of a trend actually occurring consistent with the researcher's expectations.
, which speaks in favor of a trend actually occurring consistent with the researcher's expectations.
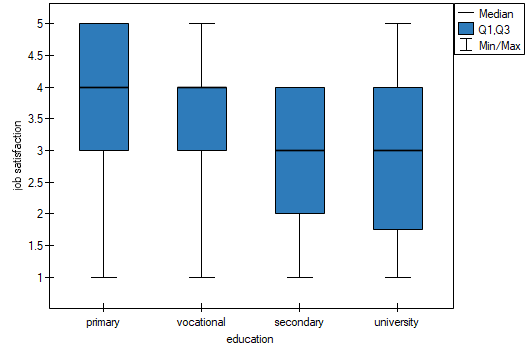
We can also confirm the existence of this trend by showing the percentage distribution of responses obtained.
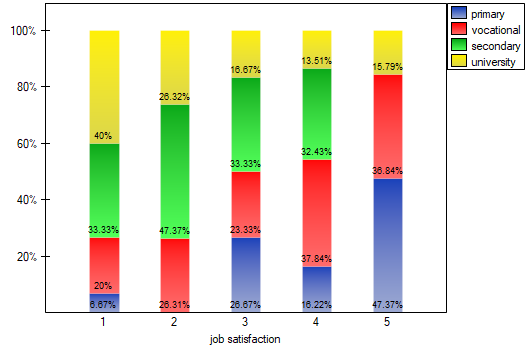
2022/02/09 12:56
The Conover ranks test of variance
Conover squared ranks test is used, similarly to Fisher-Snedecor test (for 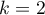 ), Levene test and Brown-Forsythe test (for
), Levene test and Brown-Forsythe test (for 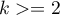 ) to verify the hypothesis of similar variation of the tested variable in several populations. It is the non-parametric counterpart of the tests indicated above, by that it does not assume normality of the data distribution and is based on the ranks17).However, this test examines variation and therefore distances to the mean, so the basic condition for its use is:
) to verify the hypothesis of similar variation of the tested variable in several populations. It is the non-parametric counterpart of the tests indicated above, by that it does not assume normality of the data distribution and is based on the ranks17).However, this test examines variation and therefore distances to the mean, so the basic condition for its use is:
- measurement on an interval scale,
Hypotheses:
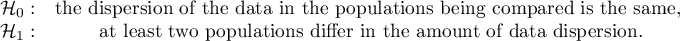
The test statistic has the form:
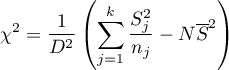
where:
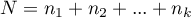 ,
,
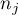 – individual group sizes,
– individual group sizes,
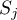 –sum of ranks squares in
–sum of ranks squares in  -th group,
-th group,
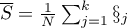 – mean of all ranks squares,
– mean of all ranks squares,
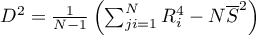 ,
,
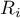 – ranks for values representing the distance of the measurement from the mean of a given group.
– ranks for values representing the distance of the measurement from the mean of a given group.
This statistic has a Chi-squaredistribution with 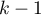 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The settings window with the Conover ranks test of variance can be opened in Statistics menu→NonParametric tests→Kruskal-Wallis ANOVA, option Conover ranks test of variance or textsf{Statistics} menu→NonParametric tests→Mann-Whitney, option Conover ranks test of variance.

EXAMPLE(surgeryMethod.pqs file)
Patients have been prepared for spinal surgery. The patients will be operated on by one of three methods. Preliminary allocation of each patient to each type of surgery has been made. At a later stage we intend to compare the condition of the patients after the surgeries, therefore we want the groups of patients to be comparable. They should be similar in terms of the height of the interbody space (WPMT) before surgery. The similarity should concern not only the average values but also the differentiation of the groups.
The distribution of the data was checked

It is found that for the two methods, the WPMT operation exhibits deviations from normality, largely caused by skewness of the data. Further comparative analysis will be conducted using the Kruskal-Wallis test to compare whether the level of WPMT differs between the methods, and the Conover test to indicate whether the spread of WPMT scores is similar in each method.
Hypotheses for Conover's variance test:
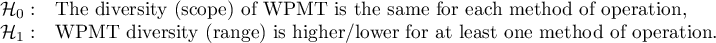
Hypotheses for Kruskal-Wallis test:
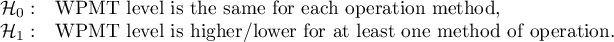


First, the value of Conover's test of variance is interpreted, which indicates statistically significant differences in the ranges of the groups compared (p=0.0022). From the graph, we can conclude that the differences are mainly in group 3. Since differences in WPMT were detected, the interpretation of the result of the Kruskal-Wallis test comparing the level of WPMT for these methods should be cautious, since this test is sensitive to heterogeneity of variance. Although the Kruskal-Wallis test showed no significant differences (p=0.2057), it is recommended that patients with low WPMT (who were mainly assigned to surgery with method B) be more evenly distributed, i.e. to see if they could be offered surgery with method A or C. After reassignment of patients, the analysis should be repeated.
2022/02/09 12:56
The Friedman ANOVA
The Friedman repeated measures analysis of variance by ranks – the Friedman ANOVA - was described by Friedman (1937)18). This test is used when the measurements of an analysed variable are made several times (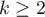 ) each time in different conditions. It is also used when we have rankings coming from different sources (form different judges) and concerning a few (
) each time in different conditions. It is also used when we have rankings coming from different sources (form different judges) and concerning a few ( ) objects, but we want to assess the grade of the rankings agreement.
) objects, but we want to assess the grade of the rankings agreement.
Iman Davenport (198019)) has shown that in many cases the Friedman statistic is overly conservative and has made some modification to it. This modification is the non-parametric equivalent of the ANOVA for dependent groups which makes it now recommended for use in place of the traditional Friedman statistic.
Additional analyses:
- It is possible to take missing data into account by using the Accept missing data option, calculating Durbin ANOVA or Skillings-Mack ANOVA;
- it is possible to test the trend in the arrangement of the studied groups by performing Page test for trend.
Basic assumptions:
- measurement on an ordinal scale or on an interval scale,
Hypotheses relate to the equality of the sum of ranks for successive measurements ( ) or are simplified to medians (
) or are simplified to medians (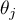 )
)
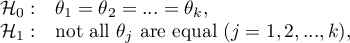
where:
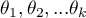 medians for an analysed features, in the following measurements from the examined population.
medians for an analysed features, in the following measurements from the examined population.
Two test statistics are determined: the Friedman statistic and the Iman-Davenport modification of this statistic.
The Friedman statistic has the form:
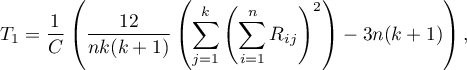
where:
 – sample size,
– sample size,
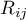 – ranks ascribed to the following measurements
– ranks ascribed to the following measurements  , separately for the analysed objects
, separately for the analysed objects 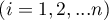 ,
,
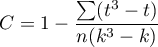 – correction for ties,
– correction for ties,
 – number of cases included in a tie.
– number of cases included in a tie.
The Iman-Davenport modification of the Friedman statistic has the form:
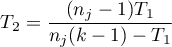
The formula for the test statistic 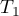 and
and 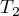 includes the correction for ties
includes the correction for ties  . This correction is used, when ties occur (if there are no ties, the correction is not calculated, because of
. This correction is used, when ties occur (if there are no ties, the correction is not calculated, because of 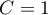 ).
).
The 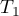 statistic has asymptotically (for large sample sizes) has the Chi-square distribution with
statistic has asymptotically (for large sample sizes) has the Chi-square distribution with 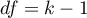 degrees of freedom.
degrees of freedom.
The statistic 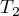 follows the Snedecor's F distribution with
follows the Snedecor's F distribution with 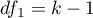 i
i  degrees of freedem.
degrees of freedem.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The POST-HOC tests
Introduction to the contrasts and the POST-HOC tests was performed in the unit, which relates to the one-way analysis of variance.
For simple comparisons (frequency in particular measurements is always the same).
The Dunn test (Dunn 196420)) is a corrected test due to multiple testing. The Bonferroni or Sidak correction is most commonly used here, although other, newer corrections are also available and are described in more detail in the Multiple Comparisons section.
Hypotheses:
Example - simple comparisons (comparison of 2 selected medians):
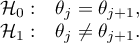
- [i] The value of critical difference is calculated by using the following formula:
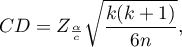
where:
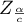 - is the critical value (statistic) of the normal distribution for a given significance level
- is the critical value (statistic) of the normal distribution for a given significance level  corrected on the number of possible simple comparisons
corrected on the number of possible simple comparisons  .
.
- [ii] The test statistic is defined by:
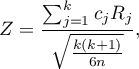
where:
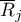 – mean of the ranks of the
– mean of the ranks of the  -th measurement, for
-th measurement, for  ,
,
The test statistic asymptotically (for large sample size) has normal distribution, and the p-value is corrected on the number of possible simple comparisons  .
.
Non-parametric equivalent of Fisher LSD21), sed for simple comparisons (counts across measurements are always the same).
- [i] he value of critical difference is calculated by using the following formula:
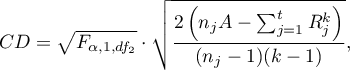
where:
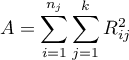 – sum of squares for ranks,
– sum of squares for ranks,
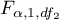 to critical value (statistic) Snedecor's F distribution for a given significance level
to critical value (statistic) Snedecor's F distribution for a given significance level  and for degrees of freedom respectively: 1 and
and for degrees of freedom respectively: 1 and 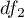 .
.
- [ii] The test statistic is defined by:
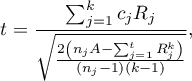
where:
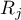 – the sum of ranks of
– the sum of ranks of  th measurement, for
th measurement, for  ,
,
The test statistic hast-Student distribution with 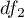 degrees of freedem.
degrees of freedem.
The settings window with the Friedman ANOVA can be opened in Statistics menu→NonParametric tests →Friedman ANOVA, trend test or in ''Wizard''
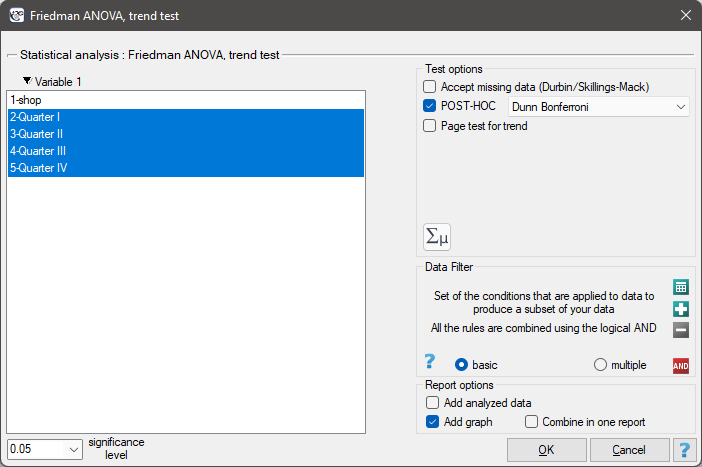
EXAMPLE (chocolate bar.pqs file)
Quarterly sale of some chocolate bar was measured in 14 randomly chosen supermarkets. The study was started in January and finished in December. During the second quarter, the billboard campaign was in full swing. Let's check if the campaign had an influence on the advertised chocolate bar sale.
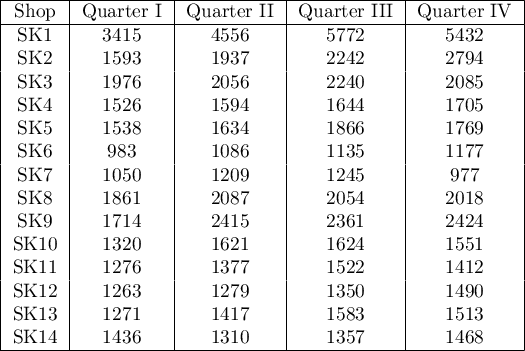
Hypotheses:


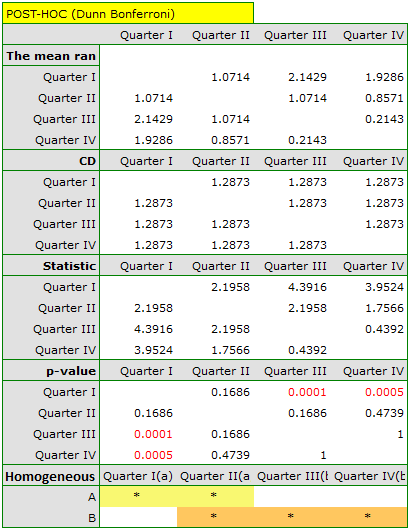
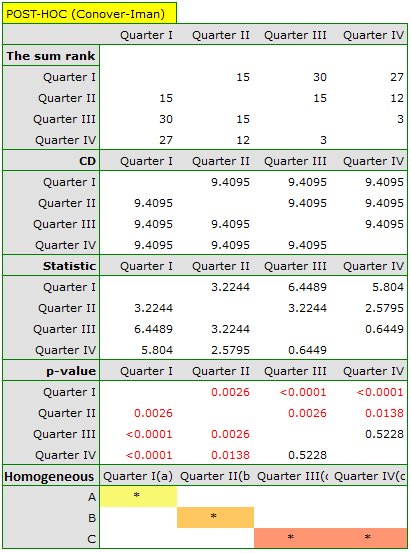
Comparing the p-value of the Friedman test (as well as the p-value of the Iman-Davenport correction of the Friedman test) with a significance level  , we find that sales of the bar are not the same in each quarter. The POST-HOC Dunn analysis performed with the Bonferroni correction indicates differences in sales volumes pertaining to quarters I and III and I and IV, and an analogous analysis performed with the stronger Conover-Iman test indicates differences between all quarters except quarters III and IV.
, we find that sales of the bar are not the same in each quarter. The POST-HOC Dunn analysis performed with the Bonferroni correction indicates differences in sales volumes pertaining to quarters I and III and I and IV, and an analogous analysis performed with the stronger Conover-Iman test indicates differences between all quarters except quarters III and IV.
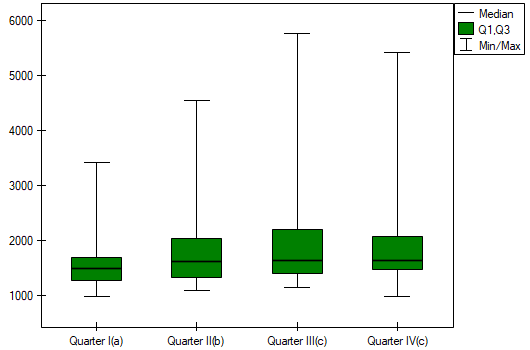
In the graph, we presented homogeneous groups determined by the Conover-Iman test.
We can provide a detailed description of the data by selecting Descriptive statistics in the analysis window  .
.
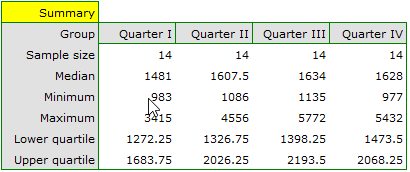
If the data were described by an ordinal scale with few categories, it would be useful to present it also in numbers and percentages. In our example, this would not be a good method of description.
2022/02/09 12:56
The Page test for trend
The Page test for ordered alternative described in 1963 by Page E. B. 22) can be computed in the same situation as Friedman's ANOVA, since it is based on the same assumptions. However, Page's test captures the alternative hypothesis differently - indicating that there is a trend in subsequent measurements.
Hypotheses involve equality of the sum of ranks for successive measurements or are simplified to medians:
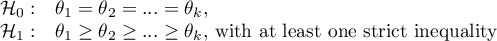
Note
The term: „with at least one strict inequality” written in the alternative hypothesis of this test means that at least one median should be greater than the median of another group of measurements in the order specified.
The test statistic has the form:
![LaTeX \begin{displaymath}
Z=\frac{L-\left[\frac{nk(k+1)^2}{4}\right]}{\sqrt{\frac{n(k^3-k)^2}{144(k-1)}}}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/imgd8f373e9725654f26c78c01931a87148.png)
where:
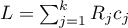 ,
,
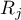 – the sum of ranks of
– the sum of ranks of  th measurement,
th measurement,
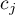 –the weight for
–the weight for  -th measurement informing about the natural order of this measurement among other measurements (weights are consecutive natural numbers).
-th measurement informing about the natural order of this measurement among other measurements (weights are consecutive natural numbers).
Note
In order to perform a trend analysis, the expected ordering of measurements must be indicated by assigning consecutive natural numbers to successive measurement groups. These numbers are treated as weights in the analysis 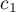 ,
, 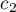 , …,
, …, 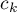 .
.
The formula for the test statistic  does not include a correction for ties, making it somewhat more conservative when tied ranks are present. However, using a correction for tied ranks for this test is not recommended.
does not include a correction for ties, making it somewhat more conservative when tied ranks are present. However, using a correction for tied ranks for this test is not recommended.
The statistic  has asymptotically (for large sample) normal distribution.
has asymptotically (for large sample) normal distribution.
With the expected direction of the trend known, the alternative hypothesis is one-sided and the one-sided p-value is interpreted. Interpreting a two-sided p-value means that the researcher does not know (does not assume) the direction of the possible trend.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The settings window with the Page test for trend can be opened in Statistics menu→NonParametric tests →Friedman ANOVA, trend test or in ''Wizard''
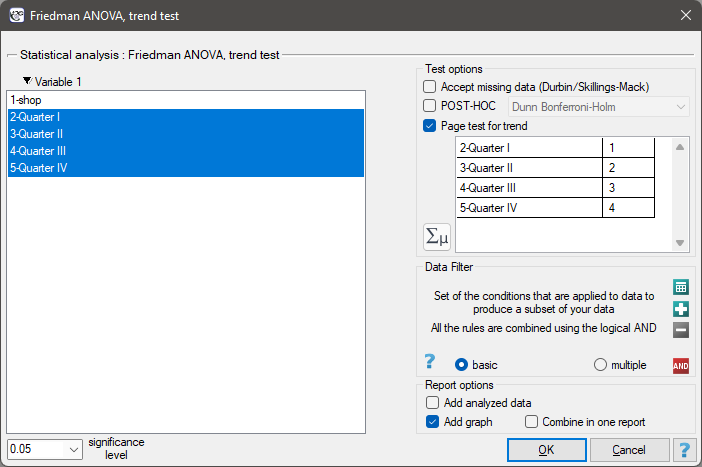
EXAMPLE cont. (chocolate bar.pqs file)
The expected result of the intensive advertising campaign conducted by the company is a steady increase in sales of the offered bar.
Hypotheses:
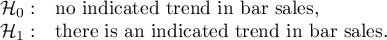
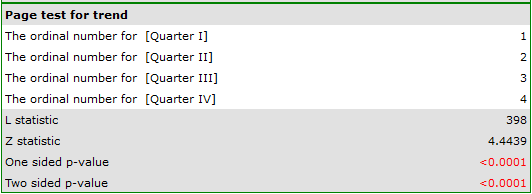
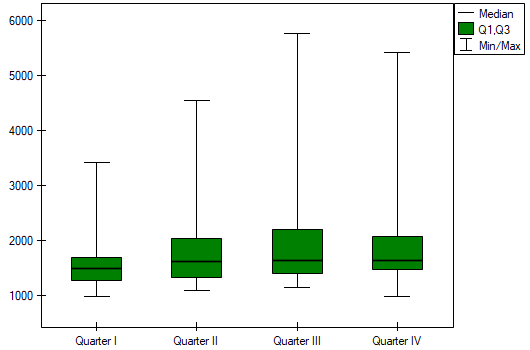
Comparing a one-sided p<0.0001 with a significance level  , we find that the campaign produced the expected trend of increased product sales.
, we find that the campaign produced the expected trend of increased product sales.
2022/02/09 12:56
The Durbin's ANOVA (missing data)
Durbin's analysis of variance of repeated measurements for ranks was proposed by Durbin (1951)23). This test is used when measurements of the variable under study are made several times – a similar situation in which Friedman'sANOVA is used. The original Durbin test and the Friedman test give the same result when we have a complete data set. However, Durbin's test has an advantage – it can also be calculated for an incomplete data set. At the same time, data deficiencies cannot be located arbitrarily, but the data must form a so-called balanced and incomplete block:
- the number of measurements for each object is
 (
(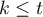 ),
), - each measurement is made on
 objects (
objects (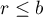 ),
), - the number of objects for which the same pair of measurements was taken simultaneously is constant and equal to
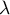 .
.
where:
 – total number of considered measurements,
– total number of considered measurements,
 – total number of examined objects.
– total number of examined objects.
Basic assumptions:
- measurement on an ordinal scale or on an interval scale,
Hypotheses involve equality of the sum of ranks for successive measurements (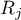 ) or are simplified to medians (
) or are simplified to medians (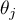 ):
):
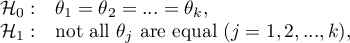
Two test statistics of the following form are determined:
![LaTeX \begin{displaymath}
T_1=\frac{(t-1)\left[\sum_{j=1}^tR_j^2-tC\right]}{A-C},
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img6263bdbeddade6aabd733985ed7a7916.png)
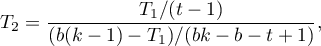
where:
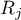 – sum of ranks for successive measurements
– sum of ranks for successive measurements 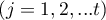 ,
,
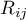 – ranks assigned to successive measurements, separately for each of the studied objects
– ranks assigned to successive measurements, separately for each of the studied objects 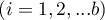 ,
,
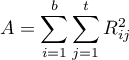 – sum of squared ranks,
– sum of squared ranks,
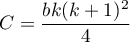 – correction coefficient.
– correction coefficient.
The formula for  and
and  statistics includes a correction for tied ranks.
statistics includes a correction for tied ranks.
For complete data, the 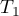 statistic is the same as the Friedman test. It has asymptotically (for large sample sizes) Chi-square distribution with
statistic is the same as the Friedman test. It has asymptotically (for large sample sizes) Chi-square distribution with 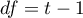 degrees of freedom.
degrees of freedom.
The 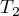 statistic is the equivalent of Friedman's Iman-Davenport ANOVA adjustment, so it follows Snedecor's F distribution with
statistic is the equivalent of Friedman's Iman-Davenport ANOVA adjustment, so it follows Snedecor's F distribution with 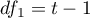 i
i  degrees of freedom. It is now considered to be more precise than the
degrees of freedom. It is now considered to be more precise than the 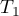 statistic and is recommended for use with the
statistic and is recommended for use with the 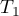 statistic24).
statistic24).
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

Testy POST-HOC
Introduction to the contrasts and the POST-HOC tests was performed in the unit, which relates to the one-way analysis of variance.
Used for simple comparisons (the counts in each measurement are always the same).
Hypotheses:
Example - simple comparisons (comparing 2 selected medians / rank sums between each other):
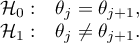
- [ii] The value of critical difference is calculated by using the following formula:
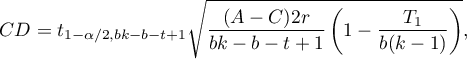
where:
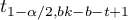 – is the [wartosc_krytyczna|critical value (statistic) of the t-Student distribution for a given significance level
– is the [wartosc_krytyczna|critical value (statistic) of the t-Student distribution for a given significance level  and
and 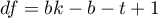 degrees of freedom.
degrees of freedom.
- [ii] The test statistic has the form:
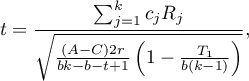
The test statistic has t-Student distribution with 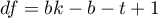 degrees of freedom.
degrees of freedom.
The settings window with the Durbin's ANOVA can be opened in Statistics menu→NonParametric tests →Friedman ANOVA, trend test or in ''Wizard''
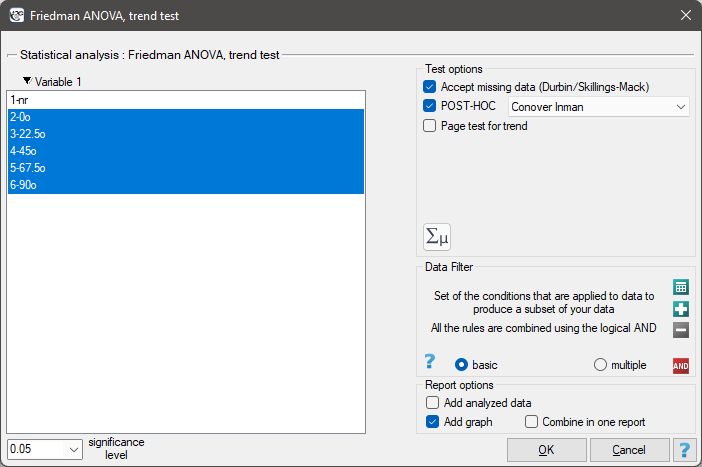
Note
For records with missing data to be taken into account, you must check the Accept missing data option. Empty cells and cells with non-numeric values are treated as missing data. Only records with more than one numeric value will be analyzed.
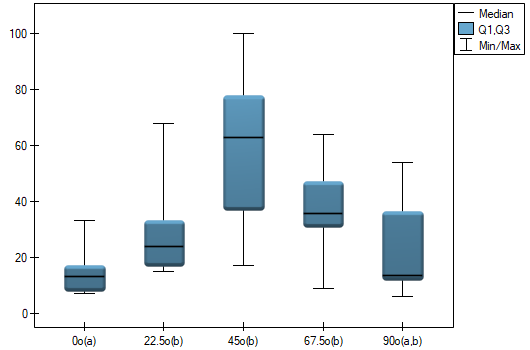
An experiment was conducted among 20 patients in a psychiatric hospital (Ogilvie 1965)25). This experiment involved drawing straight lines according to a presented pattern. The pattern represented 5 lines drawn at different angles (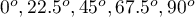 ) relative to the indicated center. The patients' task was to reproduce the lines while having their hand covered. The time at which the patient drew the line was recorded as the result of the experiment. Ideally, each patient would draw a line from all angles, but elapsed time and fatigue would have a significant impact on performance. In addition, it is difficult to keep the patient interested and willing to cooperate for an extended period of time. Therefore, the project was planned and conducted in balanced and incomplete blocks. Each of the 20 patients traced a line at two angles (there were five possible angles). Thus, each angle was drawn eight times. The time at which each patient drew a line at a given angle was recorded in the table.
) relative to the indicated center. The patients' task was to reproduce the lines while having their hand covered. The time at which the patient drew the line was recorded as the result of the experiment. Ideally, each patient would draw a line from all angles, but elapsed time and fatigue would have a significant impact on performance. In addition, it is difficult to keep the patient interested and willing to cooperate for an extended period of time. Therefore, the project was planned and conducted in balanced and incomplete blocks. Each of the 20 patients traced a line at two angles (there were five possible angles). Thus, each angle was drawn eight times. The time at which each patient drew a line at a given angle was recorded in the table.
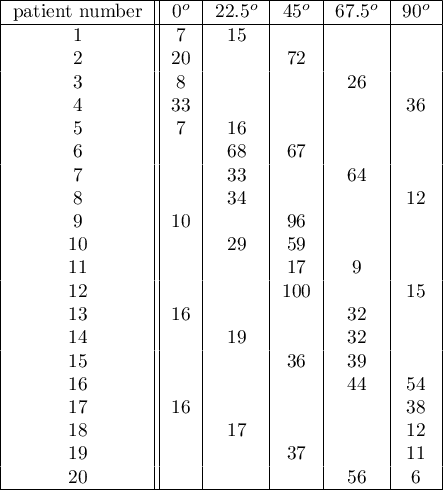
We want to see if the time taken to draw each line is completely random, or if there are lines that took more or less time to draw.
Hypotheses:
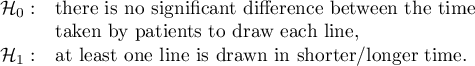
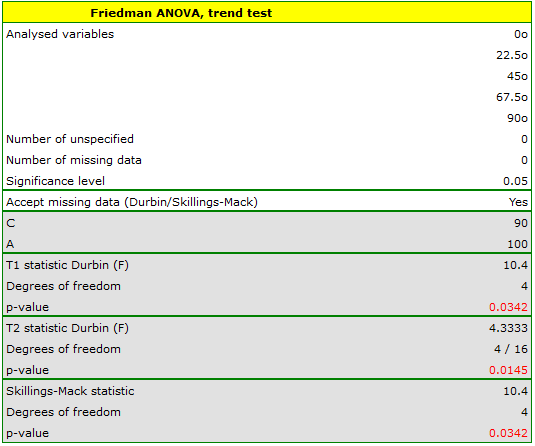
Comparing the p=0.0145 for the 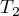 statistic (or the p=0.0342 for the
statistic (or the p=0.0342 for the 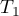 statistic) with the
statistic) with the  significance level, we find that the lines are not drawn at the same time. The POST-HOC analysis performed indicates that there is a difference in the time taken to draw the line at angle
significance level, we find that the lines are not drawn at the same time. The POST-HOC analysis performed indicates that there is a difference in the time taken to draw the line at angle 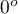 . It is drawn faster than the lines at the angle of
. It is drawn faster than the lines at the angle of 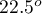 ,
, 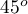 and
and 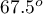 .
.
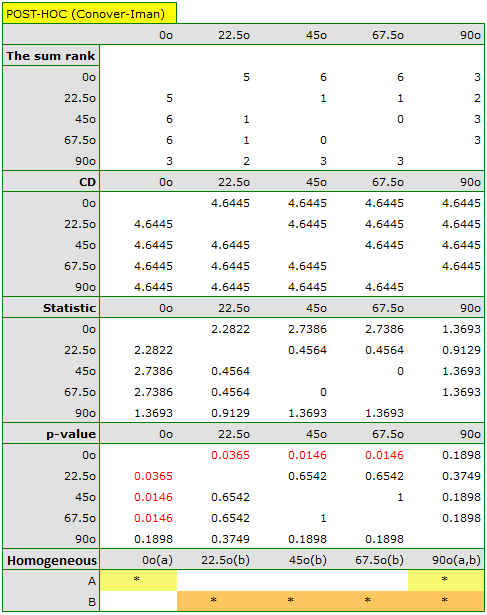
The graph shows homogeneous groups indicated by the post-hoc test.
2022/02/09 12:56
The Skillings-Mack ANOVA (missing data)
The analysis of variance of repeated measures for Skillings-Mack ranks was proposed by Skillings and Mack in 1981 26). t is a test that can be used when there are missing data, but the missing data need not occur in any particular setting. However, each site must have at least two observations. If there are no tied ranks and no gaps are present it is the same as the Friedman's ANOVA, and if data gaps are present in a balanced arrangement it corresponds to the results of Durbin's ANOVA.
Basic assumptions: Basic assumptions:
- measurement on an ordinal scale or on an interval scale,
Hypotheses relate to the equality of the sum of ranks for successive measurements ( ) or are simplified to medians (
) or are simplified to medians ( )
)
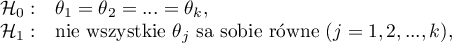
The test statistic has the form:
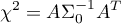
where:
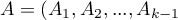
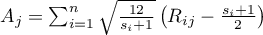 ,
,
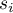 – number of observations for
– number of observations for  -th object,
-th object,
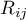 – ranks assigned to successive measurements (
– ranks assigned to successive measurements (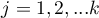 ), separately for each study object (
), separately for each study object (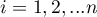 ), with ranks for missing data equal to the average rank for the object,
), with ranks for missing data equal to the average rank for the object,
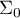 – matrix determining the covariances for
– matrix determining the covariances for 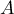 at the truth of
at the truth of 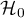 27).
27).
When each pair of measurements occurs simultaneously for at least one observation, this statistic has asymptotically (for large sample sizes) the Chi-square distribution with 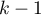 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The settings window with the Skillings-Mack ANOVA can be opened in Statistics menu→NonParametric tests →Friedman ANOVA, trend test or in ''Wizard''
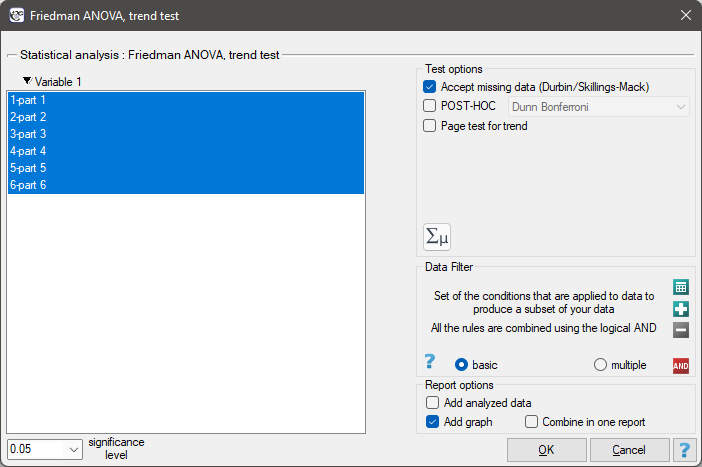
Note
For records with missing data to be taken into account, you must check the Accept missing data option. Empty cells and cells with non-numeric values are treated as missing data. Only records containing more than one numeric value will be analyzed.
A certain university teacher, wanting to improve the way he conducted his classes, decided to verify his teaching skills. In several randomly selected student groups, during the last class, he asked them to fill in a short anonymous questionnaire. The survey consisted of six questions about how the six specified parts of the material were illustrated. The students could rate it on a 5-point scale, where 1 - the way of presenting the material was completely incomprehensible, 5 - a very clear and interesting way of illustrating the material. The data obtained in this way turned out to be incomplete due to the fact that students did not answer questions about the part of the material they were absent on. In the 30-person group completing the survey, only 15 students provided complete responses. Performing an analysis that does not account for data gaps (in this case, a Friedman analysis) will have limited power by cutting the group size so drastically and will not lead to the detection of significant differences. Data gaps were not planned for and are not present in the balanced block, so this task cannot be performed using Durbin's analysis along with his POST-HOC test.
Hypotheses:
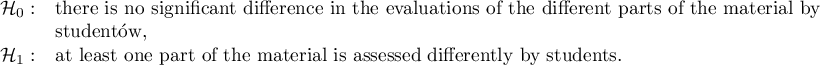
The results of the ANOVA Skillings-Mack analysis are presented in the following report:
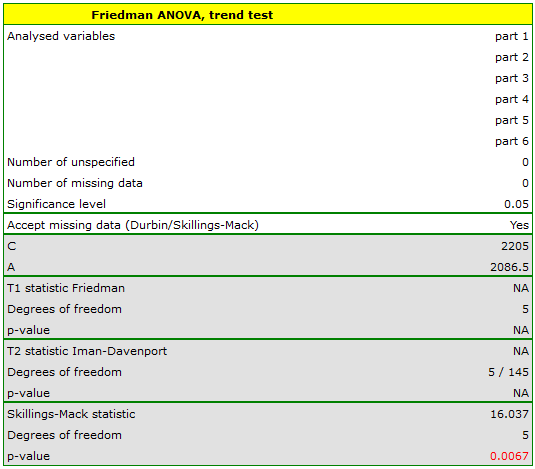
The  value obtained should be treated with caution due to possible tied ranks. However, for this study, the p=0.0067 is well below the accepted significance level of
value obtained should be treated with caution due to possible tied ranks. However, for this study, the p=0.0067 is well below the accepted significance level of  , indicating that significant differences exist. The differences in responses can be observed in the graph; however, there is no POST-HOC analysis available for this test.
, indicating that significant differences exist. The differences in responses can be observed in the graph; however, there is no POST-HOC analysis available for this test.
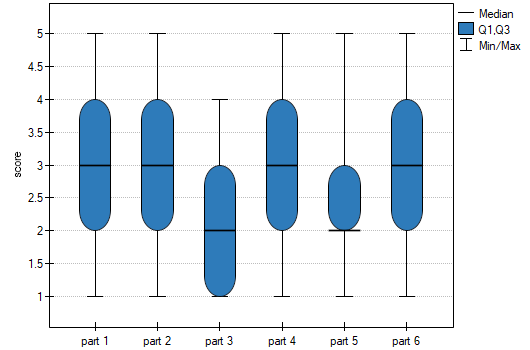
2022/02/09 12:56
The Chi-square test for multidimensional contingency tables
Basic assumptions:
- measurement on a nominal scale - any order is not taken into account,
Hypotheses:
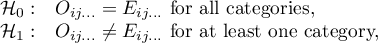
where:
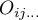 and
and 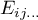
 observed frequencies in a contingency table and the corresponding expected frequencies.
observed frequencies in a contingency table and the corresponding expected frequencies.
The test statistic is defined by:
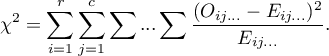
This statistic asymptotically (for large expected frequencies) has the Chi-square distribution with a number of degrees of freedom calculated using the formula: 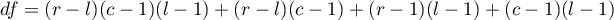 - for 3-dimensional tables.
- for 3-dimensional tables.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The settings window with the Chi-square (multidimensional) test can be opened in Statistics menu → NonParametric tests (unordered categories)→Chi-square (multidimensional) or in ''Wizard''.
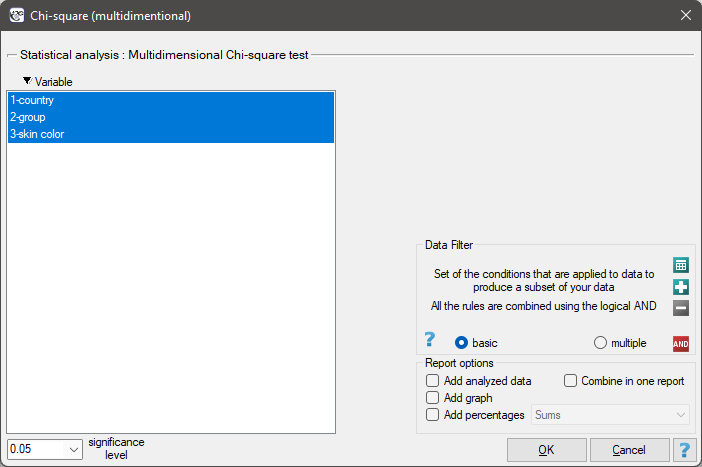
Note
This test can be calculated only on the basis of raw data.
2022/02/09 12:56
The Q-Cochran ANOVA
The Q-Cochran analysis of variance, based on the Q-Cochran test, is described by Cochran (1950)29). This test is an extended McNemar test for 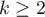 dependent groups. It is used in hypothesis verification about symmetry between several measurements
dependent groups. It is used in hypothesis verification about symmetry between several measurements  for the
for the  feature. The analysed feature can have only 2 values - for the analysis, there are ascribed to them the numbers: 1 and 0.
feature. The analysed feature can have only 2 values - for the analysis, there are ascribed to them the numbers: 1 and 0.
Basic assumptions:
- measurement on a nominal scale (dichotomous variables – it means the variables of two categories),
Hypotheses:
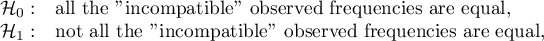
where:
„incompatible” observed frequencies – the observed frequencies calculated when the value of the analysed feature is different in several measurements.
The test statistic is defined by:
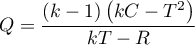
where:
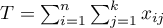 ,
,
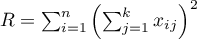 ,
,
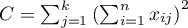 ,
,
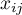 – the value of
– the value of  -th measurement for
-th measurement for  -th object (so 0 or 1).
-th object (so 0 or 1).
This statistic asymptotically (for large sample size) has the Chi-square distribution with a number of degrees of freedom calculated using the formula: 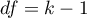 .
.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The POST-HOC tests
Introduction to the contrasts and the POST-HOC tests was performed in the unit, which relates to the one-way analysis of variance.
For simple comparisons (frequency in particular measurements is always the same).
Hypotheses:
Example - simple comparisons (for the difference in proportion in a one chosen pair of measurements):
- [i] The value of critical difference is calculated by using the following formula:
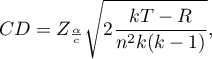
where:
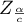 - is the critical value (statistic) of the normal distribution for a given significance level
- is the critical value (statistic) of the normal distribution for a given significance level  corrected on the number of possible simple comparisons
corrected on the number of possible simple comparisons  .
.
</WRAP
- [ii] The test statistic is defined by:
where:
 – the proportion
– the proportion  -th measurement
-th measurement  ,
,
The test statistic asymptotically (for large sample size) has the normal distribution, and the p-value is corrected on the number of possible simple comparisons  .
.
The settings window with the Cochran Q ANOVA can be opened in Statistics menu→ NonParametric tests→Cochran Q ANOVA or in ''Wizard''.

Note
This test can be calculated only on the basis of raw data.
We want to compare the difficulty of 3 test questions. To do this, we select a sample of 20 people from the analysed population. Every person from the sample answers 3 test questions. Next, we check the correctness of answers (an answer can be correct or wrong). In the table, there are following scores:
Hypotheses:

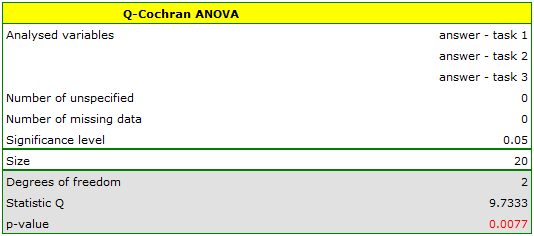
Comparing the p value p=0.0077 with the significance level  we conclude that individual test questions have different difficulty levels. We resume the analysis to perform POST-HOC test by clicking
we conclude that individual test questions have different difficulty levels. We resume the analysis to perform POST-HOC test by clicking  , and in the test option window, we select POST-HOC
, and in the test option window, we select POST-HOC Dunn.

The carried out POST-HOC analysis indicates that there are differences between the 2-nd and 1-st question and between questions 2-nd and 3-th. The difference is because the second question is easier than the first and the third ones (the number of correct answers the first question is higher).
2022/02/09 12:56
2022/02/09 12:56
1)
Lund R.E., Lund J.R. (1983), Algorithm AS 190, Probabilities and Upper Quantiles for the Studentized Range. Applied Statistics; 34
2)
Brown M. B., Forsythe A. B. (1974), The small sample behavior of some statistics which test the equality of several means. Technometrics, 16, 385-389
3)
Welch B. L. (1951), On the comparison of several mean values: an alternative approach. Biometrika 38: 330–336
4)
Tamhane A. C. (1977), Multiple comparisons in model I One-Way ANOVA with unequal variances. Communications in Statistics, A6 (1), 15-32
5)
Brown M. B., Forsythe A. B. (1974), The ANOVA and multiple comparisons for data with heterogeneous variances. Biometrics, 30, 719-724
6)
Games P. A., Howell J. F. (1976), Pairwise multiple comparison procedures with unequal n's and/or variances: A Monte Carlo study. Journal of Educational Statistics, 1, 113-125
7)
Levene H. (1960), Robust tests for the equality of variance. In I. Olkin (Ed.) Contributions to probability and statistics (278-292). Palo Alto, CA: Stanford University Press
8)
Brown M.B., Forsythe A. B. (1974a), Robust tests for equality of variances. Journal of the American Statistical Association, 69,364-367
9)
Greenhouse S. W., Geisser S. (1959), On methods in the analysis of profile data. Psychometrika, 24, 95–112
10)
Huynh H., Feldt L. S. (1976), Estimation of the Box correction for degrees of freedom from sample data in randomized block and split=plot designs. Journal of Educational Statistics, 1, 69–82
11)
Kruskal W.H., Wallis W.A. (1952), Use of ranks in one-criterion variance analysis. Journal of the American Statistical Association, 47, 583-621
14)
Zar J. H., (2010), Biostatistical Analysis (Fifth Editon). Pearson Educational
15)
, 17)
, 21)
, 23)
Conover W. J. (1999), Practical nonparametric statistics (3rd ed). John Wiley and Sons, New York
16)
Jonckheere A. R. (1954), A distribution-free k-sample test against ordered alternatives. Biometrika, 41: 133–145) and Terpstra (1952)((Terpstra T. J. (1952), The asymptotic normality and consistency of Kendall's test against trend, when ties are present in one ranking. Indagationes Mathematicae, 14: 327–333
18)
Friedman M. (1937), The use of ranks to avoid the assumption of normality implicit in the analysis of variance. Journal of the American Statistical Association, 32,675-701
19)
Iman R. L., Davenport J. M. (1980), Approximations of the critical region of the friedman statistic, Communications in Statistics 9, 571–595
22)
Page E. B. (1963), Ordered hypotheses for multiple treatments: A significance test for linear ranks. Journal of the American Statistical Association 58 (301): 216–30
24)
Durbin J. (1951), Incomplete blocks in ranking experiments. British Journal of Statistical Psychology, 4: 85–90
25)
Ogilvie J. C. (1965), Paired comparison models with tests for interaction. Biometrics 21(3): 651-64
26)
, 27)
Skillings J.H., Mack G.A. (1981) On the use of a Friedman-type statistic in balanced and unbalanced block designs. Technometrics, 23:171–177
28)
Cochran W.G. (1952), The chi-square goodness-of-fit test. Annals of Mathematical Statistics, 23, 315-345
29)
Cochran W.G. (1950), The comparison ofpercentages in matched samples. Biometrika, 37, 256-266
en/statpqpl/porown3grpl.txt · ostatnio zmienione: 2022/02/12 16:23 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

