PQStat - Baza Wiedzy

Spis treści

Spatial weights matrix
- Weights matrix according to distance
- Weights matrix according to contiguity

Spatial weights matrix

Spatial relations among objects presented on a map can be organized in the form of a matrix. The matrices are called weights matrices. Due to their large size and a great amount of detailed information, weights matrices are not carriers of knowledge which could be presented directly in the results of a conducted study but they form the basis of further analysis. The data included in the matrices are usually treated as weights in spatial analyses and, in this manner, allow to use the information from the map.

The simplest form of a weights matrix is a neighbor matrix. Neighbor matrix is a square table with zeros on the main diagonal, where the neighborhood of objects is marked with a binary value (1 – for neighboring objects, 0 – for non-neighboring objects).

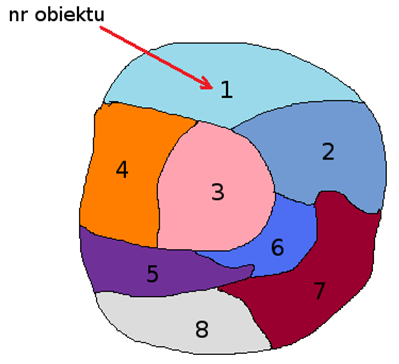
$\begin{tabular}{c|c|c|c|c|c|c|c|c|c|} \cline{2-10} \multirow{9}{*}{}} &\textbf{no} &\textbf{1} &\textbf{2} &\textbf{3} &\textbf{4} &\textbf{5} &\textbf{6} &\textbf{7} &\textbf{8}\\\cline{2-10} &\textbf{1} &0 &1 &1 &1 &0 &0 &0 &0\\\cline{2-10} &\textbf{2} &1 &0 &1 &0 &0 &1 &1 &0\\\cline{2-10} &\textbf{3} &1 &1 &0 &1 &1 &1 &0 &0\\\cline{2-10} &\textbf{4} &1 &0 &1 &0 &1 &0 &0 &0\\\cline{2-10} &\textbf{5} &0 &0 &1 &1 &0 &1 &1 &1\\\cline{2-10} &\textbf{6} &0 &1 &1 &0 &1 &0 &1 &1\\\cline{2-10} &\textbf{7} &0 &1 &0 &0 &1 &1 &0 &1\\\cline{2-10} &\textbf{8} &0 &0 &0 &0 &1 &1 &1 &0 \\\cline{2-10} \end{tabular}$

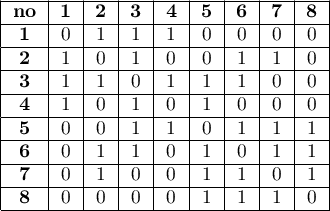
In statistical analyses the most commonly used matrices are row-standardized matrices with the values of each of its rows summing to one. Row standardization means that each weight is divided by the sum of a row (the sum of the weights of all neighboring elements). As a result, the obtained weights are in the range from 0 to 1. The influence of objects with varying numbers of neighbors, in analyses based on a weights matrix standardized in this way, is balanced.

$\begin{tabular}{|c|c|c|c|c|c|c|c|c|}\hline \textbf{no} &\textbf{1} &\textbf{2} &\textbf{3} &\textbf{4} &\textbf{5} &\textbf{6} &\textbf{7} &\textbf{8}\\\hline \textbf{1} &0 &$1/3$ &$1/3$ &$1/3$ &0 &0 &0 &0\\\hline \textbf{2} &$1/4$ &0 &$1/4$ &0 &0 &$1/4$ &$1/4$ &0\\\hline \textbf{3} &$1/5$ &$1/5$ &0 &$1/5$ &$1/5$ &$1/5$ &0 &0\\\hline \textbf{4} &$1/3$ &0 &$1/3$ &0 &$1/3$ &0 &0 &0\\\hline \textbf{5} &0 &0 &$1/5$ &$1/5$ &0 &$1/5$ &1/5 &$1/5$\\\hline \textbf{6} &0 &$1/5$ &$1/5$ &0 &$1/5$ &0 &$1/5$ &$1/5$\\\hline \textbf{7} &0 &$1/4$ &0 &0 &$1/4$ &$1/4$ &0 &$1/4$\\\hline \textbf{8} &0 &0 &0 &0 &$1/3$ &$1/3$ &$1/3$ &0 \\\hline \end{tabular}$

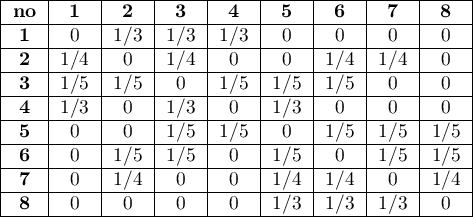
Selected weights matrices should reflect spatial relationships which connect the analyzed objects. The more realistic the reflection of the model of mutual influence of objects in space, the more exact results will be obtained.

The window with settings for weights matrices is accessed via the menu Spacial analysis→Tools→Spatial weights matrix.

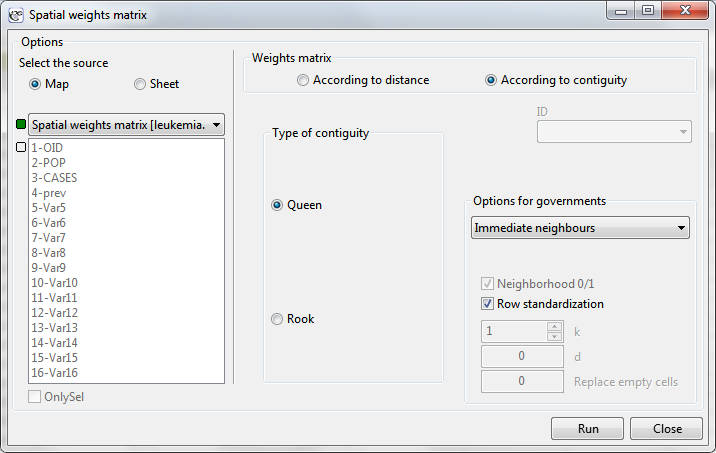
Weights matrix according to distance

For creating a weights matrix based on the distances of points we should have at our disposal data from a map which contains objects such as a point, a multipoint, or a polygon. In the case of an analysis of polygons, calculations are based on centroids, and in the case of multipoints they are based on centers of objects.

Description you can find in User Guide - PQStat, section: the similarity matrix.

2022/02/09 12:56

Weights matrix according to contiguity

For creating a weights matrix based on proximity of objects (contiguity) we should have at our disposal data from a map which contains objects such as a multipoint or a polygon.

Type of contiguity

The contiguity is usually understood as a common section with a non-zero length (i.e. a section longer than 1 point) – it is the Rook type neighborhood, or as any section (also of zero length, i.e. a point) – it is the Queen type neighborhood.

Weights matrix according to contiguity:

Direct neighbors – it is a square symmetrical matrix in which on the main diagonal there are zeros, the elements outside the diagonal are:
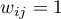- $w_{ij} = 1$ -– if the objects are connected along a common border,
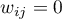- $w_{ij} = 0$ -– in the opposite case.
Neighbors (order of contiguity ⇐k) -– it is a square symmetrical matrix in which on the main diagonal there are zeros, the elements outside the diagonal are:
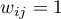- $w_{ij} = 1$ -– if the objects are direct neighbors (they are connected along a common border),
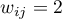- $w_{ij} = 2$ -– if the objects are the second nearest neighbors (the second degree of neighborhood, i.e. the so-called neighbor's neighbor)
- …
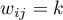- $w_{ij} = k$ -– if the objects are the 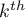$k^{th}$ neighbors ( 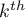$k^{th}$ degree of neighborhood)
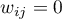- $w_{ij} = 0$ -– neighborhood is farther than the 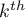$k^{th}$ degree.
Neighbors (order of contiguity =k) -– it is a square symmetrical matrix in which on the main diagonal there are zeros, the elements outside the diagonal are:
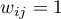- $w_{ij} = 1$ -– if the objects are the 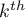$k^{th}$ neighbors ( 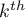$k^{th}$ degree of neighborhood)
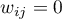- $w_{ij} = 0$ -– in the opposite case.