PQStat - Baza Wiedzy

Spis treści

Macierz wag przestrzennych
- Macierz wag według odległości
- Macierz wag według wspólnej granicy

Macierz wag przestrzennych

Wzajemne relacje przestrzenne pomiędzy obiektami przedstawionymi na płaszczyźnie mapy mogą zostać przełożone na postać macierzową. Uzyskane macierze nazywane są macierzami wag. Ze względu na duże rozmiary i dużą ilość szczegółowej informacji, macierze wag nie są nośnikiem wiedzy, która może być bezpośrednio zamieszczona w wynikach przeprowadzanego badania, ale stanowią bazę do dalszych analiz. Zawarte w nich dane traktowane są zwykle w analizach przestrzennych jako wagi i w ten sposób pozwalają wykorzystać informacje płynące z mapy.

Najprostszą postacią macierzy wag jest macierz sąsiedztwa. Macierz sąsiedztwa jest tablicą kwadratową o zerach na diagonali, gdzie sąsiedztwo pomiędzy obiektami jest oznaczane wartością binarną (1 – gdy obiekty sąsiadują, 0 – gdy obiekty nie sąsiadują).

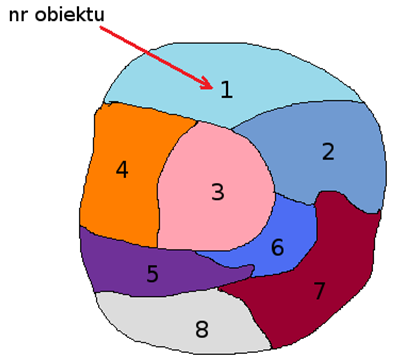
$\begin{tabular}{c|c|c|c|c|c|c|c|c|c|} \cline{2-10} \multirow{9}{*}{}} &\textbf{nr} &\textbf{1} &\textbf{2} &\textbf{3} &\textbf{4} &\textbf{5} &\textbf{6} &\textbf{7} &\textbf{8}\\\cline{2-10} &\textbf{1} &0 &1 &1 &1 &0 &0 &0 &0\\\cline{2-10} &\textbf{2} &1 &0 &1 &0 &0 &1 &1 &0\\\cline{2-10} &\textbf{3} &1 &1 &0 &1 &1 &1 &0 &0\\\cline{2-10} &\textbf{4} &1 &0 &1 &0 &1 &0 &0 &0\\\cline{2-10} &\textbf{5} &0 &0 &1 &1 &0 &1 &1 &1\\\cline{2-10} &\textbf{6} &0 &1 &1 &0 &1 &0 &1 &1\\\cline{2-10} &\textbf{7} &0 &1 &0 &0 &1 &1 &0 &1\\\cline{2-10} &\textbf{8} &0 &0 &0 &0 &1 &1 &1 &0 \\\cline{2-10} \end{tabular}$

Najczęściej wykorzystywane w toku analiz statystycznych są macierze wag standaryzowane rzędami do jedynki. Standaryzacja rzędami do jedynki oznacza, że każda waga jest podzielona przez sumę wiersza (sumę wag wszystkich sąsiednich elementów). W rezultacie uzyskane wagi znajdą się w przedziale od 0 do 1. Wpływ obiektów z różną liczbą sąsiadów, w analizach bazujących na tak zestandaryzowanej macierzy wag, jest zrównoważony.

$\begin{tabular}{|c|c|c|c|c|c|c|c|c|}\hline \textbf{nr} &\textbf{1} &\textbf{2} &\textbf{3} &\textbf{4} &\textbf{5} &\textbf{6} &\textbf{7} &\textbf{8}\\\hline \textbf{1} &0 &$1/3$ &$1/3$ &$1/3$ &0 &0 &0 &0\\\hline \textbf{2} &$1/4$ &0 &$1/4$ &0 &0 &$1/4$ &$1/4$ &0\\\hline \textbf{3} &$1/5$ &$1/5$ &0 &$1/5$ &$1/5$ &$1/5$ &0 &0\\\hline \textbf{4} &$1/3$ &0 &$1/3$ &0 &$1/3$ &0 &0 &0\\\hline \textbf{5} &0 &0 &$1/5$ &$1/5$ &0 &$1/5$ &1/5 &$1/5$\\\hline \textbf{6} &0 &$1/5$ &$1/5$ &0 &$1/5$ &0 &$1/5$ &$1/5$\\\hline \textbf{7} &0 &$1/4$ &0 &0 &1/4$ &$1/4$ &0 &$1/4$\\\hline \textbf{8} &0 &0 &0 &0 &$1/3$ &$1/3$ &$1/3$ &0 \\\hline \end{tabular}$

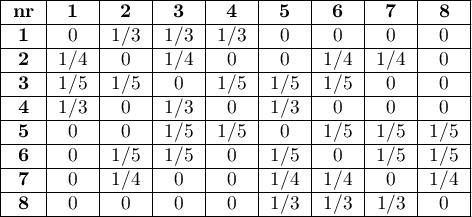
Wybrane macierze wag powinny odzwierciedlać zależności przestrzenne łączące analizowane obiekty. Im model wzajemnego oddziaływania obiektów w przestrzeni odzwierciedlony zostanie bardziej realistycznie, tym dokładniejsze wyniki uzyskamy.

Okno z ustawieniami opcji macierzy wag wywołujemy poprzez menu Analiza przestrzenna → Narzędzia → Macierz wag przestrzennych.

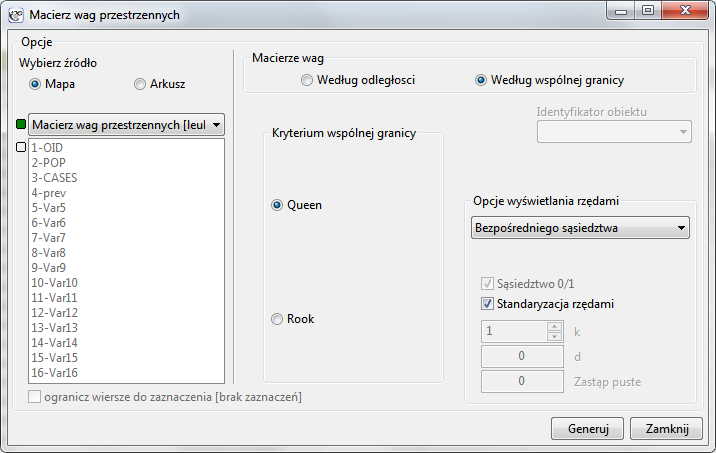
Macierz wag według odległości

Do wyznaczenia macierzy wag bazującej na odległościach punktów, powinniśmy dysponować danymi mapy zawierającej obiekty typu punkt, wielopunkt lub wielokąt. W przypadku analizy wielokątów obliczenia oparte są na centroidach, a przypadku wielopunktów na centrach obiektów.

Opis macierzy, której elementy powstają na zasadzie wyliczania odległości pomiędzy punktami można znaleźć w Podręczniku użytkownika - PQStat, w rozdziale dotyczącym macierzy podobieństwa.

2014/08/18 21:53 · admin

Macierz wag według wspólnej granicy

Do wyznaczenia macierzy wag bazującej na przyległości obiektów (wspólnej granicy), powinniśmy dysponować danymi mapy zawierającej obiekty typu wielopunkt lub wielokąt.

Kryterium wspólnej granicy

Wspólna granica porównywanych obiektów zwyczajowo rozumiana jest jako wspólny odcinek o niezerowej długości (tzn. odcinek dłuższy niż 1 punkt) – jest to sąsiedztwo typu Rook, lub jako dowolny odcinek (również o zerowej długości, czyli punkt) – jest to sąsiedztwo typu Queen.

Rodzaje macierzy wag bazujących na wspólnej granicy:

Macierz bezpośredniego sąsiedztwa – to symetryczna macierz kwadratowa, w której na głównej przekątnej znajdują się zera, elementy poza przekątną to:
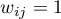- $w_{ij} = 1$ -– jeśli obiekty łączy wspólna granica,
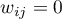- $w_{ij} = 0$ –- w przeciwnym przypadku.
Macierz sąsiedztwa (do k-tego stopnia) –- to symetryczna macierz kwadratowa, w której na głównej przekątnej znajdują się zera, elementy poza przekątną to:
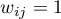- $w_{ij} = 1$ –- jeśli obiekty są bezpośrednimi sąsiadami (łączy je wspólna granica),
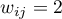- $w_{ij} = 2$ –- jeśli obiekty są sąsiadami drugiego stopnia (druga warstwa sąsiedztwa czyli tzw. sąsiad sąsiada)
- …
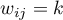- $w_{ij} = k$ –- jeśli obiekty są sąsiadami $k$ -tego stopnia ( $k$ -ta warstwa sąsiedztwa)
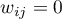- $w_{ij} = 0$ –- sąsiedztwo jest dalsze niż $k$ -tego stopnia.
Macierz sąsiedztwa (k-tego stopnia) –- to symetryczna macierz kwadratowa, w której na głównej przekątnej znajdują się zera, elementy poza przekątną to:
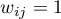- $w_{ij} = 1$ –- jeśli obiekty są sąsiadami $k$ -tego stopnia ( $k$ -ta warstwa sąsiedztwa)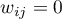
- $w_{ij} = 0$ –- w przeciwnym przypadku.