Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:wielowympl:logisporpl
Porównywanie modeli regresji logistycznej
Okno z ustawieniami opcji porównywania modeli wywołujemy poprzez menu Statystyka zaawansowana→Modele wielowymiarowe→Regresja logistyczna - porównywanie modeli
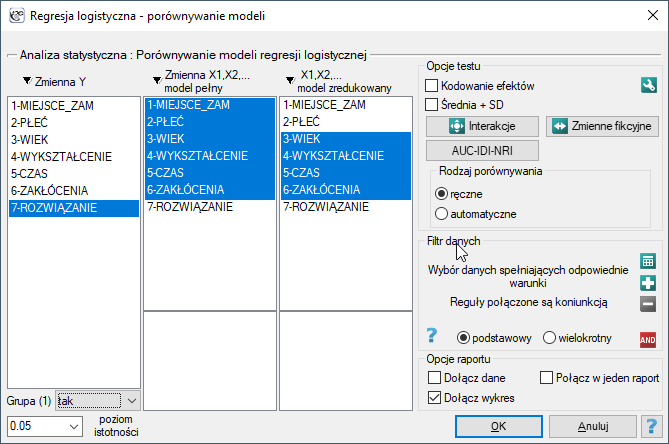
 Ze względu na możliwość jednoczesnej analizy wielu zmiennych niezależnych w jednym modelu regresji logistycznej, podobnie jak w liniowej regresji wielorakiej, istnieje problem wyboru optymalnego modelu. Wybierając zmienne niezależne należy pamiętać, by w modelu znajdowały się zmienne silnie skorelowane ze zmienną zależną i słabo skorelowane między sobą.
Ze względu na możliwość jednoczesnej analizy wielu zmiennych niezależnych w jednym modelu regresji logistycznej, podobnie jak w liniowej regresji wielorakiej, istnieje problem wyboru optymalnego modelu. Wybierając zmienne niezależne należy pamiętać, by w modelu znajdowały się zmienne silnie skorelowane ze zmienną zależną i słabo skorelowane między sobą.
Porównując modele z różną liczbą zmiennych niezależnych zwracamy uwagę na dopasowanie modelu oraz kryteria informacyjne. Dla każdego modelu wyliczamy również maksimum funkcji wiarygodności, które następnie porównujemy przy użyciu testu ilorazu wiarygodności.
Hipotezy:
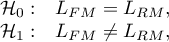
gdzie:
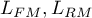 - maksimum funkcji wiarygodności w porównywanych modelach (pełnym i zredukowanym).
- maksimum funkcji wiarygodności w porównywanych modelach (pełnym i zredukowanym).
Statystyka testowa ma postać:
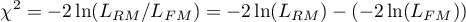
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 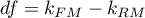 stopniami swobody, gdzie
stopniami swobody, gdzie 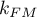 i
i 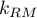 to ilość szacowanych parametrów w porównywanych modelach.
to ilość szacowanych parametrów w porównywanych modelach.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Decyzję o tym, który model wybrać podejmujemy na podstawie wielkości 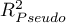 ,
, 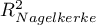 ,
, 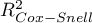 oraz wyniku testu ilorazu wiarygodności porównującego kolejno powstające (sąsiednie) modele. Jeśli porównywane modele nie różnią się istotnie, to powinniśmy wybrać ten z mniejszą liczbą zmiennych. Brak różnicy oznacza bowiem, że zmienne, które są w modelu pełnym, a nie ma ich w modelu zredukowanym, nie wnoszą istotnej informacji. Jeśli natomiast różnica jest istotna statystycznie oznacza to, że jeden z nich (ten z większą liczbą zmiennych, o większym
oraz wyniku testu ilorazu wiarygodności porównującego kolejno powstające (sąsiednie) modele. Jeśli porównywane modele nie różnią się istotnie, to powinniśmy wybrać ten z mniejszą liczbą zmiennych. Brak różnicy oznacza bowiem, że zmienne, które są w modelu pełnym, a nie ma ich w modelu zredukowanym, nie wnoszą istotnej informacji. Jeśli natomiast różnica jest istotna statystycznie oznacza to, że jeden z nich (ten z większą liczbą zmiennych, o większym  i mniejszej wartości kryterium informacyjnego AIC, AICc lub BIC) jest istotnie lepszy niż drugi.
i mniejszej wartości kryterium informacyjnego AIC, AICc lub BIC) jest istotnie lepszy niż drugi.
Porównanie wartości prognostycznej modeli.
Budowane modele regresji pozwalają przewidzieć prawdopodobieństwo wystąpienia badanego zdarzenia w oparciu o analizowane zmienne niezależne. Gdy znanych jest już wiele zmiennych (czynników) zwiększających ryzyko wystąpienia zdarzenia, wówczas ważnym kryterium dla nowego kandydata na czynnik ryzyka jest poprawa skuteczności predykcji po dołączeniu tego czynnika do modelu.
Dla ustalenia uwagi posłużmy się przykładem. Załóżmy, że badamy czynniki ryzyka wystąpienia choroby wieńcowej. Do znanych czynników ryzyka tej choroby należą wiek, wartości ciśnienia skurczowego i rozkurczowego, otyłość, cholesterol czy też palenie. Badacze są jednak zainteresowani jak bardzo włączenie poszczególnych czynników do modelu regresji pozwoli na znaczną poprawę oszacowywania ryzyka wystąpienia choroby. Czynniki ryzyka dołączone do modelu będą miały znaczenie prognostyczne, jeśli nowy i większy model (zawierający te czynniki) będzie wykazywał lepszą wartość prognostyczną niż model ich pozbawiony.
Wartość prognostyczna modelu wynika z wyznaczonej wartości przewidywanego prawdopodobieństwa wystąpienia zdarzenia, w tym przypadku choroby wieńcowej. Wartość ta jest wyznaczana na podstawie modelu dla każdej badanej osoby. Im bliższe wartości 1 jest przewidywane prawdopodobieństwo, tym bardziej prawdopodobna jest choroba. Na bazie prawdopodobieństwa przewidywanego można wyznaczyć i porównać pomiędzy różnymi modelami wartość pola AUC pod krzywą ROC a także współczynnik  i
i 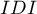 .
.
- Zmiana pola pod krzywą ROC
Krzywa ROC w modelach regresji logistycznej zbudowana jest w oparciu o klasyfikację przypadków do grupy doświadczającej zdarzenia lub nie, oraz przewidywane prawdopodobieństwo zmiennej zależnej 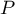 . Czym większe pole pod krzywą, tym trafniej prawdopodobieństwo wyznaczone przez model przewiduje rzeczywiste wystąpienie zdarzenia. Jeśli porównujemy modele zbudowane w oparciu o większą lub mniejszą liczbę czynników prognostycznych, to porównując wielkość pola pod krzywą możemy sprawdzić, czy dołożenie czynników poprawiło znacząco predykcję modelu.
. Czym większe pole pod krzywą, tym trafniej prawdopodobieństwo wyznaczone przez model przewiduje rzeczywiste wystąpienie zdarzenia. Jeśli porównujemy modele zbudowane w oparciu o większą lub mniejszą liczbę czynników prognostycznych, to porównując wielkość pola pod krzywą możemy sprawdzić, czy dołożenie czynników poprawiło znacząco predykcję modelu.
Hipotezy:
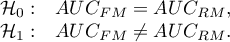
Sposób wyznaczania staystyki testowej oparty o metodę DeLonga, został opisany w rozdziale Porównywanie krzywych ROC.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

- Poprawa reklasyfikacji netto
Miara ta oznaczana jest skrótem  (ang. Net Reclassification Improvement).
(ang. Net Reclassification Improvement).  skupia się na tabeli reklasyfikacji opisującej przesunięcie wartości prawdopodobieństwa w górę lub w dół po dołożeniu nowego czynnika do modelu. Wyznacza się go na bazie dwóch oddzielnych współczynników, tzn. współczynnika wyznaczonego oddzielnie dla obiektów doświadczających zdarzenia (1) i oddzielnie dla tych niedoświadczających zdarzenia (0).
skupia się na tabeli reklasyfikacji opisującej przesunięcie wartości prawdopodobieństwa w górę lub w dół po dołożeniu nowego czynnika do modelu. Wyznacza się go na bazie dwóch oddzielnych współczynników, tzn. współczynnika wyznaczonego oddzielnie dla obiektów doświadczających zdarzenia (1) i oddzielnie dla tych niedoświadczających zdarzenia (0).  może być wyznaczany przy zadanym podziale prawdopodobieństwa przewidywanego na kategorie (
może być wyznaczany przy zadanym podziale prawdopodobieństwa przewidywanego na kategorie ( kategorialny) lub bez konieczności wyznaczania kategorii (
kategorialny) lub bez konieczności wyznaczania kategorii ( ciągły).
ciągły).
- NRI kategorialny wymaga arbitralnego wyznaczenia podziału wartości prawdopodobieństwa przewidywanego z modelu. Podanych punktów podziału może być maksymalnie 9, a więc przewidywanych kategorii maksymalnie 10. Najczęściej jednak stosuje się jeden lub dwa punkty podziałowe. Przy czym należy zauważyć, że wartości kategorialnego
 mogą być z sobą porównywane tylko wtedy, jeśli bazowały na tych samych punktach podziału. Dla zobrazowania sytuacji ustalmy dwa przykładowe punkty podziału prawdopodobieństwa: 0.1 i 0.3. Jeśli badana osoba w modelu „starym” (mniejszym) uzyskała prawdopodobieństwo poniżej 0.1, a w „nowym modelu” (zwiększonym o nowy potencjalny czynnik ryzyka) prawdopodobieństwo znajdujące się pomiędzy 0.1 a 0.3, to znaczy, że osoba ta została reklasyfikowana w górę (tabela, sytuacja 1). Jeśli wartość prawdopodobieństwa z obu modeli mieści się w tym samym przedziale, wówczas osoba nie została reklasyfikowana (tabela, sytuacja 2), natomiast jeśli prawdopodobieństwo z modelu „nowego” będzie niższe niż w modelu „starym”, oznacza to reklasyfikację w dół badanej osoby (tabela, sytuacja 3).
mogą być z sobą porównywane tylko wtedy, jeśli bazowały na tych samych punktach podziału. Dla zobrazowania sytuacji ustalmy dwa przykładowe punkty podziału prawdopodobieństwa: 0.1 i 0.3. Jeśli badana osoba w modelu „starym” (mniejszym) uzyskała prawdopodobieństwo poniżej 0.1, a w „nowym modelu” (zwiększonym o nowy potencjalny czynnik ryzyka) prawdopodobieństwo znajdujące się pomiędzy 0.1 a 0.3, to znaczy, że osoba ta została reklasyfikowana w górę (tabela, sytuacja 1). Jeśli wartość prawdopodobieństwa z obu modeli mieści się w tym samym przedziale, wówczas osoba nie została reklasyfikowana (tabela, sytuacja 2), natomiast jeśli prawdopodobieństwo z modelu „nowego” będzie niższe niż w modelu „starym”, oznacza to reklasyfikację w dół badanej osoby (tabela, sytuacja 3).
![LaTeX \begin{tabular}{|c|c|c||c|c||c|c|}
\hline
modele regresji&\multicolumn{2}{|c||}{sytuacja 1}&\multicolumn{2}{|c||}{sytuacja 2}&\multicolumn{2}{|c|}{sytuacja 3}\\\hline
prawdop. przewidywane&"stary"&"nowy"&"stary"&"nowy"&"stary"&"nowy"\\\hline
[0.3 do 1]&&&&&$\oplus$&\\\hline
[0.1; 0.3)&&$\oplus$&$\oplus$&$\oplus$&&$\oplus$\\\hline
[0; 0.1)&$\oplus$&&&&&\\\hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img2625dcf065b9f89d09a26cab3972ac0f.png)
- NRI ciągły nie wymaga arbitralnego wyznaczenia kategorii, ponieważ każda, nawet najmniejsza zmiana prawdopodobieństwa w górę lub w dół w stosunku do prawdopodobieństwa wyznaczonego w „starym modelu”, traktowana jest jako przejście do kolejnej kategorii. Kategorii jest więc nieskończenie wiele, tak jak wiele jest możliwych zmian.
Uwaga!
Stosowanie  ciągłego nie wymaga arbitralnego definiowania punktów podziału prawdopodobieństwa, jednak nawet niewielkie zmiany ryzyka (nie mające odzwierciedlenia w klinicznych obserwacjach) mogą wpływać na zwiększenie lub zmniejszenie tego współczynnika. Kategorialny współczynnik
ciągłego nie wymaga arbitralnego definiowania punktów podziału prawdopodobieństwa, jednak nawet niewielkie zmiany ryzyka (nie mające odzwierciedlenia w klinicznych obserwacjach) mogą wpływać na zwiększenie lub zmniejszenie tego współczynnika. Kategorialny współczynnik  pozwala na odzwierciedlenie tylko ważnych dla badacza zmian polegających na przekroczeniu zadanych wartości ryzyka wystąpienia zdarzenia (wartości prawdopodobieństwa przewidywanego).
pozwala na odzwierciedlenie tylko ważnych dla badacza zmian polegających na przekroczeniu zadanych wartości ryzyka wystąpienia zdarzenia (wartości prawdopodobieństwa przewidywanego).
By wyznaczyć  definiujemy:
definiujemy:
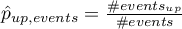
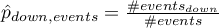
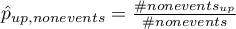
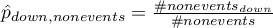
gdzie:
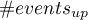 - liczba obiektów z grupy doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w górę,
- liczba obiektów z grupy doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w górę,
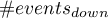 - liczba obiektów z grupy doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w dół,
- liczba obiektów z grupy doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w dół,
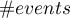 - liczba obiektów w grupie doświadczającej zdarzenia,
- liczba obiektów w grupie doświadczającej zdarzenia,
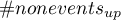 - liczba obiektów z grupy nie doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w górę,
- liczba obiektów z grupy nie doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w górę,
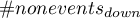 - liczba obiektów z grupy nie doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w dół,
- liczba obiektów z grupy nie doświadczającej zdarzenia, u których nastąpiła zmiana prawdopodobieństwa przewidywanego o przynajmniej jedną kategorię w dół,
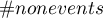 - liczba obiektów w grupie nie doświadczającej zdarzenia.
- liczba obiektów w grupie nie doświadczającej zdarzenia.
Ogólny współczynnik  oraz współczynniki wyrażające procentową zmianę klasyfikacji jest wyznaczany z wzoru:
oraz współczynniki wyrażające procentową zmianę klasyfikacji jest wyznaczany z wzoru:
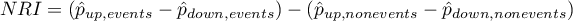
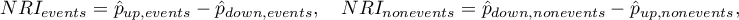
Współczynnik 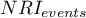 może być interpretowany jako procent netto prawidłowo reklasyfikowanych osób, u których wystąpiło zdarzenie, a
może być interpretowany jako procent netto prawidłowo reklasyfikowanych osób, u których wystąpiło zdarzenie, a 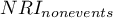 jako procent netto prawidłowo reklasyfikowanych osób, u których nie wystąpiło zdarzenie. Ogólny współczynnik
jako procent netto prawidłowo reklasyfikowanych osób, u których nie wystąpiło zdarzenie. Ogólny współczynnik  jest wyrażony jako suma współczynników
jest wyrażony jako suma współczynników 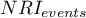 i
i 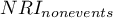 , przez co jest współczynnikiem domyślnie ważonym przez częstość zdarzenia i nie może być interpretowany jako procent.
, przez co jest współczynnikiem domyślnie ważonym przez częstość zdarzenia i nie może być interpretowany jako procent.
Współczynniki 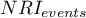 należą do przedziału od -1 do 1 (od -100% do 100%), a ogólny współczynniki
należą do przedziału od -1 do 1 (od -100% do 100%), a ogólny współczynniki  do przedziału od -2 do 2. Wartości dodatnie współczynników świadczą o korzystnej reklasyfikacji, a ujemne o niekorzystnej reklasyfikacji na skutek dołożenia nowej zmiennej do modelu.
do przedziału od -2 do 2. Wartości dodatnie współczynników świadczą o korzystnej reklasyfikacji, a ujemne o niekorzystnej reklasyfikacji na skutek dołożenia nowej zmiennej do modelu.
Test Z do sprawdzania istotności współczynnika NRI
Przy pomocy tego testu badamy czy zmiana klasyfikacji wyrażona współczynnikiem  była istotna.
była istotna.
Hipotezy:
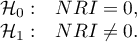
Statystyka testowa ma postać:
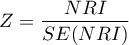
gdzie:
![LaTeX $
\begin{array}{cl}
SE(NRI)= & [\left(\frac{\#events_{up} + \#events_{down}}{\#events^2}-\frac{(\#events_{up} + \#events_{down})^2}{\#events^3}\right)+\\
& +\left(\frac{\#nonevents_{down} + \#nonevents_{up}}{\#nonevents^2}-\frac{(\#nonevents_{down} + \#nonevents_{up})^2}{\#nonevents^3}\right)]^{1/2}
\end{array}
$](/lib/exe/fetch.php?media=wiki:latex:/img4a0d14005d06df04a67c84ba7e8733d7.png)
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

- Zintegrowana poprawa dyskryminacji
Miara ta oznaczana jest skrótem 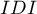 (ang. Integrated Discrimination Improvement). Współczynniki
(ang. Integrated Discrimination Improvement). Współczynniki 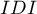 poskazuje różnicę pomiędzy wartością średniej zmiany prawdopodobieństwa przewidywanego pomiędzy grupą obiektów doświadczających zdarzenia a grupą obiektów, które zdarzenia nie doświadczyły.
poskazuje różnicę pomiędzy wartością średniej zmiany prawdopodobieństwa przewidywanego pomiędzy grupą obiektów doświadczających zdarzenia a grupą obiektów, które zdarzenia nie doświadczyły.
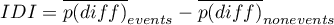
gdzie:
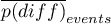 - średnia różnicy wartości prawdopodobieństwa przewidywanego między modelami regresji („starym” i „nowym”) dla obiektów, które doświadczyły zdarzenia,
- średnia różnicy wartości prawdopodobieństwa przewidywanego między modelami regresji („starym” i „nowym”) dla obiektów, które doświadczyły zdarzenia,
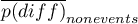 - średnia różnicy wartości prawdopodobieństwa przewidywanego między modelami regresji („starym” i „nowym”) dla obiektów, które nie doświadczyły zdarzenia.
- średnia różnicy wartości prawdopodobieństwa przewidywanego między modelami regresji („starym” i „nowym”) dla obiektów, które nie doświadczyły zdarzenia.
Test Z do sprawdzania istotności współczynnika IDI
Przy pomocy tego testu badamy czy różnica pomiędzy wartością średniej zmiany prawdopodobieństwa przewidywanego pomiędzy grupą obiektów doświadczających zdarzenia a obiektami nie doświadczającymi zdarzenia, wyrażona współczynnikiem 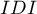 , była istotna.
, była istotna.
Hipotezy:
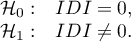
Statystyka testowa ma postać:
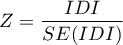
gdzie:
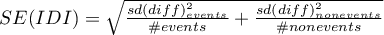
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

W programie PQStat porównywanie modeli możemy przeprowadzić ręcznie lub automatycznie.
Ręczne porównywanie modeli - polega na zbudowaniu 2 modeli:
pełnego - modelu z większą liczbą zmiennych,
zredukowanego - modelu z mniejszą liczbą zmiennych - model taki powstaje z modelu pełnego po usunięciu zmiennych, które z punktu widzenia badanego zjawiska są zbędne.
Wybór zmiennych niezależnych w porównywanych modelach a następnie wybór lepszego modelu, na podstawie uzyskanych wyników porównania, należy do badacza.
Automatyczne porównywanie modeli jest wykonywane w kilku krokach:
[krok 1] Zbudowanie modelu z wszystkich zmiennych.
[krok 2] Usunięcie jednej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.
[krok 3] Porównanie modelu pełnego i zredukowanego.
[krok 4] Usunięcie kolejnej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.
[krok 5] Porównanie modelu wcześniejszego i nowo zredukowanego.
[…]
W ten sposób powstaje wiele, coraz mniejszych modeli. Ostatni model zawiera tylko 1 zmienną niezależną.
Przykład c.d. (plik zadanie.pqs)
W eksperymencie badającym umiejętność koncentracji, dla 130 osób zbioru uczącego, zbudowano model regresji logistycznej w oparciu o następujące zmienne:
zmienna zależna: ROZWIĄZANIE (tak/nie) - informacja o tym, czy zadanie zostało rozwiązane poprawnie czy też nie;
zmienne niezależne:
MIEJSCEZAM (1=miasto/0=wieś),
PŁEĆ (1=kobieta/0=mężczyzna),
WIEK (w latach),
WYKSZTAŁCENIE (1=podstawowe, 2=zawodowe, 3=średnie, 4=wyższe),
CZAS rozwiązywania (w minutach),
ZAKŁÓCENIA (1=tak/0=nie).
Sprawdzimy, czy wszystkie zmienne niezależne są w modelu niezbędne.
- Ręczne porównywanie modeli.
Na podstawie zbudowanego wcześniej modelu pełnego możemy podejrzewać, że zmienne: MIEJSCEZAM i PŁEĆ mają niewielki wpływ na budowany model (tzn. na podstawie tych zmiennych nie możemy z sukcesem dokonywać klasyfikacji). Sprawdzimy czy, ze statystycznego punktu widzenia, model pełny jest lepszy niż model po usunięciu tych dwóch zmiennych.
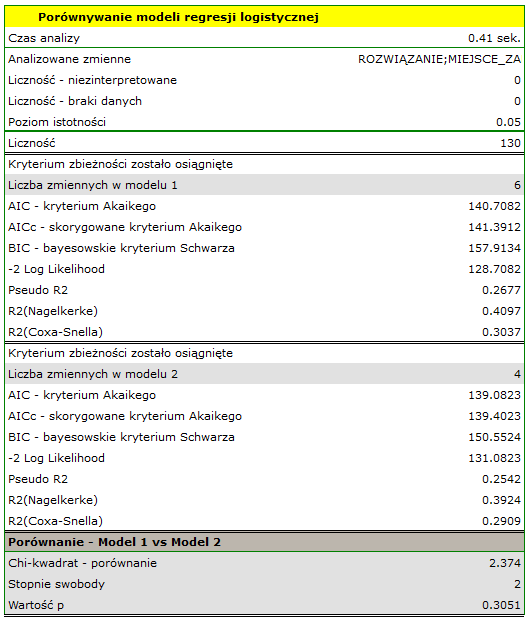
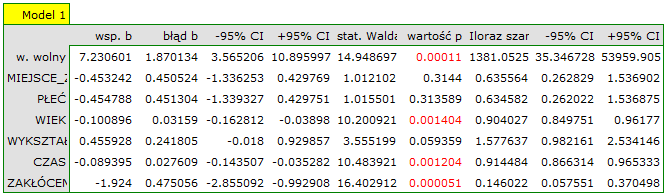
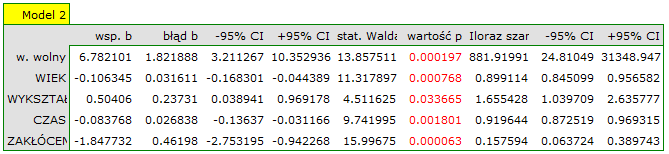
Wynik testu ilorazu wiarygodności (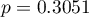 ) wskazuje , że nie ma podstaw by uważać, że model pełny jest lepszy niż model zredukowany. Zatem, przy nieznacznej utracie jakości modelu, miejsce zamieszkania i płeć mogą zostać pominięte.
) wskazuje , że nie ma podstaw by uważać, że model pełny jest lepszy niż model zredukowany. Zatem, przy nieznacznej utracie jakości modelu, miejsce zamieszkania i płeć mogą zostać pominięte.
Porównania obu modeli pod względem zdolności do klasyfikacji możemy dokonać porównując krzywe ROC dla tych modeli, wartość NRI i IDI. W tym celu wybieramy odpowiednią opcję w oknie analizy. Uzyskany raport, podobnie jak wcześniejszy, wskazuje, że modele nie różnią się jakością predykcji tzn. wartości p dla porównania krzywych ROC oraz do oceny wskaźników NRI i IDI są nieistotne statystycznie. Decydujemy zatem pominąć płeć i miejsce zamieszkania w ostatecznym modelu.

- Automatyczne porównywanie modeli.
W przypadku automatycznego porównywania modeli uzyskaliśmy bardzo podobne wyniki. Najlepszym modelem jest model zbudowany na podstawie zmiennych niezależnych: WIEK, WYKSZTAŁCENIE, CZAS rozwiązywania, ZAKŁUCENIA.
Na podstawie powyższych analiz, ze statystycznego punktu widzenia, optymalnym modelem jest model zawierający 4 najważniejsze zmienne niezależne: WIEK, WYKSZTAŁCENIE, CZAS rozwiązywania, ZAKŁUCENIA. Dokładną jego analizę możemy przeprowadzić w module Regresja Logistyczna. Jednak ostateczna decyzja, który model wybrać należy do eksperymentatora.
Badano czynniki ryzyka pewnej choroby serca takie jak wiek, bmi, palenie, cholesterol we frakcji LDL, cholesterol we frakcji HDL i nadciśnienie. Z punktu widzenia badacza interesujące było określenie jak bardzo informacja o paleniu może poprawić predykcję występowania badanej choroby.
Porównujemy model regresji logistycznej opisujący ryzyko choroby serca na podstawie wszystkich badanych zmiennych z modelem pozbawionym informacji o paleniu. W oknie analizy zaznaczamy opcje związane z oceną predykcji, czyli krzywą ROC oraz współczynniki NRI. Dodatkowo wskazujemy, by w raporcie znalazły się wszystkie proponowane wykresy.

Analiza raportu wskazuje na ważne różnice w predykcji na skutek dodania do modelu informacji o paleniu, chociaż nie są one istotne w opisie krzywej ROC (p=0.057).
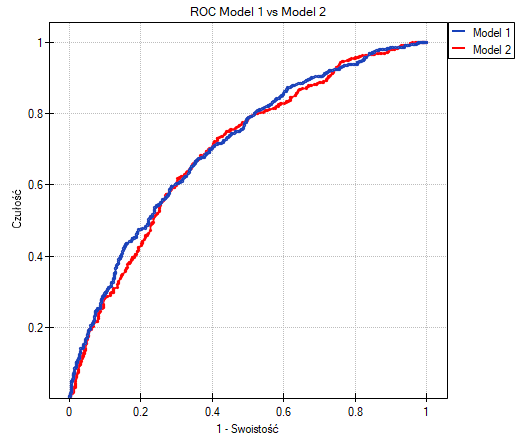
Ciągłe wartości współczynnika IDI i NRI wskazują na istotną statystycznie i korzystą zmianę (wartości tych współczynników są dodatnie, a wartości p<0.05). Prognoza dla osób z chorobą serca poprawiła się o ponad 5% a osób bez tej choroby o ponad 13% (NRI(chory)=0.0522, NRI(zdrowy)=0.1333)) na skutek uwzględnienia informacji o paleniu.
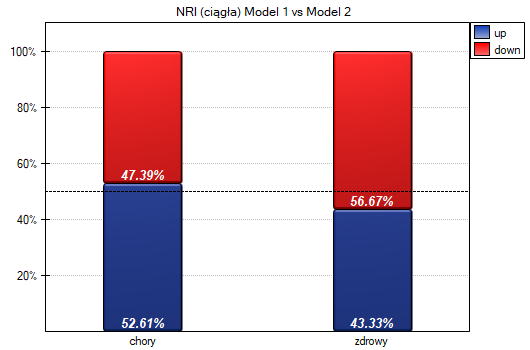
Wnioski wyciągnięte na bazie NRI widzimy również na wykresie. Wzrost prognozowanego przez model prawdopodobieństwa choroby widzimy u osób chorych (więcej osób zostało przeklasyfikowanych w górę niż w dół 52.61% vs 47.39%) natomiast spadek prawdopodobieństwa dotyczy w większym stopniu osób zdrowych (więcej osób zostało przeklasyfikowanych w dół niż w górę 56.67% vs 43.33%).
Istnieje też możliwość wyznaczenia NRI kategorialnego, ale w tym celu należałoby najpierw ustalić przyjęte w literaturze dotyczącej chorób serca punkty odcięcia prawdopodobieństwa wyznaczonego przez model.
statpqpl/wielowympl/logisporpl.txt · ostatnio zmienione: 2022/11/19 18:32 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

