Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Analiza przeżycia » Podstawy analizy przeżycia » Krzywe Kaplana-Meiera
Pasek boczny
statpqpl:survpl:wsteppl:kmpl
Krzywe Kaplana-Meiera
 Krzywe Kaplana-Meiera pozwalają na ocenę czasu przeżycia bez konieczności arbitralnego grupowania obserwacji, tak jak to jest w tabelach przeżycia. Estymator ten został wprowadzony przez Kaplana i Meiera (1958)1).
Krzywe Kaplana-Meiera pozwalają na ocenę czasu przeżycia bez konieczności arbitralnego grupowania obserwacji, tak jak to jest w tabelach przeżycia. Estymator ten został wprowadzony przez Kaplana i Meiera (1958)1).
Okno z ustawieniami opcji krzywej Kaplana-Meiera wywołujemy poprzez menu Statystyka→Analiza przeżycia→Analiza Kaplana-Meiera
Podobnie jak dla tablic przeżycia, wyliczamy tutaj funkcję przeżycia, czyli prawdopodobieństwo przeżycia do danego czasu. Wykres funkcji przeżycia Kaplana-Meiera tworzy funkcja schodkowa. Na podstawie błędu standardowego (formuła Greenwooda) i transformacji logarytmicznej (log-log) zbudowane są przedziały ufności wokół tej krzywej. Punkt czasu, przy którym wartość funkcji przyjmuje 0.5, to mediana czasu przeżycia. Mediana ta wskazuje na 50% ryzyko wystąpienia zgonu, czyli przewiduje iż u połowy pacjentów nastąpi zgon w ciągu wskazanego czasu. Zarówno mediana jak i inne percentyle wyznaczane są jako najkrótszy czas przeżycia, dla którego funkcja przeżycia jest mniejsza lub równa danemu percentylowi. Dla mediany wyznaczany jest przedział ufności w oparciu o metodę test-based autorstwa Brookmeyer i Crowley (1982)2). Średnia czasu przeżycia jest wyznaczona jako pole pod krzywą przeżycia.
Dane dotyczące czasu przeżycia są zwykle mocno skośne, dlatego w analizie przeżycia, mediana jest lepszą miarą tendencji centralnej niż średnia.
Przykład c.d. (plik przeszczep.pqs)
Przedstawimy długość życia po przeszczepie wątroby przy pomocy krzywej Kaplana-Meiera
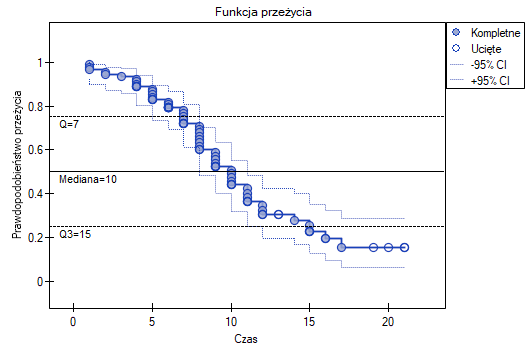

Funkcja przeżycia nie opada gwałtownie zaraz po przeszczepie. Wnioskujemy stąd, że początkowy okres po transplantacji nie jest szczególnie obarczony ryzykiem zgonu. Z wartości mediany wynika, że w ciągu 10 lat od przeszczepu oczekujemy, że u połowy pacjentów nastąpi zgon. Wartość tę zaznaczamy na wykresie rysując linię w punkcie 0.5 oznaczającym medianę. W podobny sposób zaznaczamy na wykresie kwartyle.
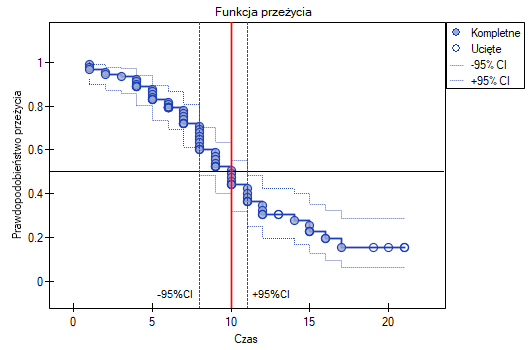
Przedział ufności dla mediany możemy zobrazować na wykresie wyrysowując linie pionowe w oparciu o przedział ufności wokół krzywej oraz linie na poziomie 0.5.
statpqpl/survpl/wsteppl/kmpl.txt · ostatnio zmienione: 2023/10/27 21:47 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

