Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Analiza przeżycia » Podstawy analizy przeżycia
Pasek boczny
statpqpl:survpl:wsteppl
Podstawy analizy przeżycia
Tabele przeżycia
Okno z ustawieniami opcji tabel trwania życia wywołujemy poprzez menu Statystyka→Analiza przeżycia→Tabele przeżycia
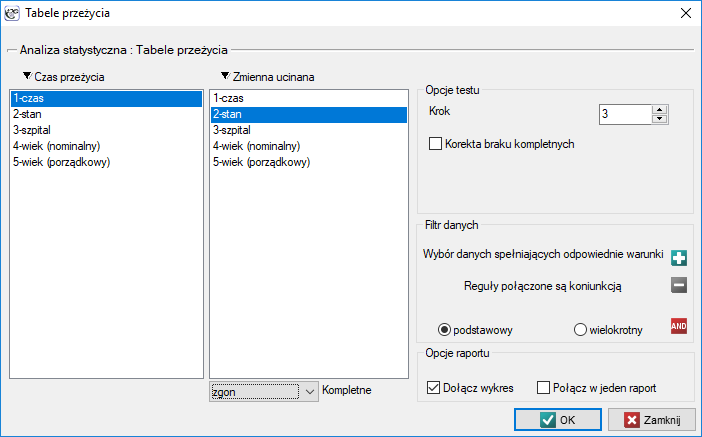
Tabele trwania życia tworzy się dla podanych przez badacza przedziałów czasu przeżycia o równej rozpiętości. Przedziały te można zdefiniować podając krok. Dla każdego przedziału program PQStat wylicza:
- liczbę przypadków wchodzących - liczba osób, które przeżyły do określonego przez przedział czasu;
- liczbę przypadków uciętych - liczba osób w danym przedziale, które są zdefiniowane jako przypadki ucięte;
- liczbę przypadków zagrożonych - liczba przypadków, które wchodzą do danego przedziału minus połowa liczby przypadków uciętych w danym przedziale;
- liczbę przypadków kompletnych - liczba osób, które doświadczyły zdarzenia (czyli zmarły) w danym przedziale;
- proporcje przypadków kompletnych - stosunek liczby przypadków kompletnych (zgonów) w danym przedziale do liczby przypadków zagrożonych w tym przedziale;
- proporcje przypadków przeżywających - oblicza się jako 1 minus proporcja przypadków kompletnych w danym przedziale;
- skumulowane proporcje przeżywających (funkcja przeżycia) - prawdopodobieństwo przeżycia do danego czasu
 ponieważ żeby przeżyć kolejny przedział czasu, trzeba przeżyć wszystkie poprzednie, to prawdopodobieństwo to wyliczane jest jako iloczyn wszystkich poprzednich proporcji przypadków przeżywających;
ponieważ żeby przeżyć kolejny przedział czasu, trzeba przeżyć wszystkie poprzednie, to prawdopodobieństwo to wyliczane jest jako iloczyn wszystkich poprzednich proporcji przypadków przeżywających;
 błąd standardowy funkcji przeżycia;
błąd standardowy funkcji przeżycia;
- gęstość prawdopodobieństwa - oszacowane prawdopodobieństwo doświadczenia zdarzenia (zgonu) w danym przedziale obliczone w jednostce czasu;
 błąd standardowy gęstości prawdopodobieństwa;
błąd standardowy gęstości prawdopodobieństwa;
- stopę hazardu - prawdopodobieństwo (wyliczane na jednostkę czasu) tego, że przypadek, który przeżył do początku danego przedziału doświadczy w tym przedziale zdarzenia (zgonu);
 błąd standardowy stopy hazardu.
błąd standardowy stopy hazardu.
Uwaga!
W przypadku braku obserwacji kompletnych w dowolnym przedziale czasu przeżycia istnieje możliwość zastosowania korekty. Zerową liczbę przypadków kompletnych zastępuje się wówczas wartością 0.5.
Interpretacja graficzna
Dla zobrazowania informacji uzyskanych dzięki tabelom przeżycia możemy posłużyć się kilkoma wykresami:
- wykresem funkcji przeżycia,
- wykresem gęstości prawdopodobieństwa,
- wykresem stopy hazardu.
Przykład (plik przeszczep.pqs)
Badano długość życia chorych po przeszczepie wątroby. Przez okres 21 lat poddano obserwacji grupę 89 pacjentów, których wiek w chwili przeszczepu należał do przedziału 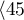 lat
lat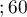 lat
lat . Fragment zebranych danych przedstawia poniższa tabela:
. Fragment zebranych danych przedstawia poniższa tabela:
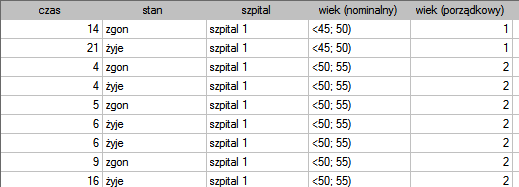
Dane kompletne w tej analizie to te, o których mamy pełną informację o długości życia po przeszczepie, czyli opisane jako „zgon” (są to 53 osoby, co stanowi 59.55%). Dane ucięte to te, o których tej informacji nie mamy ponieważ w chwili zakończenia badania żyją (jest to 36 osób, co stanowi 40.45%). Budujemy tablice trwania życia tych pacjentów tworząc 3 letnie przedziały czasowe:
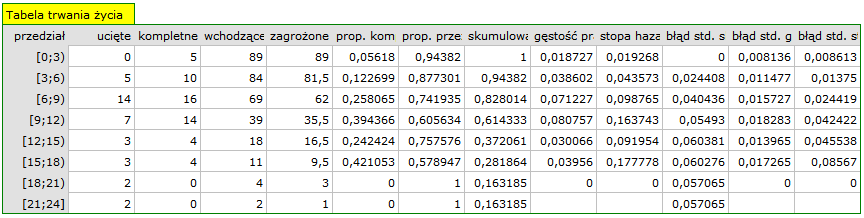
Dla każdego 3-letniego przedziału możemy zinterpretować uzyskane w tabeli wyniki - przykładowo dla osób, które żyją przynajmniej 9 lat od przeszczepu, a zatem weszły do przedziału [9;12):
- liczba osób, które przeżyły do 9 lat od przeszczepu to 39;
- jest 7 osób, o których wiemy, że żyły przynajmniej 9-12 lat - gdy informacje o nich były zbierane, ale nie wiemy czy żyły dłużej, gdyż po tym czasie wypadły z badania;
- liczbę osób zagrożonych zgonem w tym przedziale to 36;
- jest 14 osób, o których wiemy, że zmarły od 9 do 12 lat po przeszczepie;
- 39.4% narażonych pacjentów zmarło 9-12 lat po przeszczepie;
- 60.6% narażonych pacjentów żyło 9-12 lat po przeszczepie;
- procent przeżywających do 9 lat po przeszczepie to 61.4%
 5%
5% - 0.08
 0.02 - to prawdopodobieństwo zgonu dla każdego roku z przedziału 9-12
0.02 - to prawdopodobieństwo zgonu dla każdego roku z przedziału 9-12 - 0.16
 0.04 - to warunkowe, roczne prawdopodobieństwo zgonu dla przypadku, który przeżył do początku przedziału 9-12;
0.04 - to warunkowe, roczne prawdopodobieństwo zgonu dla przypadku, który przeżył do początku przedziału 9-12;
Wyniki przedstawimy na kilku wykresach:
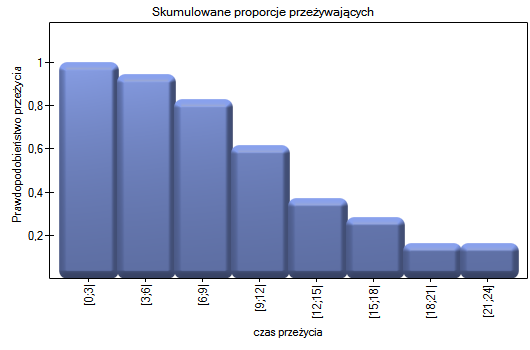
Prawdopodobieństwo przeżycia maleje wraz z upływem czasu jaki minął od przeszczepu. Nie obserwujemy jednak nagłego spadku funkcji przeżycia, a więc czasu w który gwałtownie wzrastałoby prawdopodobieństwo zgonu.
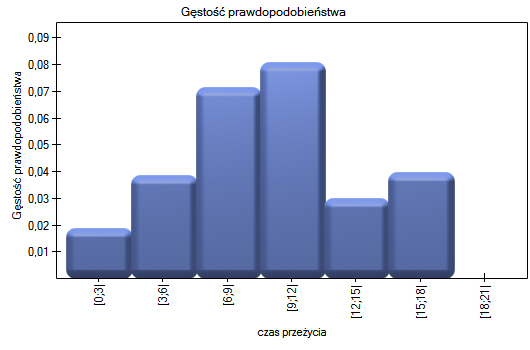
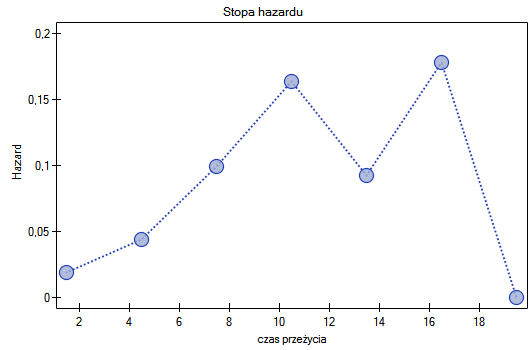
2014/08/24 23:44
· admin
Krzywe Kaplana-Meiera
 Krzywe Kaplana-Meiera pozwalają na ocenę czasu przeżycia bez konieczności arbitralnego grupowania obserwacji, tak jak to jest w tabelach przeżycia. Estymator ten został wprowadzony przez Kaplana i Meiera (1958)1).
Krzywe Kaplana-Meiera pozwalają na ocenę czasu przeżycia bez konieczności arbitralnego grupowania obserwacji, tak jak to jest w tabelach przeżycia. Estymator ten został wprowadzony przez Kaplana i Meiera (1958)1).
Okno z ustawieniami opcji krzywej Kaplana-Meiera wywołujemy poprzez menu Statystyka→Analiza przeżycia→Analiza Kaplana-Meiera
Podobnie jak dla tablic przeżycia, wyliczamy tutaj funkcję przeżycia, czyli prawdopodobieństwo przeżycia do danego czasu. Wykres funkcji przeżycia Kaplana-Meiera tworzy funkcja schodkowa. Na podstawie błędu standardowego (formuła Greenwooda) i transformacji logarytmicznej (log-log) zbudowane są przedziały ufności wokół tej krzywej. Punkt czasu, przy którym wartość funkcji przyjmuje 0.5, to mediana czasu przeżycia. Mediana ta wskazuje na 50% ryzyko wystąpienia zgonu, czyli przewiduje iż u połowy pacjentów nastąpi zgon w ciągu wskazanego czasu. Zarówno mediana jak i inne percentyle wyznaczane są jako najkrótszy czas przeżycia, dla którego funkcja przeżycia jest mniejsza lub równa danemu percentylowi. Dla mediany wyznaczany jest przedział ufności w oparciu o metodę test-based autorstwa Brookmeyer i Crowley (1982)2). Średnia czasu przeżycia jest wyznaczona jako pole pod krzywą przeżycia.
Dane dotyczące czasu przeżycia są zwykle mocno skośne, dlatego w analizie przeżycia, mediana jest lepszą miarą tendencji centralnej niż średnia.
Przykład c.d. (plik przeszczep.pqs)
Przedstawimy długość życia po przeszczepie wątroby przy pomocy krzywej Kaplana-Meiera
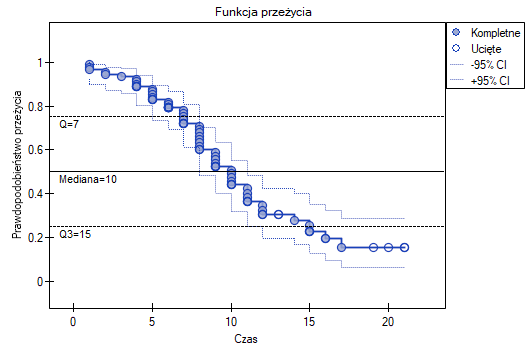

Funkcja przeżycia nie opada gwałtownie zaraz po przeszczepie. Wnioskujemy stąd, że początkowy okres po transplantacji nie jest szczególnie obarczony ryzykiem zgonu. Z wartości mediany wynika, że w ciągu 10 lat od przeszczepu oczekujemy, że u połowy pacjentów nastąpi zgon. Wartość tę zaznaczamy na wykresie rysując linię w punkcie 0.5 oznaczającym medianę. W podobny sposób zaznaczamy na wykresie kwartyle.
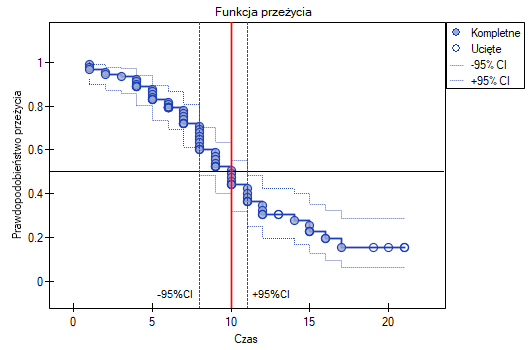
Przedział ufności dla mediany możemy zobrazować na wykresie wyrysowując linie pionowe w oparciu o przedział ufności wokół krzywej oraz linie na poziomie 0.5.
2014/08/24 23:44
· admin
statpqpl/survpl/wsteppl.txt · ostatnio zmienione: 2014/08/25 00:26 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

