Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat Knowledge Base » PQStat - Statistic » Survival analysis » Basics of survival analysis
Pasek boczny
en:statpqpl:survpl:wsteppl
Basics of survival analysis
Life tables
The window with settings for life tables is accessed via the menu Advanced statistics→Survival analysis→Life tables
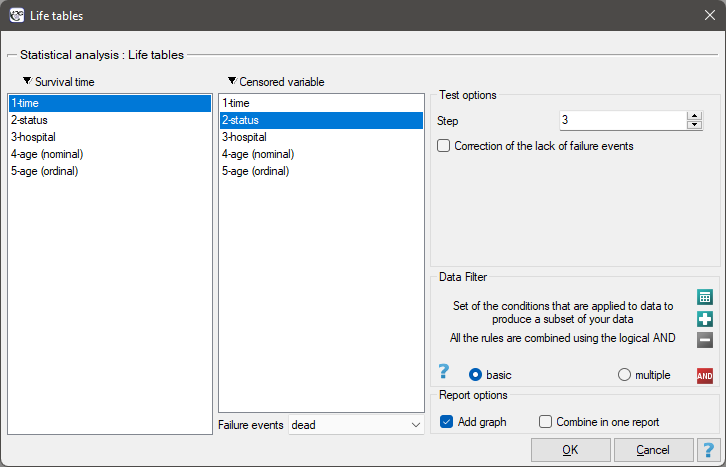
Life tables are created for time ranges with equal spans, provided by the researcher. The ranges can be defined by giving the step. For each range PQStat calculates:
- the number of entered cases – the number of people who survived until the time defined by the range;
- the number of censored cases – the number of people in a given range qualified as censored cases;
- the number of cases at risk – the number of people in a given range minus a half of the censored cases in the given range;
- the number of complete cases – the number of people who experienced the event (i.e. died) in a given range;
- proportions of complete cases – the proportion of the number of complete cases (deaths) in a given range to the number of the cases at risk in that range;
- proportions of the survival cases – calculated as 1 minus the proportion of complete cases in a given range;
- cumulative survival proportion (survival function) – the probability of surviving over a given period of time. Because to survive another period of time, one must have survived all the previous ones, the probability is calculated as the product of all the previous proportions of the survival cases.
 standard error of the survival function;
standard error of the survival function;
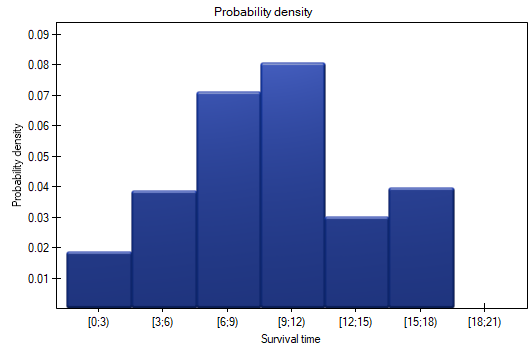
- probability density – the calculated probability of experiencing the event (death) in a given range, calculated in a period of time;
 standard error of the probability density;
standard error of the probability density;
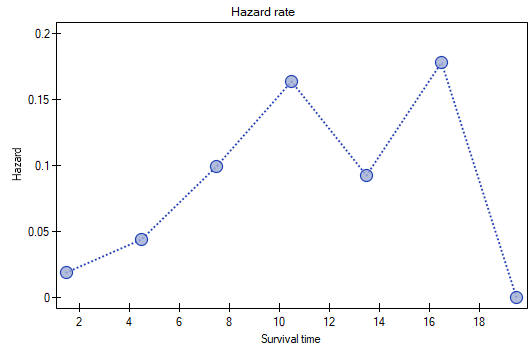
- hazard rate – probability (calculated per a unit of time) that a patient who has survived until the beginning of a given range will experience the event (die) in that range;
 standard error of the hazard rate
standard error of the hazard rate
Note
In the case of a lack of complete observations in any range of survival time range there is the possibility of using correction. The zero number of complete cases is then replaced with value 0.5.
Graphic interpretation
We can illustrate the information obtained thanks to the life tables with the use of several charts:
- a cumulative survival proportion graph,
- a probability density graph,
- a hazard rate graph.
Patients' survival rate after the transplantation of a liver was studied. 89 patients were observed over 21 years. The age of a patient at the time of the transplantation was in the range of 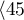 years
years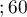 years
years . A fragment of the collected data is presented in the table below:
. A fragment of the collected data is presented in the table below:
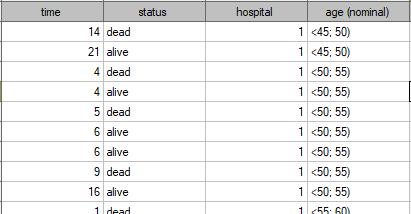
The complete data in the analysis are those as to which we have complete information about the length of life after the transplantation, i.e. described as „death” (it concerns 53 people which constitutes 59.55% of sample). The censored data are those about which we do not have that information because at the time when the study was finished the patients were alive (36 people, i.e. 40.45% of them). We build the life tables of those patients by creating time periods of 3 years:
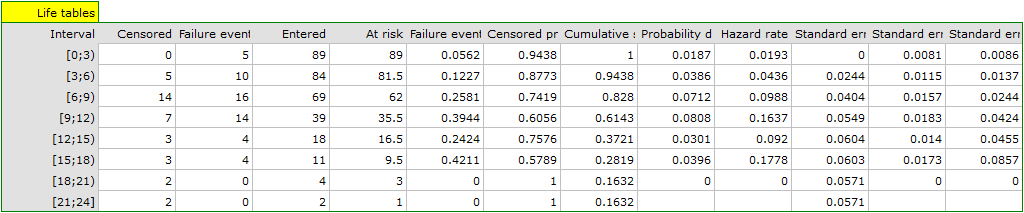
For each 3-year period of time we can interpret the results obtained in the table, for example, for people living for at least 9 years after the transplantation who are included in the range [9;12):
\item the number of people who survived 9 years after the transplantation is 39,
\item there are 7 people about whom we know they had lived at least 9-12 years at the moment the information about them was gathered but we do not know if they lived longer as they were left out of the study after that time,
\item the number of people at the risk of death in that age range is 36,
\item there are 14 people about whom we know they died 9 to 12 years after the transplantation,
\item 39.4% of the endangered patients died 9 to 12 years after the transplantation,
\item 60.6% of the endangered patients lived 9 to 12 years after the transplantation,
\item the percent of survivors 9 years after the transplantation is 61.4%  5%,
\item 0,08
5%,
\item 0,08  0.02 is the death probability for each year from the 9-12 range.
The results will be presented on a few graphs:
0.02 is the death probability for each year from the 9-12 range.
The results will be presented on a few graphs:
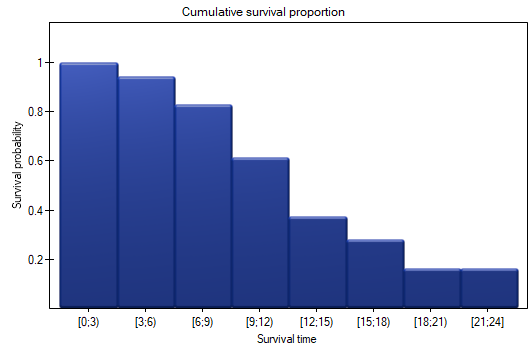
The probability of survival decreases with the time passed since the transplantation. We do not, however, observe a sudden plunge of the survival function, i.e. a period of time in which the probability of death would rise dramatically.
2022/02/09 12:56
Kaplan-Meier curves
Kaplan-Meier curves allow the evaluation of the survival time without the need to arbitrarily group the observations like in the case of life tables. The estimator was introduced by Kaplan and Meier (1958)\cite{kaplan}.
The window with settings for Kaplan-Meier curve is accessed via the menu Advanced statistics→Survival analysis→Kaplan-Meier Analysis
As with survival tables we calculate the survival function, i.e. the probability of survival until a certain time. The graph of the Kaplan-Meier survival function is created by a step function. Based on the standard error (Greenwood formula) and the logarithmic transformation (log-log), confidence intervals around this curve are constructed. The point of time at which the value of the function is 0.5 is the survival time median. The median indicates 50% risk of mortality, it means we can expect that half of the patients will die within a specific time. Both the median and other percentiles are determined as the shortest survival time for which the survival function is smaller or equal to a given percentile. For the median, a confidence interval is determined based on the test-based method by Brookmeyer and Crowley (1982)\cite{brookmeyer}. The survival time mean is determined as the field under the survival curve.
The data concerning the survival time are usually very heavily skewed so in the survival analysis the median is a better measure of the central tendency than the mean.
We present the survival time after a liver transplantation, with the use of the Kaplan-Meier curve
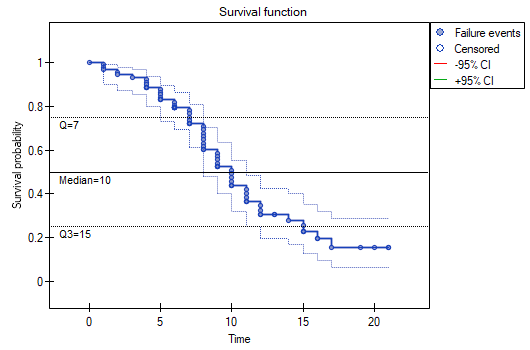

The survival function does not suddenly plunge right after the transplantation. Therefore, we conclude that the initial period after the transplantation does not carry a particular risk of death. The value of the median shows that within 10 years after the transplant, we expect that half of the patients will die. The value is marked on the graph by drawing a line in point 0.5 which signifies the median. In a similar manner we mark the quartiles in the graph.
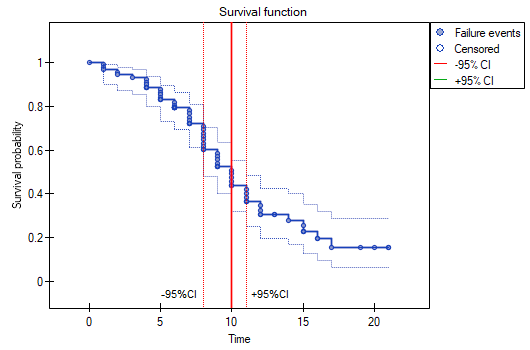
We can visualize the confidence interval for the median on a graph by drawing vertical lines based on the confidence interval around the curve and lines at the 0.5 level.
2022/02/09 12:56
en/statpqpl/survpl/wsteppl.txt · ostatnio zmienione: 2022/02/16 09:37 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

