Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:survpl:kmporpl:warstwpl
Krzywe przeżycia dla warstw
Często chcąc porównać czasy przeżycia dla dwóch lub więcej grup nie możemy zapomnieć o innych czynnikach, które mogą mieć wpływ na wynik tego porównania. Dostosowanie (korekcja) analizy o takie czynniki może być przydatna. Na przykład w badaniach domu opieki porównujących długość pobytu osób poniżej i powyżej 80 roku życia uzyskano istotną różnicę. Wiadomo jednak, że płeć ma silny związek z długością pobytu, a także wiekiem. Dlatego próbując ocenić wpływ wieku dobrym pomysłem byłaby stratyfikacja analizy ze względu na płeć.
Hipotezy dla różnic w krzywych przeżycia:
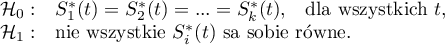
Hipotezy dla analizy trendu w krzywych przeżycia:
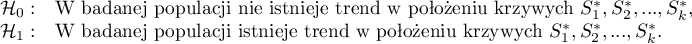
gdzie 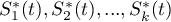 -to krzywe przeżycia po korekcji o zmienną wyznaczającą warstwy.
-to krzywe przeżycia po korekcji o zmienną wyznaczającą warstwy.
Obliczenia dla statystyk testowych bazują na formułach opisanych dla testów nie uwzględniających warstw z tą różnicą, że macierz U i V jest zastąpiona sumą macierzy 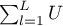 i
i 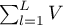 . Sumowanie następuje po warstwach utworzonych przez zmienną, względem której dostosowujemy (korygujemy) analizę (adjusted) l={1,2,…,L}
. Sumowanie następuje po warstwach utworzonych przez zmienną, względem której dostosowujemy (korygujemy) analizę (adjusted) l={1,2,…,L}
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Przykład c.d. (plik przeszczep.pqs)
Różnice dla dwóch krzywych przeżycia
Przeszczepy wątroby dokonywane były w dwóch różnych szpitalach. Sprawdzimy, czy długość życia pacjentów po przeszczepie zależały od szpitala, w którym dokonywano przeszczepu. Porównania krzywych przeżycia dla tych szpitali dokonamy w oparciu o wszystkie zaproponowane w programie testy służące temu porównaniu.
Hipotezy:
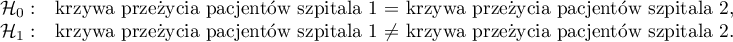

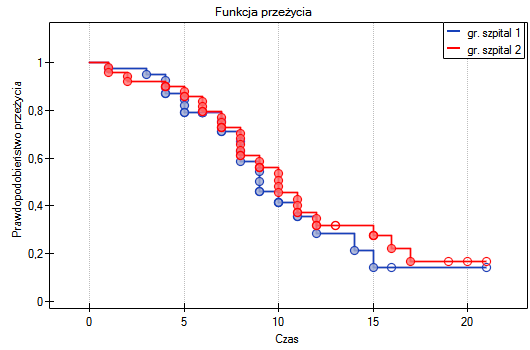
Na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
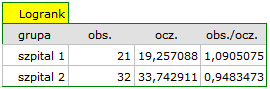
, w oparciu o uzyskaną wartość  =0.6004 dla testu log-rank (p=0.6959 dla Gehana i 0.6465 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę
=0.6004 dla testu log-rank (p=0.6959 dla Gehana i 0.6465 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę  . Długość życia wyliczona dla pacjentów obu tych szpitali jest podobna.
. Długość życia wyliczona dla pacjentów obu tych szpitali jest podobna.
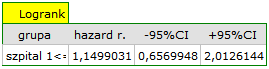
Do tego samego wniosku dojdziemy porównując ryzyko zgonu dla tych szpitali poprzez wyznaczenie ilorazu tego ryzyka. Uzyskana oszacowana wartość 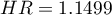 , a 95% przedział ufności dla tej wartości zawiera jedynkę:
, a 95% przedział ufności dla tej wartości zawiera jedynkę:  0.6570, 2.0126
0.6570, 2.0126 .
.
Różnice dla wielu krzywych przeżycia
Przeszczepy wątroby dokonywane były u ludzi w różnym wieku. Wyróżniono 3 grupy wiekowe: 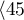 lat
lat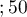 lat
lat ,
, 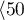 lat
lat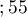 lat
lat ,
, 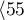 lat
lat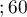 lat
lat . Sprawdzimy, czy długość życia pacjentów po przeszczepie zależy od ich wieku w chwili dokonania przeszczepu.
. Sprawdzimy, czy długość życia pacjentów po przeszczepie zależy od ich wieku w chwili dokonania przeszczepu.
Hipotezy:
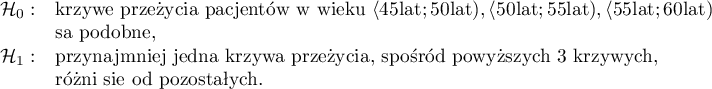
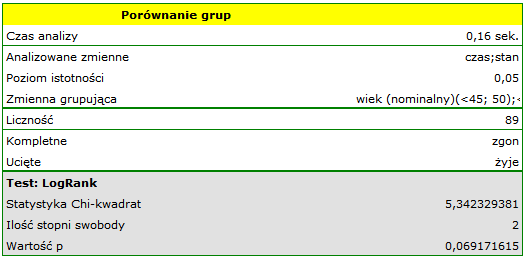
Na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
, w oparciu o uzyskaną wartość  =0.0692 w teście log-rank (p=0.09279 dla Gehana, p=0.0779 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę
=0.0692 w teście log-rank (p=0.09279 dla Gehana, p=0.0779 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę  . Długość życia wyliczona dla pacjentów należących do porównywanych trzech grup wiekowych jest podobna. Choć należy zauważyć że wartości p są dość bliskie standardowemu poziomowi istotności 0.05.
. Długość życia wyliczona dla pacjentów należących do porównywanych trzech grup wiekowych jest podobna. Choć należy zauważyć że wartości p są dość bliskie standardowemu poziomowi istotności 0.05.
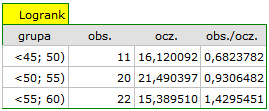
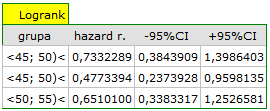
Przeglądając wartości hazardu (ilorazu wartości obserwowanych i oczekiwanych niepożądanych zdarzeń) zauważamy, że z każdą kategorią wiekową są one nieco wyższe  0.68, 0.93, 1.43
0.68, 0.93, 1.43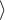 . Chociaż nie wykryto istotnych statystycznie różnic między nimi, to możliwe jest, że znaleziony zostanie trend wzrostu wartości hazardu (trend w położeniu krzywych przeżycia).
. Chociaż nie wykryto istotnych statystycznie różnic między nimi, to możliwe jest, że znaleziony zostanie trend wzrostu wartości hazardu (trend w położeniu krzywych przeżycia).
Trend dla kilku krzywych przeżycia
Jeśli do testu wprowadzimy informację dotyczącą uporządkowania porównywanych kategorii (wykorzystamy zmienną wiek, w której przedziały wiekowe ponumerujemy odpowiednio 1, 2 i 3), wówczas będziemy mogli sprawdzić, czy istnieje trend w porównywanych krzywych. Będziemy badać hipotezy:


Na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
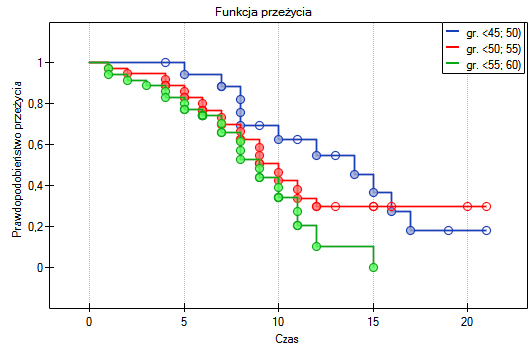
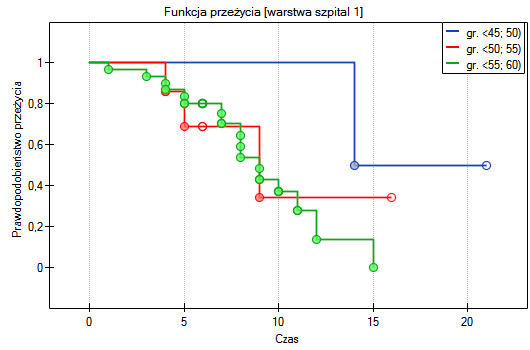
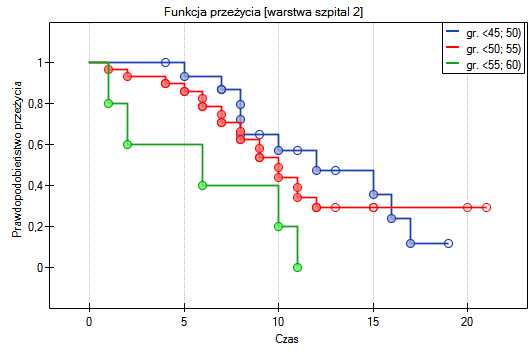
, w oparciu o uzyskaną wartość  =0.0237 w teście log-rank (p=0.0317 dla Gehana, p=0.0241 dla Tarona) wnioskujemy, że krzywe przeżycia ułożone są w pewnym trendzie. Najniżej na wykresie Kaplana-Meiera znajduje się krzywa dla osób w wieku
=0.0237 w teście log-rank (p=0.0317 dla Gehana, p=0.0241 dla Tarona) wnioskujemy, że krzywe przeżycia ułożone są w pewnym trendzie. Najniżej na wykresie Kaplana-Meiera znajduje się krzywa dla osób w wieku  55 lat; 60 lat). Nad nią jest krzywa dla pacjentów w wieku
55 lat; 60 lat). Nad nią jest krzywa dla pacjentów w wieku  50 lat; 55 lat). Najwyżej zaś krzywa dla pacjentów w wieku
50 lat; 55 lat). Najwyżej zaś krzywa dla pacjentów w wieku  45 lat; 50 lat). Zatem czym starszy pacjent w chwili przeszczepu, tym mniejsze prawdopodobieństwo przeżycia określonego odcinka czasu.
45 lat; 50 lat). Zatem czym starszy pacjent w chwili przeszczepu, tym mniejsze prawdopodobieństwo przeżycia określonego odcinka czasu.
Krzywe przeżycia dla warstw
Sprawdzimy teraz, czy obserwowany wcześniej trend jest niezależny od szpitala w którym dokonano przeszczepu. W tym celu jako zmienną warstwa wybierzemy szpital.
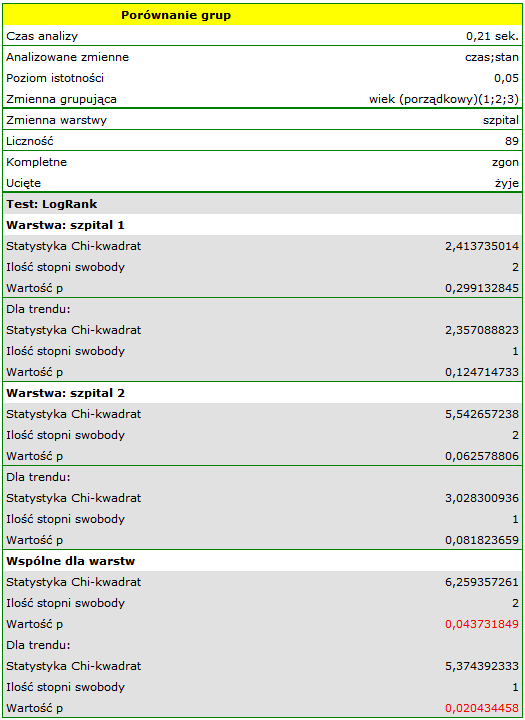
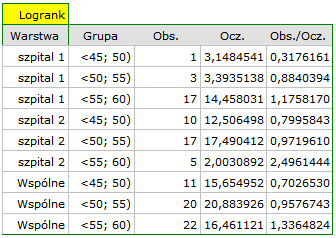
W raporcie najpierw przedstawiona jest analiza poszczególnych warstw, zarówno wyniki testów jak i wartości hazardu. W warstwie pierwszej trend wzrostu hazardu jest widoczny, choć nieistotny, trend o tym samym kierunku (wynik na pograniczu istotności statystycznej) obserwowany jest w warstwie drugiej. Kumulacja tych trendów we wspólnej analizie warstw pozwoliła uzyskać istotność trendu krzywych przeżycia. Zatem: czym starszy pacjent w chwili przeszczepu, tym mniejsze prawdopodobieństwo przeżycia określonego odcinka czasu niezależnie od szpitala dokonującego przeszczepu.
Analiza porównawcza krzywych przeżycia w korekcji o warstwy daje wynik istotny dla testu log-rank i Tarona a nieistotny dla Gehana, co może wskazywać na to, że pojawiające się różnice w krzywych nie są tak widoczne w początkowych okresach czasu przeżycia co w okresach późniejszych. Przyglądając się ilorazowi hazardu dla porównywanych parami krzywych
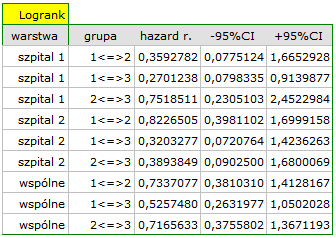
możemy zlokalizować istotne różnice. Najmniejszy iloraz hazardu mamy dla porównania krzywej dla najmłodszej grupy z krzywą dla grupy najstarszej 0.53, 95% przedział ufności dla tego ilorazu  0.26 ; 1.05
0.26 ; 1.05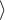 zawiera co prawda wartość 1, ale jest na pograniczu tej wartości, co może sugerować wystąpienie między odpowiadającymi im krzywymi istotnych różnic. By potwierdzić to przypuszczenie dociekliwy badacz, używając filtru danych w oknie analizy, może porównać krzywe parami.
zawiera co prawda wartość 1, ale jest na pograniczu tej wartości, co może sugerować wystąpienie między odpowiadającymi im krzywymi istotnych różnic. By potwierdzić to przypuszczenie dociekliwy badacz, używając filtru danych w oknie analizy, może porównać krzywe parami.

Należy jednak pamiętać by zastosować jedną z poprawek używanych przy wielokrotnych porównaniach i zmodyfikować poziom istotności. W tym przypadku dla poprawki Bonferroniego przy trzech porównaniach poziom istotności wyniesie 0.017. Dla uproszczenia rozważań posłużymy się tylko testem log-rank.
 45 lat; 50 lat) vs
45 lat; 50 lat) vs  50 lat; 55 lat)
50 lat; 55 lat)

 45 lat; 50 lat) vs
45 lat; 50 lat) vs  55 lat; 60 lat)
55 lat; 60 lat)

 50 lat; 55 lat) vs
50 lat; 55 lat) vs  55 lat; 60 lat)
55 lat; 60 lat)

Zgodnie z oczekiwaniem istotne statystycznie różnice dotyczą tylko krzywych przeżycia dla najmłodszej i najstarszej grupy wiekowej.
statpqpl/survpl/kmporpl/warstwpl.txt · ostatnio zmienione: 2019/04/03 22:02 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

