Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Analiza przeżycia » Porównywanie krzywych przeżycia
Pasek boczny
statpqpl:survpl:kmporpl
Spis treści
Porównywanie krzywych przeżycia
Funkcje przeżycia mogą być budowane oddzielnie dla różnych podgrup np. oddzielnie dla kobiet i mężczyzn, a następnie porównane między sobą. Takie porównanie może dotyczyć zarówno dwóch, jak i kilku krzywych.
Okno z ustawieniami opcji porównania krzywych przeżycia wywołujemy poprzez menu Statystyka→Analiza przeżycia→Porównanie grup
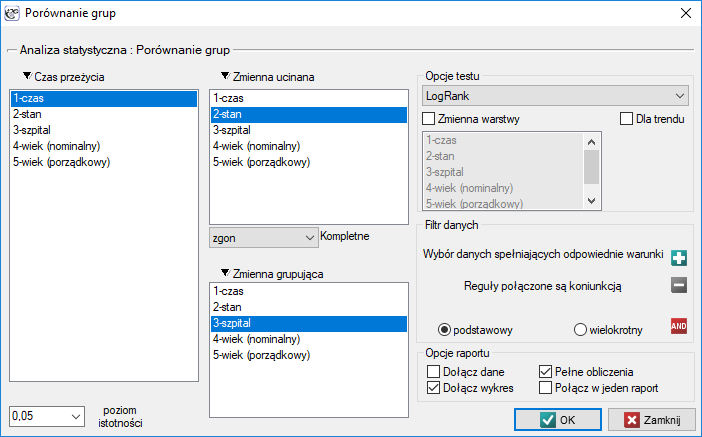
Porównania  krzywych przeżycia
krzywych przeżycia 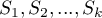 w poszczególnych punktach czasu przeżycia
w poszczególnych punktach czasu przeżycia  w programie możemy dokonać przy pomocy trzech testów:
w programie możemy dokonać przy pomocy trzech testów:
Testu log-rank najbardziej znanego i szeroko stosowanego, nawiązującego do procedury Mantela-Heanszela dla wielu tabel 2×2 (Mantel-Heanszel 19591), Mantel 19662), Cox 19723)),
Uogólnienia Gehana testu Wilcoxona wywodzącego się od testu Wilcoxona (Breslow 1970, Gehan 19654)5)),
Testu Taron-Ware wywodzącego się od testu Wilcoxona (Tarone i Ware 19776)).
Wszystkie trzy testy działają w oparciu o tę samą statystykę testową, inne są tylko wagi 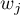 w poszczególnych punktach osi czasu, na których bazuje statystyka testowa.
w poszczególnych punktach osi czasu, na których bazuje statystyka testowa.
Test log-rank: 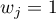 - wszystkie punkty osi czasu posiadają tę samą wagę, co daje większy wpływ na uzyskany wynik późniejszym wartościom osi czasu;
- wszystkie punkty osi czasu posiadają tę samą wagę, co daje większy wpływ na uzyskany wynik późniejszym wartościom osi czasu;
Uogólnienie Gehana testu Wilcoxona:  - momenty czasowe są ważone liczbą obserwacji w każdym z nich, a zatem przypisywane są większe wagi początkowym wartościom osi czasu;
- momenty czasowe są ważone liczbą obserwacji w każdym z nich, a zatem przypisywane są większe wagi początkowym wartościom osi czasu;
Test Taron-Ware: 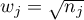 - momenty czasowe są ważone pierwiastkiem z liczby obserwacji w każdym z nich co powoduje, usytuowanie tego testu pomiędzy dwoma omówionymi wcześniej.
- momenty czasowe są ważone pierwiastkiem z liczby obserwacji w każdym z nich co powoduje, usytuowanie tego testu pomiędzy dwoma omówionymi wcześniej.
Ważnym warunkiem stosowania powyższych testów jest proporcjonalność hazardu. Hazard definiowany jako nachylenie krzywej przeżycia jest miarą tego, jak szybko następuje niepożądane zdarzenie. Złamanie założenia proporcjonalności hazardu choć nie dyskwalifikuje całkowicie powyższych testów, to niesie kilka niebezpieczeństw. Przede wszystkim położenie punktu przecięcia krzywych względem osi czasu ma decydujący wpływ na obniżenie mocy poszczególnych testów.
Przykład c.d. (plik przeszczep.pqs)
Różnice w krzywych przeżycia
Hipotezy:
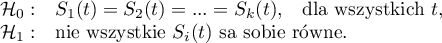
W obliczeniach wykorzystano statystykę chi-kwadrat postaci:
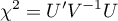 gdzie:
gdzie:
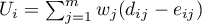
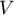 - macierz kowariancji o wymiarach
- macierz kowariancji o wymiarach 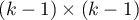
gdzie:
diagonala: 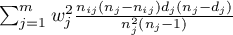 ,
,
poza diagonalą (off diagonal): 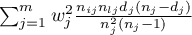
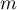 - liczba momentów czasowych, w których nastąpiło niepożądane zdarzenie (zgon),
- liczba momentów czasowych, w których nastąpiło niepożądane zdarzenie (zgon),
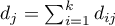 - obserwowana liczba niepożądanych zdarzeń (zgonów) w
- obserwowana liczba niepożądanych zdarzeń (zgonów) w  -tym momencie czasowym,
-tym momencie czasowym,
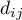 - obserwowana liczba niepożądanych zdarzeń (zgonów) w
- obserwowana liczba niepożądanych zdarzeń (zgonów) w  -tej grupie w
-tej grupie w  -tym momencie czasowym,
-tym momencie czasowym,
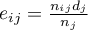 - oczekiwana liczba niepożądanych zdarzeń (zgonów) w
- oczekiwana liczba niepożądanych zdarzeń (zgonów) w  -tej grupie w
-tej grupie w  -tym momencie czasowym,
-tym momencie czasowym,
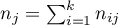 - liczba narażonych w
- liczba narażonych w  -tym momencie czasowym.
-tym momencie czasowym.
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z 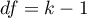 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Iloraz Hazardów
W teście Log-rank dla każdej grupy podawane są obserwowane wartości niepożądanych zdarzeń (zgonów) 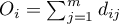 oraz odpowiednie wartości oczekiwane
oraz odpowiednie wartości oczekiwane 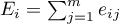 .
.
Miarą opisującą wielkość obserwowanej różnicy między parą krzywych przeżycia jest Iloraz Hazardów (ang. Hazard Ratio - 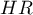 ).
).
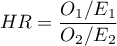
Jeśli Iloraz Hazardów jest większy niż 1 np. 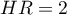 , to stopień narażenia na niepożądane zdarzenie w pierwszej grupie jest dwa razy większy niż w grupie drugiej. Odwrotna sytuacja jest gdy
, to stopień narażenia na niepożądane zdarzenie w pierwszej grupie jest dwa razy większy niż w grupie drugiej. Odwrotna sytuacja jest gdy 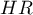 jest mniejsze niż jeden. Natomiast przy
jest mniejsze niż jeden. Natomiast przy 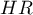 równym 1 obie grupy są narażone w tym samym stopniu.
równym 1 obie grupy są narażone w tym samym stopniu.
Uwaga!
Przedział ufności dla 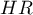 wyliczany jest w oparciu o błąd standardowy logarytmu
wyliczany jest w oparciu o błąd standardowy logarytmu 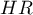 (Armitage i Berry 19947)).
(Armitage i Berry 19947)).
Przykład c.d. (plik przeszczep.pqs)
2014/08/22 20:00
Trend w krzywych przeżycia
Hipotezy:
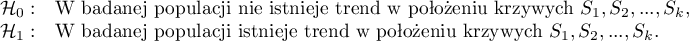
W obliczeniach wykorzystano statystykę chi-kwadrat postaci:
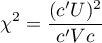
gdzie:
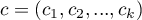
 wektor wag dla porównywanych grup informujący o ich naturalnym porządku (najczęściej kolejne liczby naturalne).
wektor wag dla porównywanych grup informujący o ich naturalnym porządku (najczęściej kolejne liczby naturalne).
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z jednym stopniem swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
By można było przeprowadzić analizę trendu w krzywych przeżycia, zmienna grupująca musi być zmienną liczbową, w której wartości liczb informują o naturalnym porządku grup. Liczby te w analizie traktowane są jako wagi 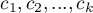 .
.
Przykład c.d. (plik przeszczep.pqs)
2014/08/22 20:00
Krzywe przeżycia dla warstw
Często chcąc porównać czasy przeżycia dla dwóch lub więcej grup nie możemy zapomnieć o innych czynnikach, które mogą mieć wpływ na wynik tego porównania. Dostosowanie (korekcja) analizy o takie czynniki może być przydatna. Na przykład w badaniach domu opieki porównujących długość pobytu osób poniżej i powyżej 80 roku życia uzyskano istotną różnicę. Wiadomo jednak, że płeć ma silny związek z długością pobytu, a także wiekiem. Dlatego próbując ocenić wpływ wieku dobrym pomysłem byłaby stratyfikacja analizy ze względu na płeć.
Hipotezy dla różnic w krzywych przeżycia:
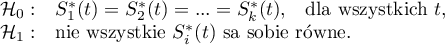
Hipotezy dla analizy trendu w krzywych przeżycia:
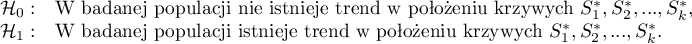
gdzie 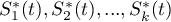 -to krzywe przeżycia po korekcji o zmienną wyznaczającą warstwy.
-to krzywe przeżycia po korekcji o zmienną wyznaczającą warstwy.
Obliczenia dla statystyk testowych bazują na formułach opisanych dla testów nie uwzględniających warstw z tą różnicą, że macierz U i V jest zastąpiona sumą macierzy 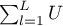 i
i 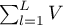 . Sumowanie następuje po warstwach utworzonych przez zmienną, względem której dostosowujemy (korygujemy) analizę (adjusted) l={1,2,…,L}
. Sumowanie następuje po warstwach utworzonych przez zmienną, względem której dostosowujemy (korygujemy) analizę (adjusted) l={1,2,…,L}
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Przykład c.d. (plik przeszczep.pqs)
Różnice dla dwóch krzywych przeżycia
Przeszczepy wątroby dokonywane były w dwóch różnych szpitalach. Sprawdzimy, czy długość życia pacjentów po przeszczepie zależały od szpitala, w którym dokonywano przeszczepu. Porównania krzywych przeżycia dla tych szpitali dokonamy w oparciu o wszystkie zaproponowane w programie testy służące temu porównaniu.
Hipotezy:
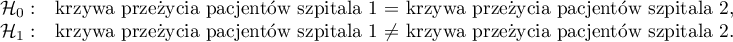

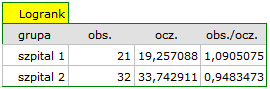
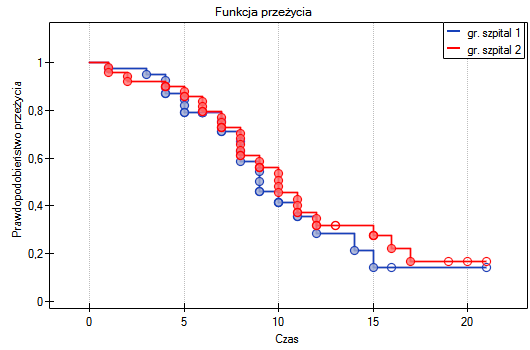
Na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
, w oparciu o uzyskaną wartość  =0.6004 dla testu log-rank (p=0.6959 dla Gehana i 0.6465 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę
=0.6004 dla testu log-rank (p=0.6959 dla Gehana i 0.6465 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę  . Długość życia wyliczona dla pacjentów obu tych szpitali jest podobna.
. Długość życia wyliczona dla pacjentów obu tych szpitali jest podobna.
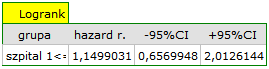
Do tego samego wniosku dojdziemy porównując ryzyko zgonu dla tych szpitali poprzez wyznaczenie ilorazu tego ryzyka. Uzyskana oszacowana wartość 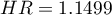 , a 95% przedział ufności dla tej wartości zawiera jedynkę:
, a 95% przedział ufności dla tej wartości zawiera jedynkę:  0.6570, 2.0126
0.6570, 2.0126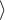 .
.
Różnice dla wielu krzywych przeżycia
Przeszczepy wątroby dokonywane były u ludzi w różnym wieku. Wyróżniono 3 grupy wiekowe: 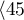 lat
lat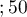 lat
lat ,
, 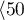 lat
lat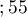 lat
lat ,
, 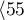 lat
lat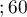 lat
lat . Sprawdzimy, czy długość życia pacjentów po przeszczepie zależy od ich wieku w chwili dokonania przeszczepu.
. Sprawdzimy, czy długość życia pacjentów po przeszczepie zależy od ich wieku w chwili dokonania przeszczepu.
Hipotezy:
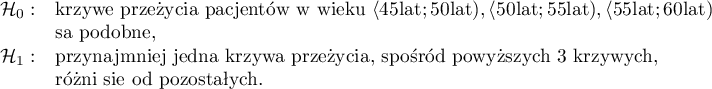
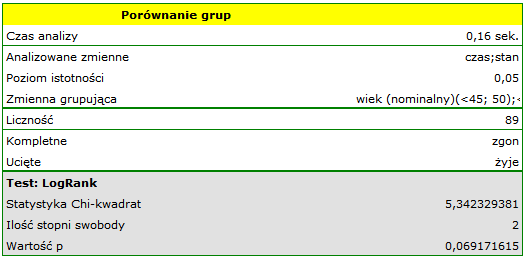
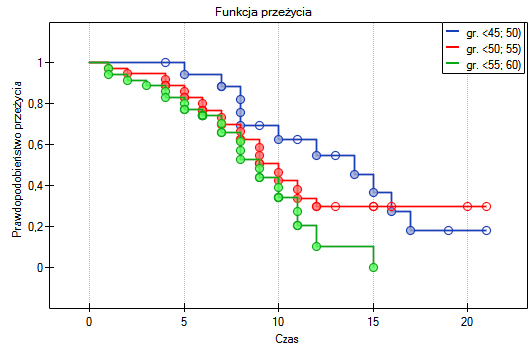
Na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
, w oparciu o uzyskaną wartość  =0.0692 w teście log-rank (p=0.09279 dla Gehana, p=0.0779 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę
=0.0692 w teście log-rank (p=0.09279 dla Gehana, p=0.0779 dla Tarona) wnioskujemy, że nie ma podstaw by odrzucić hipotezę  . Długość życia wyliczona dla pacjentów należących do porównywanych trzech grup wiekowych jest podobna. Choć należy zauważyć że wartości p są dość bliskie standardowemu poziomowi istotności 0.05.
. Długość życia wyliczona dla pacjentów należących do porównywanych trzech grup wiekowych jest podobna. Choć należy zauważyć że wartości p są dość bliskie standardowemu poziomowi istotności 0.05.
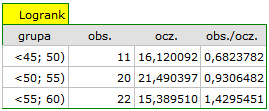
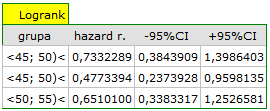
Przeglądając wartości hazardu (ilorazu wartości obserwowanych i oczekiwanych niepożądanych zdarzeń) zauważamy, że z każdą kategorią wiekową są one nieco wyższe  0.68, 0.93, 1.43
0.68, 0.93, 1.43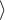 . Chociaż nie wykryto istotnych statystycznie różnic między nimi, to możliwe jest, że znaleziony zostanie trend wzrostu wartości hazardu (trend w położeniu krzywych przeżycia).
. Chociaż nie wykryto istotnych statystycznie różnic między nimi, to możliwe jest, że znaleziony zostanie trend wzrostu wartości hazardu (trend w położeniu krzywych przeżycia).
Trend dla kilku krzywych przeżycia
Jeśli do testu wprowadzimy informację dotyczącą uporządkowania porównywanych kategorii (wykorzystamy zmienną wiek, w której przedziały wiekowe ponumerujemy odpowiednio 1, 2 i 3), wówczas będziemy mogli sprawdzić, czy istnieje trend w porównywanych krzywych. Będziemy badać hipotezy:


Na podstawie przyjętego poziomu  , w oparciu o uzyskaną wartość
, w oparciu o uzyskaną wartość  =0.0237 w teście log-rank (p=0.0317 dla Gehana, p=0.0241 dla Tarona) wnioskujemy, że krzywe przeżycia ułożone są w pewnym trendzie. Najniżej na wykresie Kaplana-Meiera znajduje się krzywa dla osób w wieku
=0.0237 w teście log-rank (p=0.0317 dla Gehana, p=0.0241 dla Tarona) wnioskujemy, że krzywe przeżycia ułożone są w pewnym trendzie. Najniżej na wykresie Kaplana-Meiera znajduje się krzywa dla osób w wieku  55 lat; 60 lat). Nad nią jest krzywa dla pacjentów w wieku
55 lat; 60 lat). Nad nią jest krzywa dla pacjentów w wieku  50 lat; 55 lat). Najwyżej zaś krzywa dla pacjentów w wieku
50 lat; 55 lat). Najwyżej zaś krzywa dla pacjentów w wieku  45 lat; 50 lat). Zatem czym starszy pacjent w chwili przeszczepu, tym mniejsze prawdopodobieństwo przeżycia określonego odcinka czasu.
45 lat; 50 lat). Zatem czym starszy pacjent w chwili przeszczepu, tym mniejsze prawdopodobieństwo przeżycia określonego odcinka czasu.
Krzywe przeżycia dla warstw
Sprawdzimy teraz, czy obserwowany wcześniej trend jest niezależny od szpitala w którym dokonano przeszczepu. W tym celu jako zmienną warstwa wybierzemy szpital.
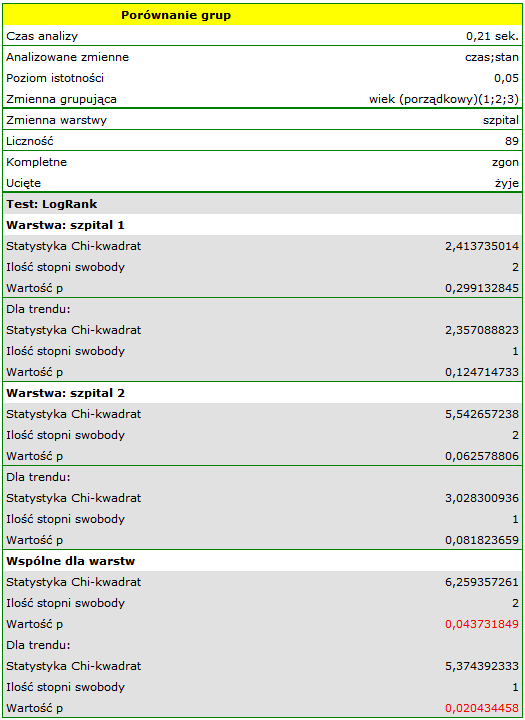
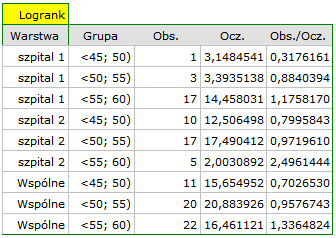
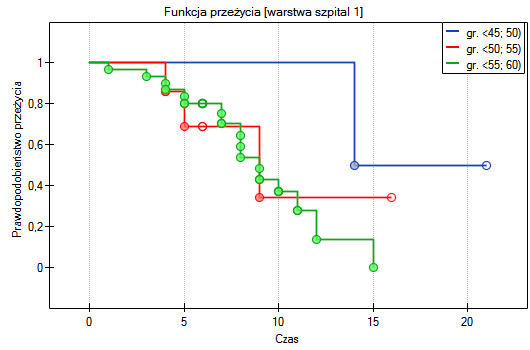
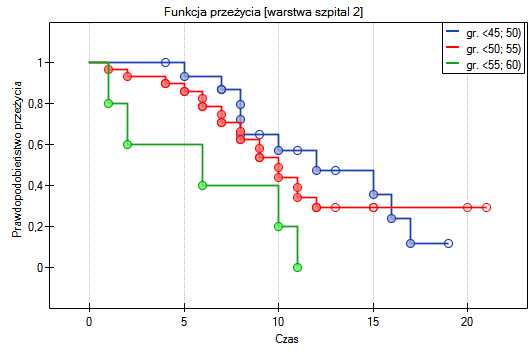
W raporcie najpierw przedstawiona jest analiza poszczególnych warstw, zarówno wyniki testów jak i wartości hazardu. W warstwie pierwszej trend wzrostu hazardu jest widoczny, choć nieistotny, trend o tym samym kierunku (wynik na pograniczu istotności statystycznej) obserwowany jest w warstwie drugiej. Kumulacja tych trendów we wspólnej analizie warstw pozwoliła uzyskać istotność trendu krzywych przeżycia. Zatem: czym starszy pacjent w chwili przeszczepu, tym mniejsze prawdopodobieństwo przeżycia określonego odcinka czasu niezależnie od szpitala dokonującego przeszczepu.
Analiza porównawcza krzywych przeżycia w korekcji o warstwy daje wynik istotny dla testu log-rank i Tarona a nieistotny dla Gehana, co może wskazywać na to, że pojawiające się różnice w krzywych nie są tak widoczne w początkowych okresach czasu przeżycia co w okresach późniejszych. Przyglądając się ilorazowi hazardu dla porównywanych parami krzywych
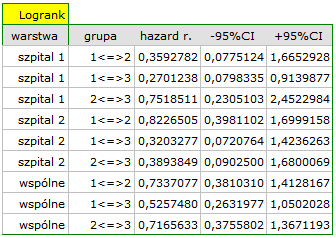
możemy zlokalizować istotne różnice. Najmniejszy iloraz hazardu mamy dla porównania krzywej dla najmłodszej grupy z krzywą dla grupy najstarszej 0.53, 95% przedział ufności dla tego ilorazu  0.26 ; 1.05
0.26 ; 1.05 zawiera co prawda wartość 1, ale jest na pograniczu tej wartości, co może sugerować wystąpienie między odpowiadającymi im krzywymi istotnych różnic. By potwierdzić to przypuszczenie dociekliwy badacz, używając filtru danych w oknie analizy, może porównać krzywe parami.
zawiera co prawda wartość 1, ale jest na pograniczu tej wartości, co może sugerować wystąpienie między odpowiadającymi im krzywymi istotnych różnic. By potwierdzić to przypuszczenie dociekliwy badacz, używając filtru danych w oknie analizy, może porównać krzywe parami.

Należy jednak pamiętać by zastosować jedną z poprawek używanych przy wielokrotnych porównaniach i zmodyfikować poziom istotności. W tym przypadku dla poprawki Bonferroniego przy trzech porównaniach poziom istotności wyniesie 0.017. Dla uproszczenia rozważań posłużymy się tylko testem log-rank.
 45 lat; 50 lat) vs
45 lat; 50 lat) vs  50 lat; 55 lat)
50 lat; 55 lat)

 45 lat; 50 lat) vs
45 lat; 50 lat) vs  55 lat; 60 lat)
55 lat; 60 lat)

 50 lat; 55 lat) vs
50 lat; 55 lat) vs  55 lat; 60 lat)
55 lat; 60 lat)

Zgodnie z oczekiwaniem istotne statystycznie różnice dotyczą tylko krzywych przeżycia dla najmłodszej i najstarszej grupy wiekowej.
2014/08/22 20:00
1)
Mantel N. and Haenszel W. (1959), Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute, 22,719-748
2)
Mantel N. (1966), Evaluation of Survival Data and Two New Rank Order Statistics Arising in Its Consideration. Cancer Chemotherapy Reports, 50:163—170
3)
Cox D.R. (1972), Regression models and life tables. Journal of the Royal Statistical Society, B34:187-220
4)
Gehan E. A. (1965a), A Generalized Wilcoxon Test for Comparing Arbitrarily Singly-Censored Samples. Biometrika, 52:203—223
5)
Gehan E. A. (1965b), A Generalized Two-Sample Wilcoxon Test for Doubly-Censored Data. Biometrika, 52:650—653
6)
Tarone R. E., Ware J. (1977), On distribution-free tests for equality of survival distributions. Biometrica, 64(1):156-160
7)
Armitage P., Berry G., (1994), Statistical Methods in Medical Research (3rd edition); Blackwell
statpqpl/survpl/kmporpl.txt · ostatnio zmienione: 2023/10/27 21:48 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


