PQStat - Baza Wiedzy

Metoda k-średnich

Metoda k-średnich (ang. k-means) wzoruje swoje działanie na algorytmie zaproponowanym początkowo przez Stuarta Lloyda i opublikowana w roku 1982 ¹⁾. W metodzie tej obiekty dzieli się na z góry założoną liczbę $k$ skupień. Początkowe skupienia poprawia się w toku wykonywania procedury aglomeracji, przenosząc pomiędzy nimi obiekty tak by zróżnicowanie obiektów wewnątrz skupienia było jak najmniejsze a odległości skupień jak największe. Algorytm działa w oparciu o macierz odległości euklidesowych pomiędzy obiektami, a parametrami niezbędnymi w procedurze aglomeracji metody k-średnich są: centra startowe i kryterium stopu. Centra startowe są to obiekty od których algorytm rozpocznie budowę skupień, a kryterium stopu to określenie sposobu zatrzymania algorytmu.

PROCEDURA AGLOMERACYJNA

Wybór centów startowych
Bazując na macierzy podobieństwa algorytm przypisuje każdy obiekt do najbliższego centrum
Dla uzyskanych skupień wyznacza się poprawione centra.
Kroki 2-3 są powtarzane aż do momentu spełnienia kryterium stopu.

Centra startowe

Wybór centrów startowych ma zasadniczy wpływ na zbieżność algorytmu k-średnich dla uzyskania odpowiednich skupień. Centra startowe mogą być wybrane na dwa sposoby:

k-means++ - to optymalny dobór punktów startowych poprzez wykorzystanie algorytmu k-means++ zaproponowanego w 2007 roku przez David Arthur and Sergei Vassilvitskii ²⁾. Gwarantuje on uzyskanie optymalnego rozwiązania algorytmu k-średnich przy możliwie niewielu iteracjach. Algorytm wykorzystuje w swoim działaniu element losowości, dlatego uzyskiwane wyniki mogą się nieco różnić przy kolejnych uruchomieniach analizy. Jeśli dane nie formułują się w naturalne klastery, lub jeśli nie można skutecznie podzielić danych na rozłączne skupiska, użycie k-means++ spowoduje uzyskanie zupełnie innych wyników w kolejnych uruchomieniach analizy k-średnich. Duża powtarzalność wyników świadczy natomiast o możliwości dokonania dobrego podziału na oddzielne skupienia.
n pierwszych - pozwala by użytkownik wskazał punkty będące centrami startowymi poprzez ustawienie tych obiektów na pierwszych miejscach w tabeli danych.

Kryterium stopu jest to moment, w którym nie zmienia się przynależność punktów do klas lub liczba powtórzeń kroku 2 i 3 algorytmu osiągnie zadaną przez użytkownika liczbę iteracji.

Ze względu na sposób działania algorytmu analizy skupień k-średnich, naturalną jej konsekwencją jest porównanie powstałych skupień przy pomocy jednoczynnikowej analizy wariancji (ANOVA) dla grup niezależnych.

Okno z ustawieniami opcji analizy skupień k-średnich wywołujemy poprzez menu Statystyki zaawansowane→Grupowanie i Redukcja→Analiza skupień k-średnich.

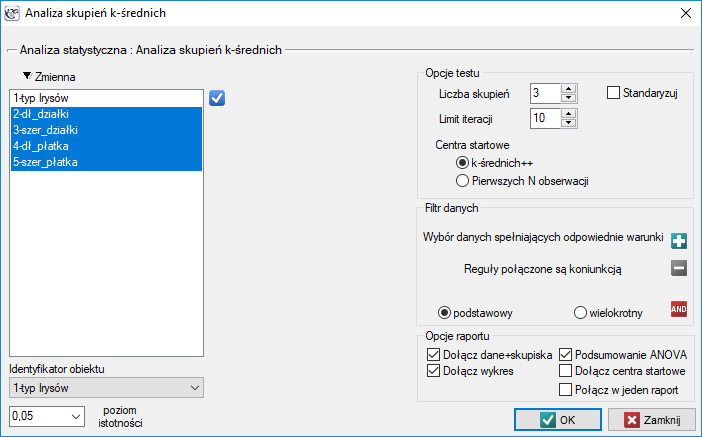
Przykład c.d. (plik iris.pqs)

Analiza przeprowadzona zostanie na klasycznym zestawie danych, dotyczącym podziału kwiatów irysa na 3 odmiany na podstawie szerokości oraz długości płatków i działek kielicha (R.A. Fishera 1936³⁾).

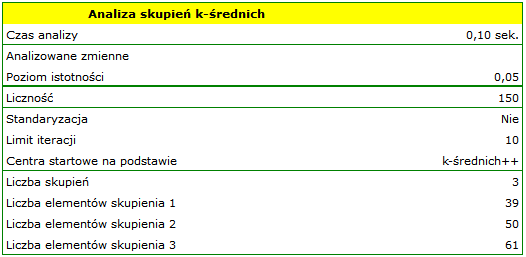
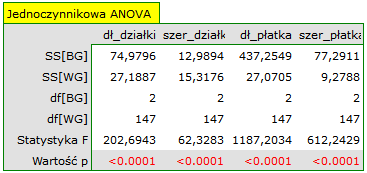
Przydziału kwiatów do poszczególnych grup dokonujemy na podstawie kolumn od 2 do 5. Wskazujemy również, że badane kwiaty chcemy podzielić na 3 grupy. W rezultacie przeprowadzonej analizy utworzono 3 skupienia, które różnią się istotnie statystycznie w każdym badanym wymiarze (wyniki ANOVA), czyli dla szerokości płatka, długości płatka, szerokości kielicha jaki i długości kielicha.

Różnicę można zaobserwować na wykresach, gdzie przedstawiamy w wybranych dwóch wymiarach przynależność poszczególnych punktów do skupień:

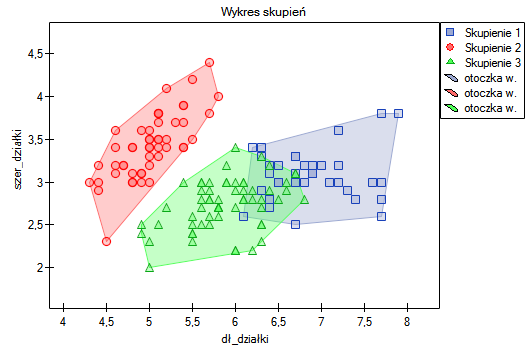
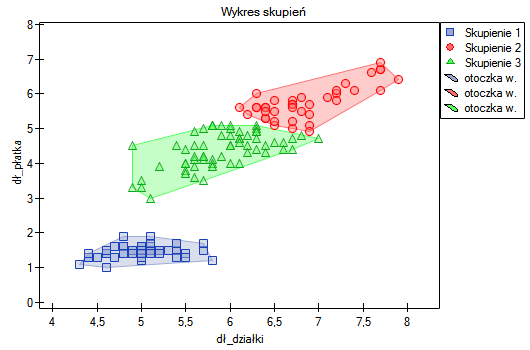
Powtarzając analizę możemy uzyskać nieco inne wyniki, ale uzyskana zmienność nie będzie duża. Świadczy to o tym, że dane poddane analizie formułują się w naturalne skupiska i przeprowadzanie analizy skupień jest w tym przypadku uzasadnione.

Uwaga 1! Po kilkukrotnym przeprowadzeniu analizy możemy wybrać najbardziej interesujący nas wynik, a następnie ustawić te dane, które stanowią centra startowe na początku arkusza - wówczas analiza przeprowadzona w oparciu o centra startowe wybierane jako N pierwszych obserwacji będzie dawała stale ten wybrany przez nas efekt.

Uwaga 2! By dowiedzieć się czy skupienia stanowią 3 rzeczywiste odmiany kwiatów irysa, możemy skopiować informację o przynależności do skupień z raportu i wkleić do arkusza danych. Zgodność naszych wyników z rzeczywistą przynależnością danego kwiatu do odpowiedniego gatunku możemy sprawdzić analogicznie jak dla hierarchicznej analizy skupień.

¹⁾

Lloyd S. P. (1982), Least squares quantization in PCM. IEEE Transactions on Information Theory 28 (2): 129–137

²⁾

Arthur D., Vassilvitskii S. (2007), k-means++: the advantages of careful seeding. Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics Philadelphia, PA, USA. 1027–1035

³⁾

Fisher R.A. (1936), The use of multiple measurements in taxonomic problems. Annals of Eugenics 7 (2): 179–188

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Metoda k-średnich

Narzędzia strony