Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:statpqpl:redpl:skupienpl:ksredpl
K-means method
K-means method is based on an algorithm initially proposed by Stuart Lloyd and published in 1982 1). In this method, objects are divided into a predetermined number of 
clusters. The initial clusters are adjusted during the agglomeration procedure by moving objects between them so that the variation of objects within the cluster is as small as possible and the cluster distances are as large as possible. The algorithm works on the basis of the matrix of Euclidean distances between objects, and the parameters necessary in the procedure of agglomeration of the k-means method are: starting centers and stopping criterion. The starting centers are the objects from which the algorithm will start building clusters, and the stopping criterion is the definition of how to stop the algorithm.
AGGLOMERATION PROCEDURE
- Selection of starting centers
- Based on the similarity matrix, the algorithm assigns each object to the nearest center
- For the clusters obtained, the adjusted centers are determined.
- Steps 2-3 are repeated until the stop criterion is met.
Starting centers
The choice of starting centers has a major impact on the convergence of the k-means algorithm for obtaining appropriate clusters. The starting centers can be selected in two ways:
- k-means++ - is the optimal selection of starting points by using the k-means++ algorithm proposed in 2007 by David Arthur and Sergei Vassilvitskii 2). It ensures that the optimal solution of the k-means algorithm is obtained with as few iterations as possible. The algorithm uses an element of randomness in its operation, so the results obtained may vary slightly with successive runs of the analysis. If the data do not form into natural clusters, or if the data cannot be effectively divided into disconnected clusters, using k-means++ will result in completely different results in subsequent runs of the k-means analysis. High reproducibility of the results, on the other hand, demonstrates the possibility of good division into separable clusters.
- n firsts - allows the user to indicate points that are start centers by placing these objects in the first positions in the data table.
Stop criterion is the moment when the belonging of the points to the classes does not change or the number of iterations of steps 2 and 3 of the algorithm reaches a user-specified number of iterations.
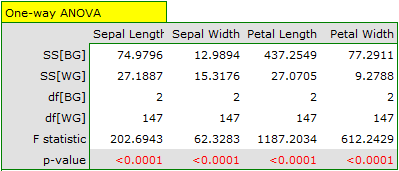
Because of the way the k-means cluster analysis algorithm works, a natural consequence of it is to compare the resulting clusters using a one-way analysis of variance (**ANOVA**) for independent groups.
Settings window of the k-means cluster analysis is opened via menu Advanced Statistics→Reduction and grouping→K-means cluster analysis.
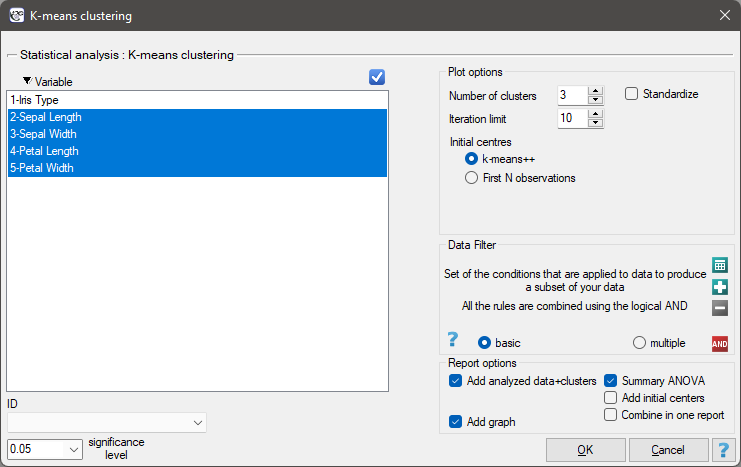
EXAMPLE cont. (iris.pqs file)
The analysis will be performed on the classic data set of dividing iris flowers into 3 varieties based on the width and length of the petals and sepal sepals (R.A. Fisher 19363)).
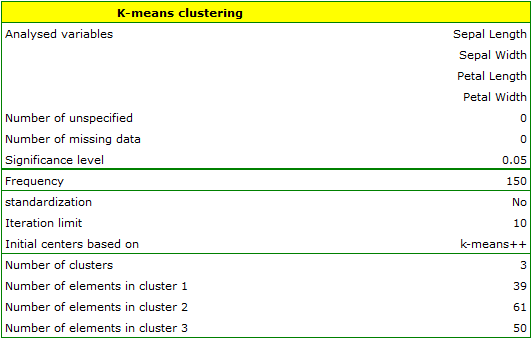
We assign flowers to particular groups on the basis of columns from 2 to 5. We also indicate that we want to divide the flowers into 3 groups. As a result of the analysis, 3 clusters were formed, which differed statistically significantly in each of the examined dimensions (ANOVA results), i.e. petal width, petal length, sepal width as well as sepal length.
The difference can be observed in the graphs where we show the belonging of each point to a cluster in the two dimensions selected:
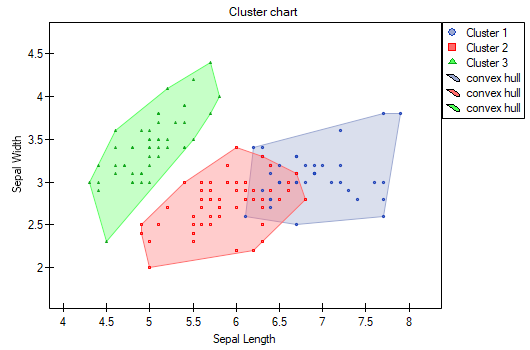
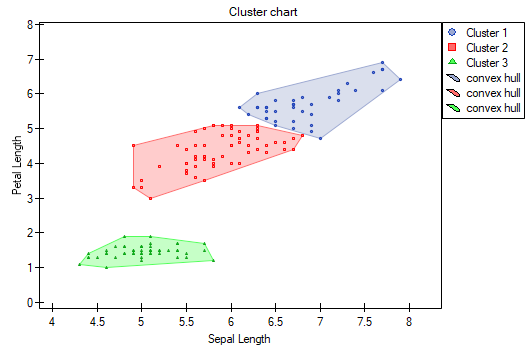
By repeating the analysis we may get slightly different results, but the variation obtained will not be large. It proves that data subjected to analysis form natural clusters and conducting a cluster analysis is justified in this case.
Note no.1!
After running the analysis a few times, we can select the result we are most interested in, and then set those data that are the starting centers at the beginning of the worksheet - then the analysis performed based on the starting centers selected as N first observations will consistently produce that result we selected.
Note no.2!
To find out if the clusters represent the 3 actual varieties of iris flowers, we can copy the information about belonging to a cluster from the report and paste it into the datasheet. We can check the consistency of our results with the actual affiliation of a given flower to the corresponding variety in the same way as for the hierarchical cluster analysis.
1)
Lloyd S. P. (1982), Least squares quantization in PCM. IEEE Transactions on Information Theory 28 (2): 129–137
2)
Arthur D., Vassilvitskii S. (2007), k-means++: the advantages of careful seeding. Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics Philadelphia, PA, USA. 1027–1035
3)
Fisher R.A. (1936), The use of multiple measurements in taxonomic problems. Annals of Eugenics 7 (2): 179–188
en/statpqpl/redpl/skupienpl/ksredpl.txt · ostatnio zmienione: 2022/03/15 21:03 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International
