Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown3grpl:nparpl:j_terpstrpl
Test Jonckheere-Terpstra dla trendu
Test Jonckheere-Terpstra dla trendu (ang. the Jonckheere-Terpstra test for ordered alternatives) opisany niezależnie przez Jonckheere (1954) 1) i Terpstra (1952)2) może być wyliczany w takiej samej sytuacji jak ANOVA Kruskala-Wallisa, gdyż bazuje na tych samych założeniach. Test Jonckheere-Terpstra inaczej jednak ujmuje hipotezę alternatywną - wskazując w niej na istnienie trendu dla kolejnych populacji.
Hipotezy są upraszczane do median:
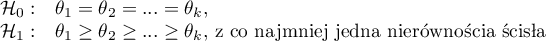
Uwaga!
Określenie: „z co najmniej jedną nierównością ścisłą” zapisane w hipotezie alternatywnej tego testu oznacza, że co najmniej mediana jednej populacji powinna być większa niż mediana innej populacji w kolejności określonej.
Statystyka testowa ma postać:
![LaTeX \begin{displaymath}
Z=\frac{L-\left[\frac{N^2-\sum_{j=1}^kn_j^2}{4}\right]}{SE}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img90c514ede7a37557872f285e3a796486.png)
gdzie:
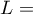 - suma wartości
- suma wartości 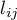 uzyskanych dla każdej pary porównywanych populacji,
uzyskanych dla każdej pary porównywanych populacji,
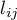 - liczba wyników wyższych niż zadana wartość w grupie występującej w następnej kolejności,
- liczba wyników wyższych niż zadana wartość w grupie występującej w następnej kolejności,
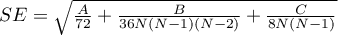 ,
,
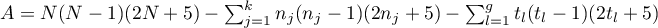 ,
,
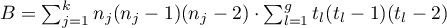 ,
,
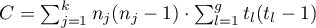 ,
,
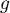 - liczba grup różnych rang wiązanych,
- liczba grup różnych rang wiązanych,
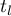 -liczba przypadków wchodzących w skład rangi wiązanej,
-liczba przypadków wchodzących w skład rangi wiązanej,
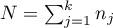 ,
,
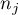 - liczności prób dla
- liczności prób dla  .
.
Uwaga!
By można było przeprowadzić analizę trendu, należy wskazać oczekiwaną kolejność populacji przypisując im kolejne liczby naturalne.
Wzór na statystykę testową  zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych wzór na statystykę testową sprowadza się do oryginalnej formuły Jonckheere-Terpstra nie zawierającej tej poprawki).
zawiera poprawkę na rangi wiązane. Poprawka ta jest stosowana, gdy rangi wiązane występują (gdy nie ma rang wiązanych wzór na statystykę testową sprowadza się do oryginalnej formuły Jonckheere-Terpstra nie zawierającej tej poprawki).
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Przy znanym oczekiwanym kierunku trendu, hipoteza alternatywna jest jednostronna i interpretacji podlega jednostronna wartość  . Interpretacja dwustronnej wartości
. Interpretacja dwustronnej wartości  oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość
oznacza, że badacz nie zna (nie zakłada) kierunku ewentualnego trendu. Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

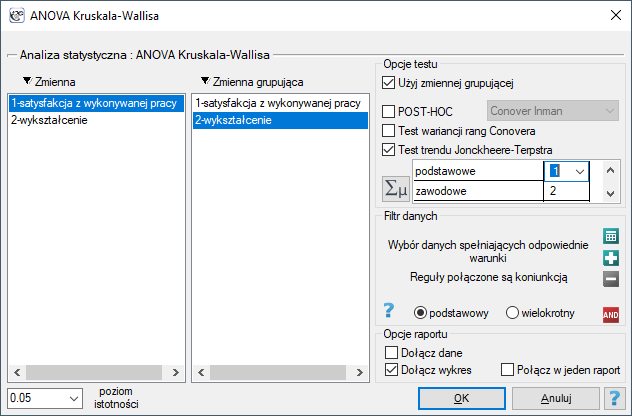
Okno z ustawieniami opcji testu Jonckheere-Terpstra wywołujemy poprzez menu Statystyka→Testy nieparametryczne→ANOVA Kruskala-Wallisa lub poprzez Kreator.
Pprzykład c.d. (plik satysfakcjaZpracy.pqs)
Podejrzewa się, że osoby lepiej wykształcone mają wysokie wymagania zawodowe, co może zmniejszać poziom satysfakcji z pierwszej pracy, która często takich wymagań nie spełnia. Dlatego też warto przeprowadzić analizę trendu.
Hipotezy:
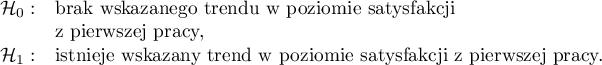
W tym celu wznawiamy analizę przyciskiem  , zaznaczamy opcję
, zaznaczamy opcję Test trendu Jonckheere-Terpstra i kolejnym kategoriom wykształcenia przypisujemy kolejne liczby naturalne.
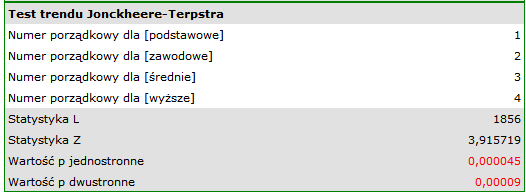
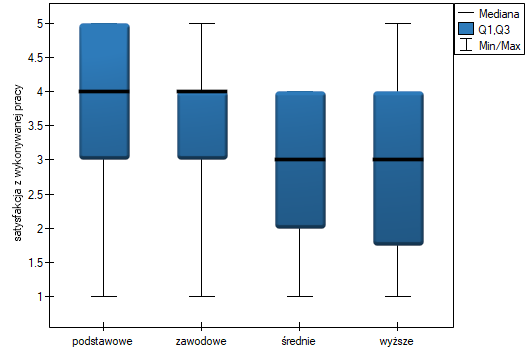
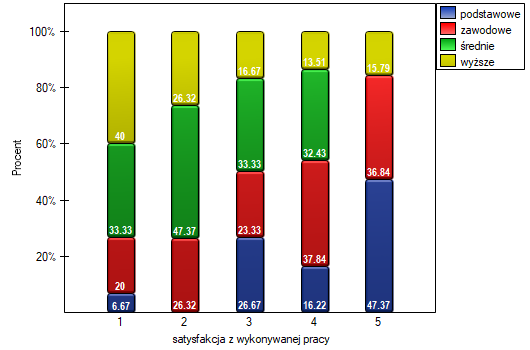
Uzyskana jednostronna wartość 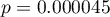 i jest mniejsza niż zadany poziom istotności
i jest mniejsza niż zadany poziom istotności  , co przemawia na rzecz rzeczywiście występującego trendu zgodnego z oczekiwaniami badacza.
, co przemawia na rzecz rzeczywiście występującego trendu zgodnego z oczekiwaniami badacza.
Istnienie tego trendu możemy również potwierdzić przedstawiając procentowy rozkład uzyskanych odpowiedzi.
statpqpl/porown3grpl/nparpl/j_terpstrpl.txt · ostatnio zmienione: 2022/07/14 11:58 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


