Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:statpqpl:porown3grpl:nparpl:j_terpstrpl
The Jonckheere-Terpstra test for trend
The Jonckheere-Terpstra test for ordered alternatives described independently by Jonckheere (1954) 1) an be calculated in the same situation as the Kruskal-Wallis ANOVA , as it is based on the same assumptions. The Jonckheere-Terpstra test, however, captures the alternative hypothesis differently - indicating in it the existence of a trend for successive populations.
Hypotheses are simplified to medians:
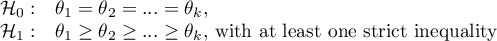
Note
The term: „with at least one strict inequality” written in the alternative hypothesis of this test means that at least the median of one population should be greater than the median of another population in the order specified.
The test statistic has the form:
![LaTeX \begin{displaymath}
Z=\frac{L-\left[\frac{N^2-\sum_{j=1}^kn_j^2}{4}\right]}{SE}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img90c514ede7a37557872f285e3a796486.png)
where:
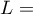 – sum of
– sum of 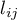 values obtained for each pair of compared populations,
values obtained for each pair of compared populations,
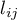 – number of results higher than a preset value in the next occurring group,
– number of results higher than a preset value in the next occurring group,
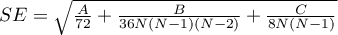 ,
,
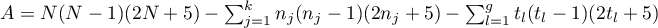 ,
,
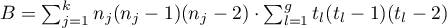 ,
,
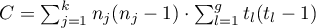 ,
,
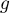 – number of groups of different tied ranks,
– number of groups of different tied ranks,
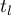 – umber of cases included in the tied rank,
– umber of cases included in the tied rank,
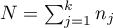 ,
,
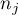 – sample sizes for
– sample sizes for  .
.
Note
To be able to perform a trend analysis, the expected order of the populations must be indicated by assigning consecutive natural numbers.
The formula for the test statistic  includes the correction for ties. This correction is applied when tied ranks are present (when there are no tied ranks the test statistic formula reduces to the original Jonckheere-Terpstra formula without this correction).
includes the correction for ties. This correction is applied when tied ranks are present (when there are no tied ranks the test statistic formula reduces to the original Jonckheere-Terpstra formula without this correction).
The statistic  has asymptotically (for large samples) normal distribution.
has asymptotically (for large samples) normal distribution.
With the expected direction of the trend known, the alternative hypothesis is one-sided and the one-sided p-value is interpreted. The interpretation of the two-sided p-value means that the researcher does not know (does not assume) the direction of the possible trend.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

The settings window with the Jonckheere-Terpstra test for trend can be opened in Statistics menu→NonParametric tests→Kruskal-Wallis ANOVA or in ''Wizard''.
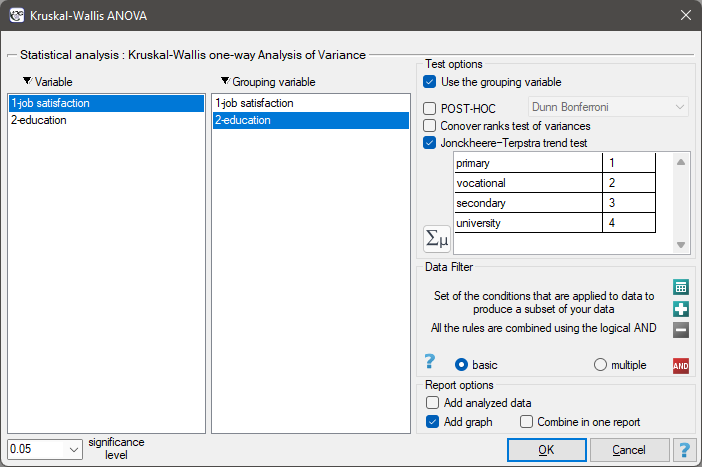
EXAMPLE cont. (jobSatisfaction.pqs file)
It is suspected that better educated people have high job demands, which may reduce the satisfaction level of the first job, which often does not meet such demands. Therefore, it is worthwhile to conduct a trend analysis.
Hypotheses:
To do this, we resume the analysis with the  button, select the
button, select the Jonckheere-Terpstra trend test option, and assign successive natural numbers to the education categories.
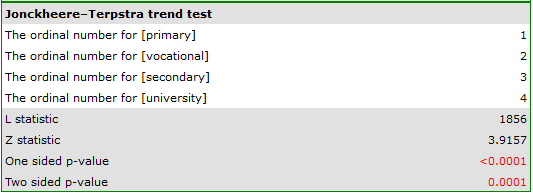
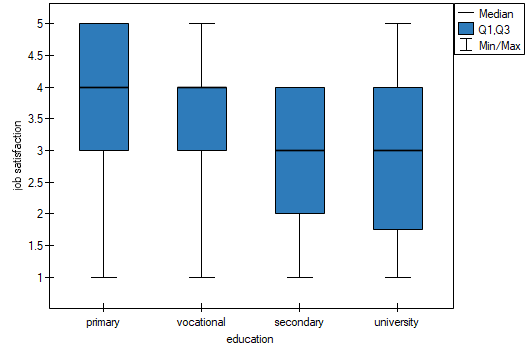
The obtained one-sided value p<0.0001 and is less than the set significance level  , which speaks in favor of a trend actually occurring consistent with the researcher's expectations.
, which speaks in favor of a trend actually occurring consistent with the researcher's expectations.
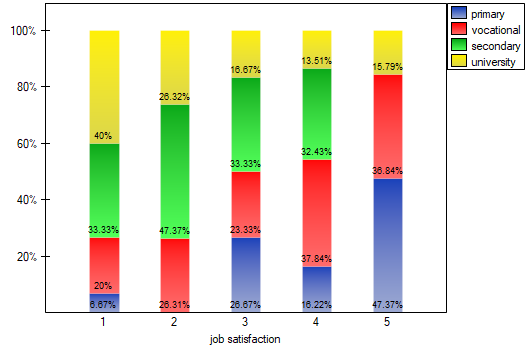
We can also confirm the existence of this trend by showing the percentage distribution of responses obtained.
1)
Jonckheere A. R. (1954), A distribution-free k-sample test against ordered alternatives. Biometrika, 41: 133–145) and Terpstra (1952)((Terpstra T. J. (1952), The asymptotic normality and consistency of Kendall's test against trend, when ties are present in one ranking. Indagationes Mathematicae, 14: 327–333
en/statpqpl/porown3grpl/nparpl/j_terpstrpl.txt · ostatnio zmienione: 2022/07/14 12:05 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

