PQStat - Baza Wiedzy

Test chi-kwadrat dla wielowymiarowych tabel kontyngencji

Test $\chi^2$ dla wielowymiarowych tabel kontyngencji (ang. Chi-square test for multidimensional contingency tables) jest rozszerzeniem testu chi-kwadrat dla tabel (RxC) na więcej niż dwie cechy.

Podstawowe warunki stosowania:

pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę,
model niezależny,
duże liczności oczekiwane według interpretacji Cochrana (1952)¹⁾.

Hipotezy:

$\begin{array}{cl} \mathcal{H}_0: & O_{ij...}=E_{ij...} $ dla wszystkich kategorii,$\\ \mathcal{H}_1: & O_{ij...} \neq E_{ij...} $ dla przynajmniej jednej kategorii,$ \end{array}$

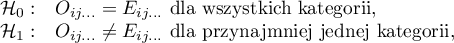
gdzie:

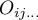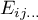$O_{ij...}$ i $E_{ij...}$ to liczności obserwowane w tabeli kontyngencji i odpowiadające im liczności oczekiwane.

Statystyka testowa ma postać:

$\begin{displaymath} \chi^2=\sum_{i=1}^r\sum_{j=1}^c\sum...\sum\frac{(O_{ij...}-E_{ij...})^2}{E_{ij...}}. \end{displaymath}$

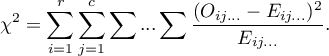
Statystyka ta ma asymptotycznie (dla dużych liczności oczekiwanych) rozkład chi-kwadrat z liczbą stopni swobody wyznaczaną według wzoru: 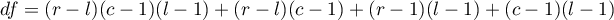$df = (r - l)(c - 1)(l - 1) + (r- l)(c- 1) + (r- 1)(l- 1) + (c- 1)(l- 1)$ - dla tabeli o 3 wymiarach.

Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

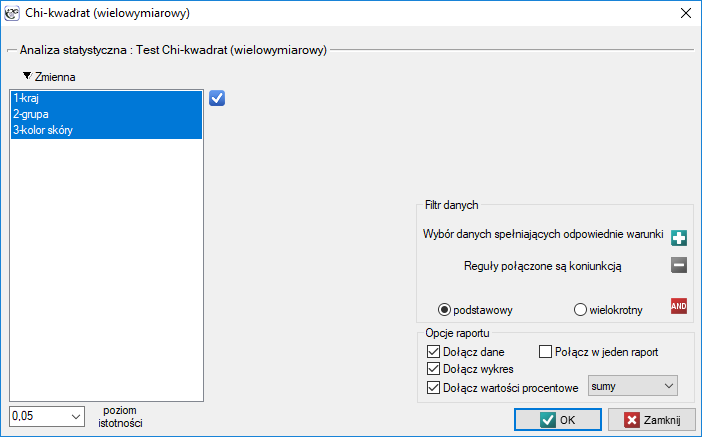
Okno z ustawieniami opcji wielowymiarowego testu chi-kwadrat wywołujemy poprzez menu Statystyka→Testy nieparametryczne→chi-kwadrat (wielowymiarowy) lub poprzez ''Kreator''.

Uwaga!

Test ten jest możliwy do wyliczenia tylko na podstawie danych surowych.

¹⁾

Cochran W.G. (1952), The chi-square goodness-of-fit test. Annals of Mathematical Statistics, 23, 315-345

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Test chi-kwadrat dla wielowymiarowych tabel kontyngencji

Narzędzia strony