Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
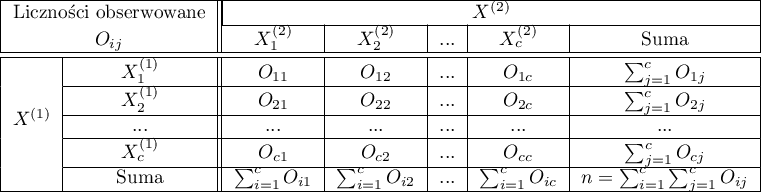
statpqpl:porown2grpl:nparpl:mcnemarrpl
Test McNemara, test wewnętrznej symetrii Bowkera
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę,
Test McNemara (ang. McNemar test), NcNemar (1947)1). Test ten służy do weryfikacji hipotezy o zgodności pomiędzy wynikami dwukrotnych pomiarów 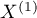 i
i 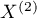 cechy
cechy  (pomiędzy dwiema zmiennymi zależnymi
(pomiędzy dwiema zmiennymi zależnymi 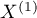 i
i 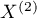 ). Badana cecha może mieć tylko 2 kategorie (oznaczone przez nas
). Badana cecha może mieć tylko 2 kategorie (oznaczone przez nas 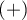 i
i 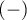 ). Test McNemara można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach
). Test McNemara można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach 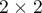 .
.

Hipotezy:
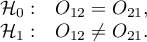
Statystyka testowa ma postać:
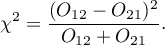
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z jednym stopniem swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Poprawka na ciągłość testu McNemara
Poprawka ta jest testem bardziej konserwatywny od testu McNemara (trudniej niż test McNemara odrzuca hipotezę zerową). Ma ona zapewnić możliwość przyjmowania przez statystykę testową wszystkich wartości liczb rzeczywistych zgodnie z założeniem rozkładu  . Część źródeł podaje, że poprawkę na ciągłość powinno się wykonywać zawsze, natomiast część uznaje, że tylko wtedy, gdy liczności w tabeli są małe.
. Część źródeł podaje, że poprawkę na ciągłość powinno się wykonywać zawsze, natomiast część uznaje, że tylko wtedy, gdy liczności w tabeli są małe.
Statystyka testowa testu McNemara z poprawką na ciągłość ma postać:
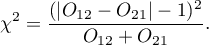
Dokładny test McNemara
Powszechną, ogólną zasadą ważności asymptotycznego testu McNemara chi-kwadrat jest warunek Rufibach, czyli to, że liczba niezgodnych par jest większa niż 10: 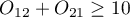 2), gdy warunek ten nie jest spełniony, wówczas powinniśmy bazować na dokładnych wartościach prawdopodobieństwa tego testu 3). Dokładna wartość prawdopodobieństwa testu oparta jest o rozkład dwumianowy i jest testem konserwatywnym, dlatego obok dokładnej wartości testu MnNemara podano również polecaną wartość dokładną mid-p testu McNemara.
2), gdy warunek ten nie jest spełniony, wówczas powinniśmy bazować na dokładnych wartościach prawdopodobieństwa tego testu 3). Dokładna wartość prawdopodobieństwa testu oparta jest o rozkład dwumianowy i jest testem konserwatywnym, dlatego obok dokładnej wartości testu MnNemara podano również polecaną wartość dokładną mid-p testu McNemara.
Jeśli przeprowadzone zostało 2 krotnie badanie tej samej cechy na tych samych obiektach - wówczas dla takiej tabeli wylicza się iloraz szans na zmianę wyniku (z 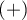 na
na 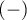 i odwrotnie).
i odwrotnie).
Szansa zmiany wyniku z 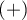 na
na 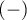 wynosi
wynosi 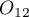 , a szansa zmiany wyniku z
, a szansa zmiany wyniku z 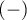 na
na 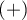 wynosi
wynosi 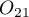 .
.
Iloraz szans (ang. odds ratio - OR) to:
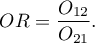
Przedział ufności dla ilorazu szans buduje się w oparciu o błąd standardowy:
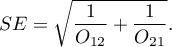
Uwaga!
Dodatkowo, dla prób o niewielkich licznościach, można wyznaczyć dokładny zakres przedziału ufności dla Ilorazu Szans 4).
Okno z ustawieniami opcji testu Bowkera-McNemara wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Bowker-McNemar lub poprzez ''Kreator''.
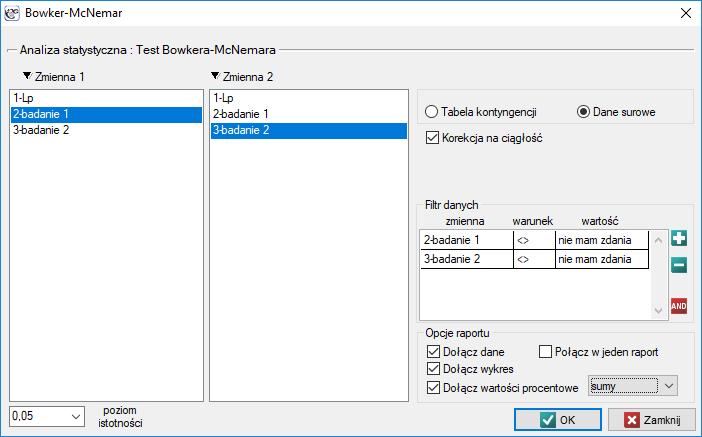
Test wewnętrznej symetrii Bowkera
Test wewnętrznej symetrii Bowkera (ang. Bowker test of internal symmetry), Bowker (1948)5). Test ten jest rozszerzeniem testu McNemara na 2 zmienne o więcej niż dwóch kategoriach (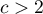 ). Służy do weryfikacji hipotezy o symetryczności wyników dwukrotnych pomiarów
). Służy do weryfikacji hipotezy o symetryczności wyników dwukrotnych pomiarów 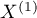 i
i 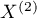 cechy
cechy  (symetryczności 2 zmiennych zależnych
(symetryczności 2 zmiennych zależnych 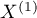 i
i 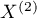 ). Badana cecha może mieć więcej niż 2 kategorie. Test wewnętrznej symetrii Bowker można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach
). Badana cecha może mieć więcej niż 2 kategorie. Test wewnętrznej symetrii Bowker można wyliczać na podstawie danych surowych albo z wykonanej na podstawie danych surowych tabeli kontyngencji o wymiarach 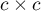 .
.
Hipotezy:
gdzie  ,
,  ,
, 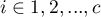 , zatem
, zatem 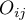 i
i 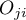 to liczności symetrycznych par w tabeli
to liczności symetrycznych par w tabeli 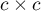
Statystyka testowa ma postać:
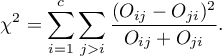
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z liczbą stopni swobody wyliczaną według wzoru 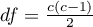 .
.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

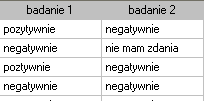
Przeprowadzono 2 badania opinii studentów na temat określonego wykładowcy akademickiego. Oba badania pozwalały ocenić wykładowcę negatywnie, pozytywnie, lub wybrać odpowiedź neutralną - nie mam zdania. Oba badania przeprowadzono na tej samej próbie 250 studentów z tym, że pierwsze badanie dokonano dzień przed egzaminem z przedmiotu prowadzonego przez ocenianego wykładowcę a drugie dzień po egzaminie. Poniżej przedstawiono fragment danych w postaci surowej oraz całość danych w postaci tabeli kontyngencji. Chcemy zbadać, czy obydwa badania dają podobne wyniki.

Hipotezy:

gdzie np. zmiana opinii z pozytywnej na negatywną jest symetryczna względem zmiany opinii z negatywnej na pozytywną.
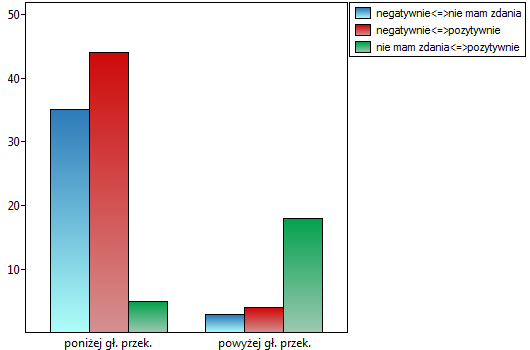
Porównując wartość  dla testu Bowkera
dla testu Bowkera 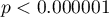 z poziomem istotności
z poziomem istotności  stwierdzamy, że opinie studentów zmieniły się. Z tabeli wynika, że istotnie więcej było tych studentów, którzy zmienili swoją opinię na negatywną po egzaminie niż tych którzy zmienili ją na pozytywną, oraz wielu studentów oceniających przed egzaminem wykładowcę pozytywnie po egzaminie nie wyrażało już takiego zdania.
stwierdzamy, że opinie studentów zmieniły się. Z tabeli wynika, że istotnie więcej było tych studentów, którzy zmienili swoją opinię na negatywną po egzaminie niż tych którzy zmienili ją na pozytywną, oraz wielu studentów oceniających przed egzaminem wykładowcę pozytywnie po egzaminie nie wyrażało już takiego zdania.
Gdybyśmy ograniczyli nasze badanie do osób mających zdefiniowany pogląd na temat wykładowcy (tzn. oceniają tylko pozytywnie lub negatywnie), to moglibyśmy wykorzystać test McNemara:
Hipotezy:

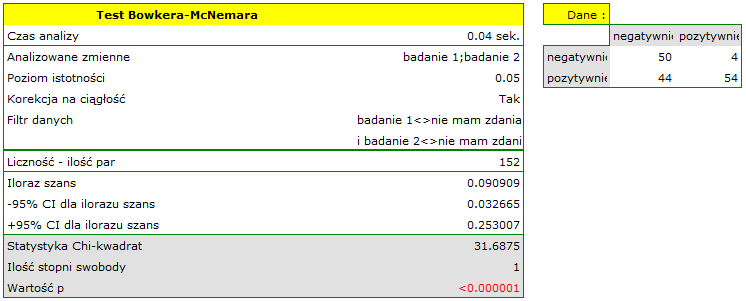
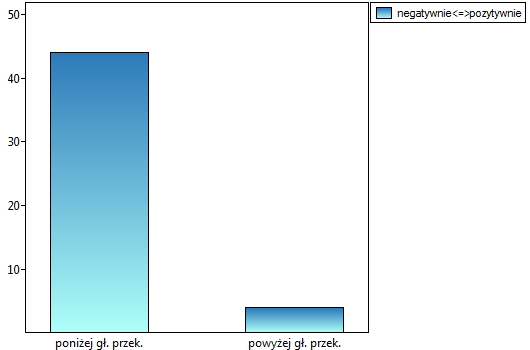
Porównując wartość  dla testu McNemara
dla testu McNemara 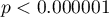 z poziomem istotności
z poziomem istotności  stwierdzamy, że opinie studentów zmieniły się. Istotnie więcej było tych studentów, którzy zmienili swoją opinie na negatywną po egzaminie niż tych którzy zmienili ją na pozytywną. Szansa zmiany opinii z pozytywnej (przed egzaminem) na negatywną (po egzaminie) jest jedenaście
stwierdzamy, że opinie studentów zmieniły się. Istotnie więcej było tych studentów, którzy zmienili swoją opinie na negatywną po egzaminie niż tych którzy zmienili ją na pozytywną. Szansa zmiany opinii z pozytywnej (przed egzaminem) na negatywną (po egzaminie) jest jedenaście 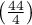 razy większa niż z negatywnej na pozytywną (szansa zmiany opinii w przeciwną stronę to:
razy większa niż z negatywnej na pozytywną (szansa zmiany opinii w przeciwną stronę to: 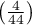 czyli 0.090909).
czyli 0.090909).
1)
McNemar Q. (1947), Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika, 12, 153-157
2)
Rufibach K. (2010), Assessment of paired binary data; Skeletal Radiology volume 40, pages1–4
3)
Fagerland M.W., Lydersen S., and Laake P. (2013), The McNemar test for binary matched-pairs data: mid-p and asymptotic are better than exact conditional, BMC Med Res Methodol; 13: 91
4)
Liddell F.D.K. (1983), Simplified exact analysis of case-referent studies; matched pairs; dichotomous exposure. Journal of Epidemiology and Community Health; 37:82-84
5)
Bowker A.H. (1948), Test for symmetry in contingency tables. Journal of the American Statistical Association, 43, 572-574
statpqpl/porown2grpl/nparpl/mcnemarrpl.txt · ostatnio zmienione: 2022/09/26 22:21 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

