Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:plotpl:mackorel
Macierze korelacji
Kiedy interesuje nas korelacja pomiędzy wieloma zmiennymi, wygodnym sposobem jej zobrazowania jest przedstawienie współczynników korelacji w postaci tabeli. W zależności od skali na jakiej zebrano dane, w programie PQStat mamy do wyboru współczynniki:
- r-Pearsona (skala interwałowa)
- r-Spearmana (skala porządkowa lub silniejsza)
- tau-Kendalla (skala porządkowa lub silniejsza)
- C-Pearsona (skala nominalna lub silniejsza)
- V-Cramera (skala nominalna lub silniejsza)
- Phi (skala nominalna lub silniejsza)
- Q-Yulea (skala nominalna lub silniejsza)
W wyniku analizy powstają dwie macierze, tzn. macierz współczynników korelacji i macierz wartości p dla testu określającego istotność statystyczną danego współczynnika (dla włóczników r-Pearsona, r-Pearsona i tau-Kendalla były to dedykowane im testy, dla skali nominalnej test chi-kwadrat). W macierzy współczynników korelacji , w miejscu przecięcia się dwóch zmiennych podany jest współczynnik ich korelacji, a jego wartość p znajduje się w odpowiadającym mu miejscu w drugiej macierzy. Kolor komórki w macierzy współczynników jest stopniowany od niebieskiego (ujemne współczynniki) do czerwonego (dodatnie współczynniki).
Analiza wyznacza korelację dla każdej pary zmiennych, dlatego braki danych pomijane są parami. Jeśli chcemy przeprowadzić analizę pomijając barki danych występujące w innych zmiennych (tzn. nie tych, które wchodzą w skald danej pary), wówczas powinniśmy to zrobić korzystając z filtru zaawansowanego.
Okno z ustawieniami opcji macierzy korelacji wywołujemy poprzez Statystyki→Kalkulatory→Macierze korelacji
Okno z ustawieniami opcji wykresu macierzowego dla macierzy korelacji wywołujemy poprzez Wykresy→Wykres macierzowy
Przykład (plik markery inne.pqs)
Przedstawiono fragment większego badania dotyczącego choroby nowotworowej. Zabrane dane dotyczą grupy 100 osób. W badaniu mierzono min. wartości markerów nowotworowych (skala interwałowa), wyznaczono kategorie BMI dla pacjentów oraz pytano o opinie na temat możliwego wpływu miejsca zamieszkana oraz diety na zdrowie (skala porządkowa), zanotowano też odpowiedzi pacjentów na temat palenia przez nich papierosów, spożywania alkoholu oraz rodzaju wykonywanej pracy (skala nominalna).
Prowadzenie analiz wielowymiarowych często zakłada konieczność wcześniejszego sprawdzenia wzajemnych korelacji zmiennych. Na potrzeby dalszych analiz:
(1) Sprawdzimy korelację wewnątrz każdej z tych grup.
(2) Sprawdzimy korelację między wszystkimi zmiennymi.
(1)
Dla skali interwałowej, przy założeniu normalności rozkładu korelację możemy sprawdzić współczynnikiem korelacji liniowej Pearsona. Najsilniejsza korelacja dotyczy markera A i markera C (r=0.8995, p<0.0001) najsłabsza i nieistotna statystycznie dotyczy markera B i markera C (r=0.0753, p=0.4567).
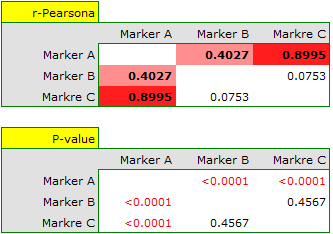
Opisane korelacje można obserwować na wykresach rozrzutu (oś X tych wykresów to zmienna opisana w kolumnach, oś Y w wierszach), a rozkłady poszczególnych zmiennych na wykresach kolumnowych.
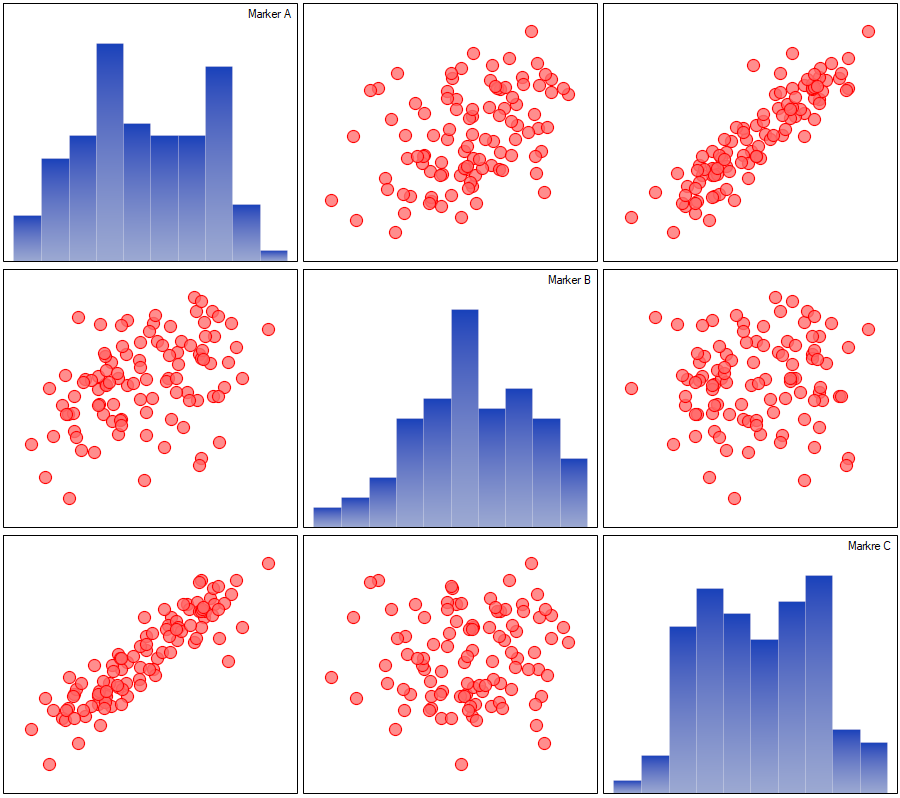
Dla skali porządkowej korelację sprawdzimy przy pomocy współczynnika korelacji Spearmana. Jedyna istotna korelacja dotyczy diety i miejsca zamieszkania (r=0.2634, p=0.0081)
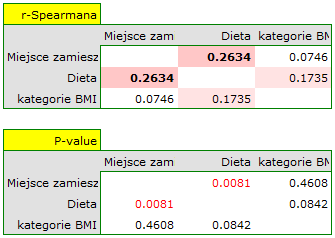
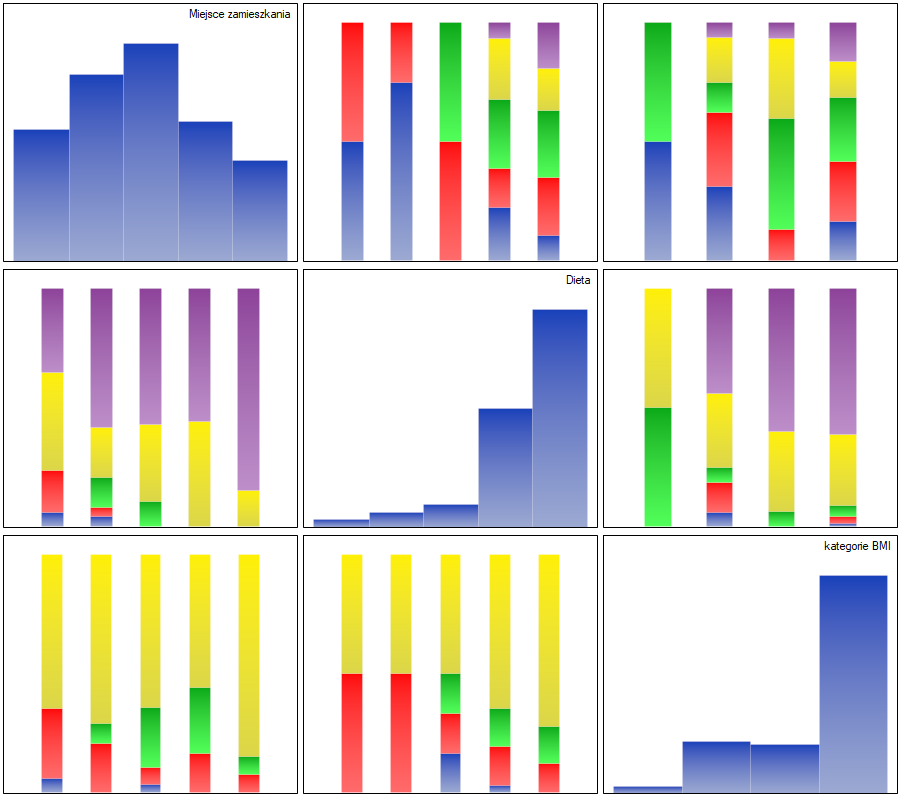
Opisane korelacje można obserwować na wykresach kolumnowych skumulowanych (oś X tych wykresów to zmienna opisana w kolumnach, legenda to zmienna opisana w wierszach), a rozkłady poszczególnych zmiennych na wykresach kolumnowych znajdujących się na głównej przekątnej.
Dla skali nominalnej korelację sprawdzimy przy pomocy współczynnika C-Pearsona skorygowanego na wielkość tabeli. Nie uzyskaliśmy istotnych statystycznie korelacji.
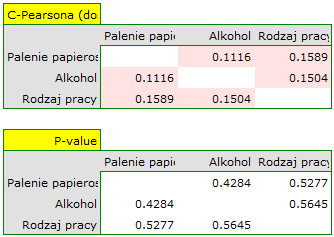
Ewentualne korelacje można obserwować na wykresach kolumnowych skumulowanych (oś X tych wykresów to zmienna opisana w kolumnach, legenda to zmienna opisana w wierszach), a rozkłady poszczególnych zmiennych na wykresach kolumnowych znajdujących się na głównej przekątnej.
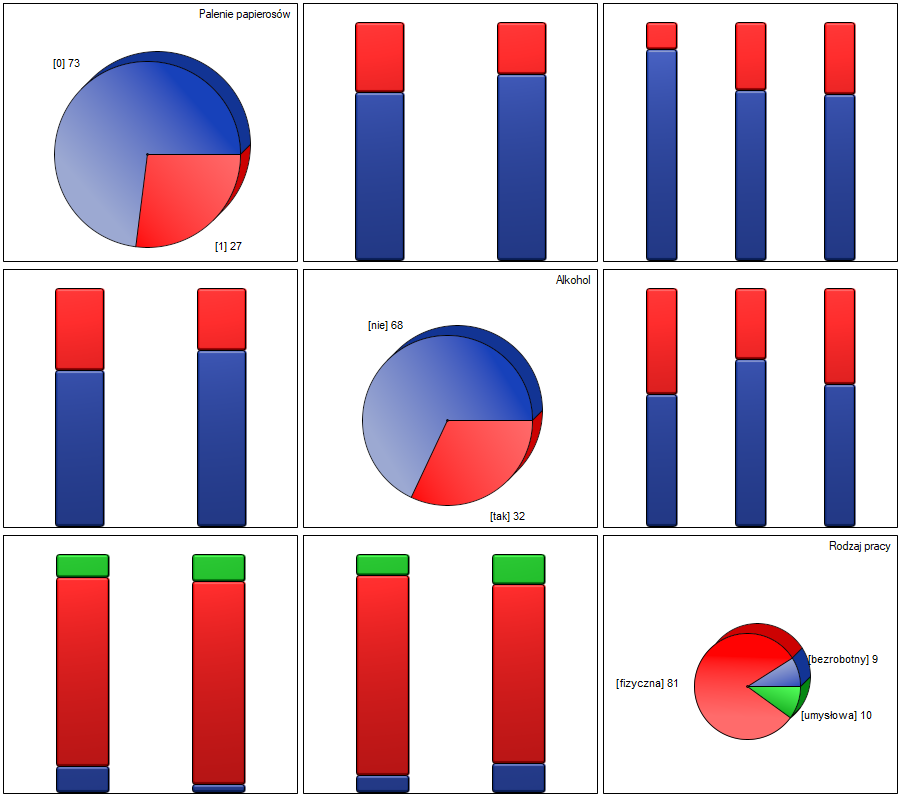
(2) Najłatwiejszym sposobem wyznaczania korelacji pomiędzy zmiennymi mierzonymi na różnych skalach jest sprowadzenie ich do tej samej skali. W tym celu zapiszemy dane interwałowe dzieląc je na dwie kategorie niski i wysoki np. wg kwantyli. Możemy to z robić automatycznie w oknie transformacji poprzez menu Dane→Transformuj.
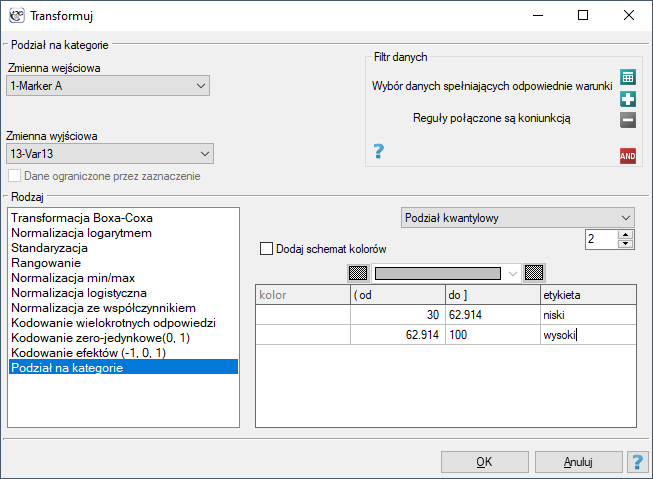
Dane iporządkowe również podzielimy na dwie kategorie, ale podziału dokonamy wybierając Właściwości zmiennych (kody/etykiety) w oknie analizy poprzez menu kontekstowe (prawy klawisz myszy) i wpisując tylko dwie obowiązujące wartości i dwie etykiety.
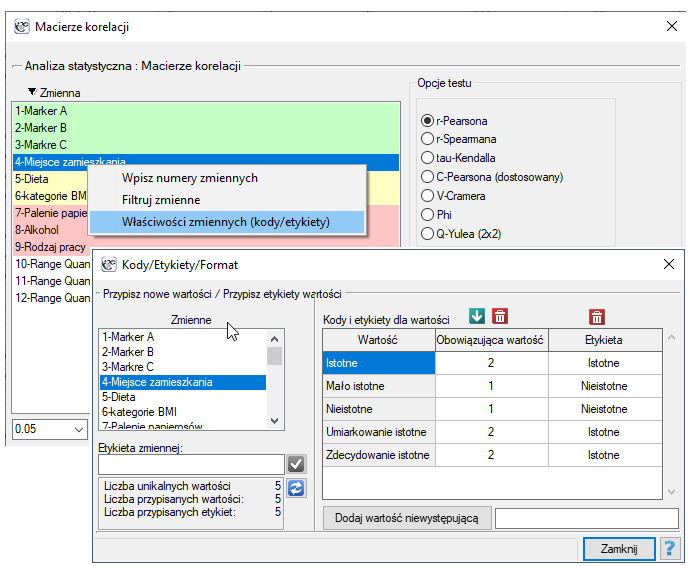
W wyniku przedstawimy tylko macierz korelacji (bez wykresu), ponieważ wykres dla tak wielu zmiennych nie będzie wystarczająco czytelny.
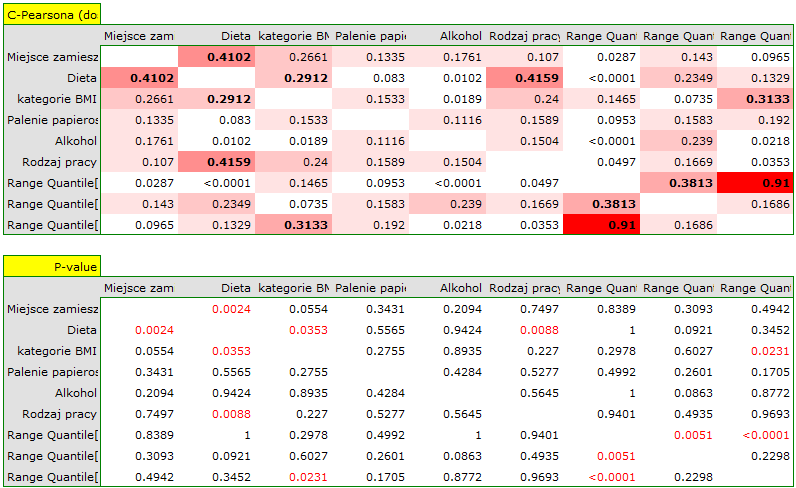
statpqpl/plotpl/mackorel.txt · ostatnio zmienione: 2021/02/04 22:10 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


