Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Analiza przestrzenna » Analiza gęstości » Metoda kwadratów
Pasek boczny
przestrzenpl:gestoscpl:kwadratypl
Metoda kwadratów
Metoda kwadratów (ang. Quadrat Count Methods).
Graficznie metoda ta jest uogólnieniem histogramu, czy analizy jednowymiarowej, na przypadek dwuwymiarowy. Budując histogram dysponujemy jedną zmienną, którą dzielimy na przedziały równej długości i podajemy liczbę przypadków w każdym przedziale. Budując siatkę kwadratów dysponujemy dwiema zmiennymi, na podstawie których budujemy siatkę i podajemy liczbę przypadków w każdym kwadracie siatki (DPS - ang. Dot Per Square). Stosunek tej liczności do pola kwadratu stanowi o intensywność barwy na jaką kolorowany jest dany kwadrat siatki.
![LaTeX \begin{tabular}{|l|l|l|l|}
\hline
\cellcolor[rgb]{0.8,0.8,0.8}&\textcolor[rgb]{1,1,1}{aaa}&\cellcolor[rgb]{0.4,0.4,0.4}\textcolor[rgb]{0.4,0.4,0.4}{aa}$\bullet$&\textcolor[rgb]{1,1,1}{aaa}\\
\cellcolor[rgb]{0.8,0.8,0.8}$\bullet$&&\cellcolor[rgb]{0.4,0.4,0.4}$\bullet$&\\ \hline
\textcolor[rgb]{1,1,1}{aaa}&\textcolor[rgb]{1,1,1}{aaa}&\textcolor[rgb]{1,1,1}{aaa}&\textcolor[rgb]{0.8,0.8,0.8}{aa}\cellcolor[rgb]{0.8,0.8,0.8}$\bullet$\\
\textcolor[rgb]{1,1,1}{aaa}&\textcolor[rgb]{1,1,1}{aaa}&\textcolor[rgb]{1,1,1}{aaa}&\cellcolor[rgb]{0.8,0.8,0.8}\\ \hline
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img43a14f7bd3863948a5edc027448c7e7b.png)
Na podstawie liczby przypadków w kwadratach siatki możemy badać ich rozkład przestrzenny. Jeśli w każdym kwadracie znajduje się taka sama liczba punktów, oznacza to idealnie równomierny rozkład. Gdy jest odwrotnie, gdy zróżnicowanie liczby punków w kwadratach jest bardzo duże, oznacza to że są kwadraty o znacznie większej liczbie punktów, czyli tworzą się klastery.
Jeśli przez  oznaczymy liczbę punktów badanego obszaru, a przez
oznaczymy liczbę punktów badanego obszaru, a przez 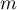 liczbę kwadratów na jaki badany obszar zostaje podzielony, wówczas można wyznaczyć średnią, wariancję i odchylenie standardowe liczby punktów na kwadrat:
liczbę kwadratów na jaki badany obszar zostaje podzielony, wówczas można wyznaczyć średnią, wariancję i odchylenie standardowe liczby punktów na kwadrat:
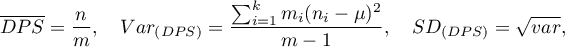 gdzie
gdzie 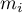 - to liczba kwadratów z liczbą punktów równą
- to liczba kwadratów z liczbą punktów równą 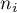 .
.
Współczynnik 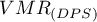
Najważniejszą informacje niesie współczynnik będący ilorazem wariancji i średniej (ang. variance-mean ratio):
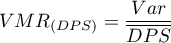 Wartość
Wartość 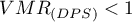 wskazuje na zbyt małe zróżnicowanie liczby punktów w kwadratach co sugeruje efekt równomiernego rozproszenia,
wskazuje na zbyt małe zróżnicowanie liczby punktów w kwadratach co sugeruje efekt równomiernego rozproszenia, 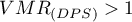 oznacza zbyt duże zróżnicowanie liczby punktów w kwadratach a więc efekt klasteryzacji, a wartość bliska 1 wskazuje na przeciętne zróżnicowanie liczby punktów w kwadratach co oznacza losowość rozkładu punktów.
oznacza zbyt duże zróżnicowanie liczby punktów w kwadratach a więc efekt klasteryzacji, a wartość bliska 1 wskazuje na przeciętne zróżnicowanie liczby punktów w kwadratach co oznacza losowość rozkładu punktów.
W literaturze często rozważany jest wskaźnik wielkości klasterów (ang. Index of Cluster Size - ICS):
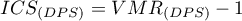 Oczekiwana wartość
Oczekiwana wartość 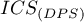 przy założeniu losowości punktów wynosi 0. Wartość dodatnia wskazuje na efekt klasteryzacji, a ujemna na regularny rozkład punktów.
przy założeniu losowości punktów wynosi 0. Wartość dodatnia wskazuje na efekt klasteryzacji, a ujemna na regularny rozkład punktów.
Istotności współczynnika 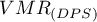
Test sprawdzający istotność współczynnika 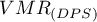 służy do weryfikacji hipotezy o tym, że obserwowane liczności punktów w kwadratach są takie same jak oczekiwane liczności, które pojawiłyby się dla losowego rozkładu punktów.
służy do weryfikacji hipotezy o tym, że obserwowane liczności punktów w kwadratach są takie same jak oczekiwane liczności, które pojawiłyby się dla losowego rozkładu punktów.
Hipotezy:
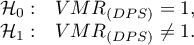
Statystyka testowa ma postać:
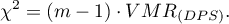 Statystyka ta ma asymptotycznie rozkład chi-kwadrat z
Statystyka ta ma asymptotycznie rozkład chi-kwadrat z 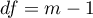 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Uwaga!
Uzyskany wynik analizy w znacznym stopniu zależy od gęstości siatki a więc od liczby/wielkości kwadratów na jakie dzielony jest analizowany obszar. W oknie opcji testu można ustawić siatkę, jaka będzie użyta do podziału badanego obszaru na kwadraty, podając liczbę kwadratów w pionie i w poziomie.
Okno z ustawieniami opcji metody kwadratów wywołujemy poprzez menu Analiza przestrzenna→Statystyki przestrzenne→Metoda kwadratów
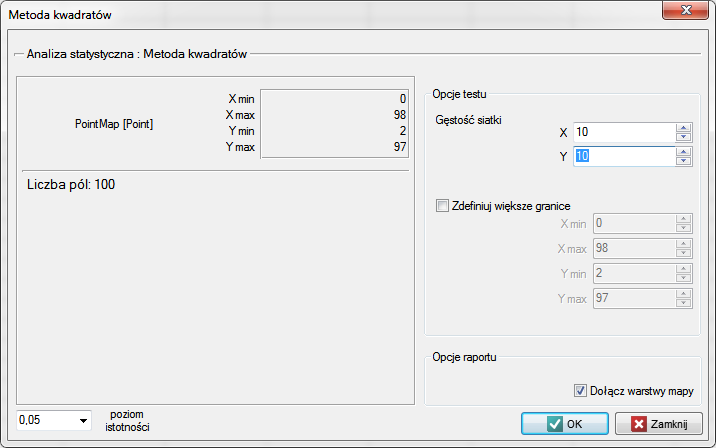
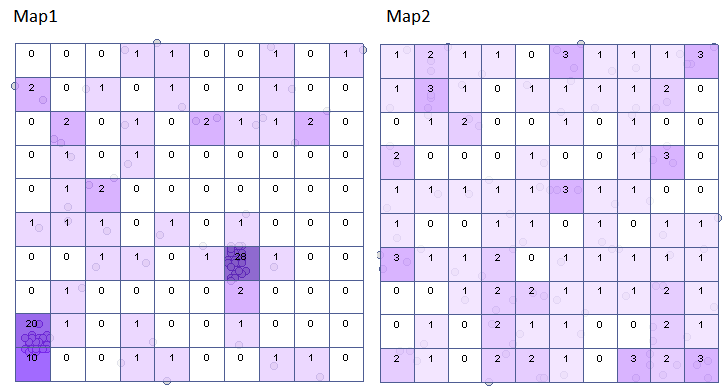
Na podstawie arkusza danych wygeneruj dwie mapy punktów i wykonaj analizę gęstości tych punktów. Odpowiedz na pytanie: Czy punkty są rozłożone losowo w każdej z tych map?
Mapy punktów tworzymy przy pomocy formuł: menu Dane→Formuły…
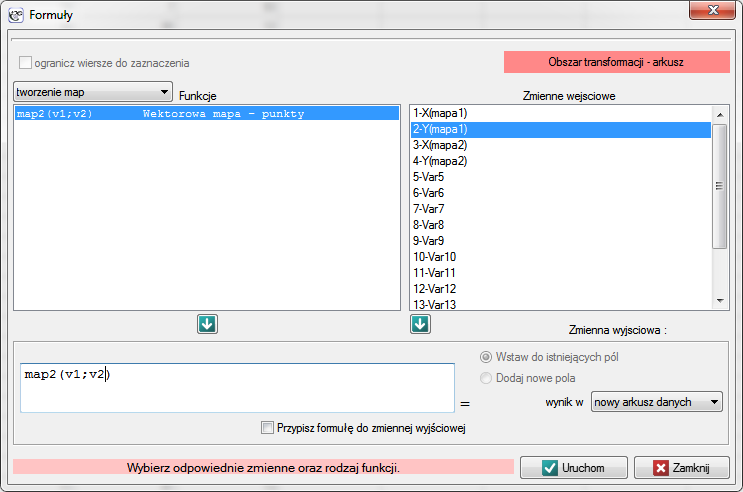
W rezultacie uzyskamy dwa nowe arkusze zawierające mapy. Dla każdego z tych arkuszy przeprowadzamy analizę kwadratów.
Hipotezy:
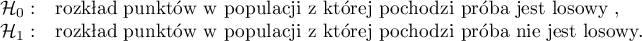
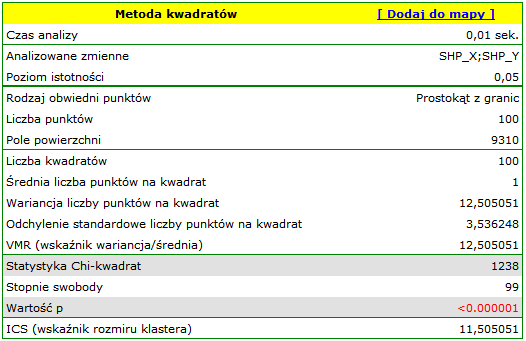
Wyniki dla mapy 1 wskazują na znaczne zróżnicowanie liczby punktów w kwadratach, czyli na efekt klasteryzacji (wartość 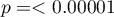 ). Efekt ten utrzymuje się dla różnych gęstości siatki. Dla siatki gęstości 10:10 współczynnik
). Efekt ten utrzymuje się dla różnych gęstości siatki. Dla siatki gęstości 10:10 współczynnik 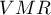 wynosi aż 12.5, cały raport został zamieszczony poniżej:
wynosi aż 12.5, cały raport został zamieszczony poniżej:
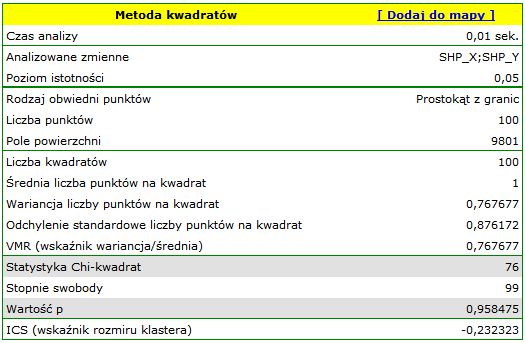
Dla mapy 2 sytuacja jest zupełnie inna. Dla siatki gęstości 10:10 mamy brak istotności statystycznej (wartość 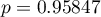 ) oraz wartość współczynnika
) oraz wartość współczynnika 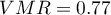 wskazują na losowość rozkładu punktów.
wskazują na losowość rozkładu punktów.
Wykorzystując przycisk  umieszczony w raporcie przenosimy się do Menadżera map by z wyświetlonej listy warstw wybrać wykonaną siatkę analizy kwadratów i uzyskać graficzną interpretację wyników.
umieszczony w raporcie przenosimy się do Menadżera map by z wyświetlonej listy warstw wybrać wykonaną siatkę analizy kwadratów i uzyskać graficzną interpretację wyników.
przestrzenpl/gestoscpl/kwadratypl.txt · ostatnio zmienione: 2014/12/20 23:57 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

