PQStat - Baza Wiedzy

Spis treści

Jądrowy estymator gęstości
- Dwuwymiarowy estymator jądrowy
- Trójwymiarowy estymator jądrowy

Jądrowy estymator gęstości

Dwuwymiarowy estymator jądrowy

Dwuwymiarowy estymator jądrowy (podobnie jak estymator jednowymiarowy) pozwala na przybliżenie rozkładu danych, wyrażonego metodą kwadratów, poprzez wygładzenie.

Dwuwymiarowy jądrowy estymator gęstości przybliża gęstość rozkładu danych tworząc wygładzoną płaszczyznę gęstości w sposób nieparametryczny. Dzięki niemu uzyskuje się lepszą estymację gęstości niż daje tradycyjna metoda kwadratów, której kwadraty tworzą funkcję schodkową. Tak jak w przypadku jednowymiarowym estymator ten definiowany jest w oparciu o odpowiednio wygładzone zsumowane funkcje jądra (patrz opis w Podręczniku Użytkownika PQStat). Do wyboru mamy kilka sposobów wygładzania oraz kilka funkcji jądra opisanych dla estymatora jednowymiarowego (Gaussa, jednostajna, trójkątna, Epanechnikova, quartic/biweight). O ile funkcja jądra nie ma dużego wpływu na uzyskane wygładzenie płaszczyzny, o tyle współczynnik wygładzania tak.

Dla każdego punktu 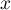$x$ z zakresu określonego przez dane wyznacza się gęstość czyli estymator jądrowy. Powstaje on poprzez zsumowanie iloczynu wartości funkcji jąder w tym punkcie:

$\begin{displaymath} \hat{f}_K(x,y)=\frac{1}{n}\sum_{i=1}^nK_h(t_i)K_h(s_i) \end{displaymath}$

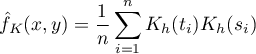
Jeśli poszczególnym przypadkom nadamy wagi 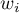$w_i$ , wówczas możemy zbudować ważony jądrowy estymator gęstości definiowany wzorem:

$\begin{displaymath} \hat{f}_K(x,y)=\frac{1}{\sum_{i=1}^nw_i}\sum_{i=1}^nw_iK_h(t_i)K_h(s_i) \end{displaymath}$

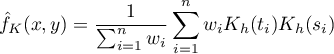
Okno z ustawieniami opcji jądrowego estymatora gęstości 2D wywołujemy poprzez menu Analiza przestrzenna→Statystyki przestrzenne→Jądrowy estymator gęstości 2D

Przykład c.d. (plik snow.pqs)

Obecnie zasadniczym problemem w przedstawianiu danych punktowych dotyczących lokalizacji osób jest konieczność ich ochrony. Ochrona danych osobowych zabrania takiego publikowania wyników badań, by na ich podstawie można było rozpoznać daną osobę, nie można więc m.in. publikować mapy w postaci punktów z zaznaczonym miejscem zamieszkania. Dobrym rozwiązaniem w takim przypadku jest estymator gęstości punktów.

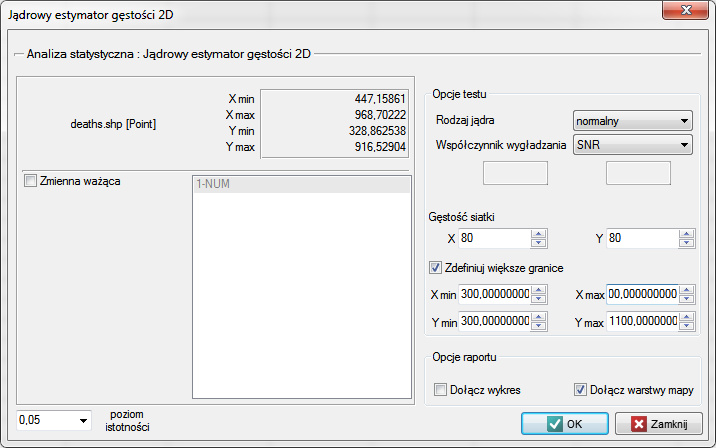
Przedstawimy dane punktowe obrazujące epidemię cholery w Londynie w roku 1854 przy pomocy takiego estymatora. W tym celu posłużymy się mapą punktów (śmierci z powodu cholery) z nałożonymi już warstwami ilustrującymi zarówno ulice jak i pompy wodne oraz wynik analizy lekarza Johna Snow.

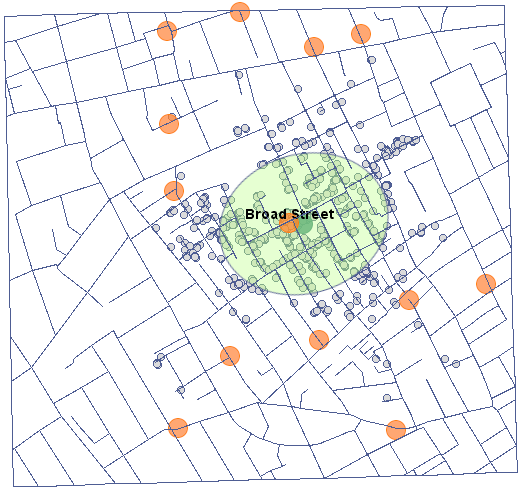
W oknie analizy dla mapy punktów pozostaniemy przy jądrze rozkładu Gauss'a (normalnego) i współczynniku wygładzania SNR. Gęstość siatki ustawimy na 80:80. Granice zwiększymy tak, by brzegi nie odznaczały się ostrą krawędzią wpisując 300 jako wartość minimalną współrzędnej X i Y oraz 1100 jako wartość maksymalną.

Korzystając z przycisku umieszczonego w raporcie udajemy się do Menadżera map, gdzie możemy dodać warstwę przedstawiającą ten estymator (ostatnia pozycja z listy warstw).

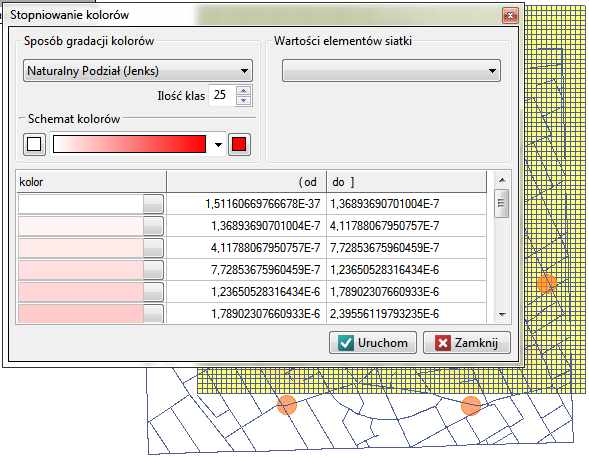
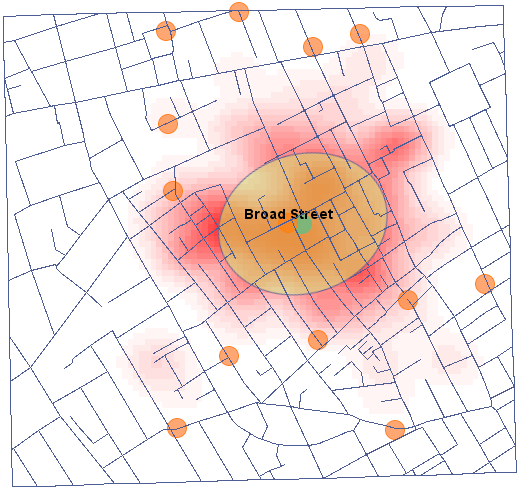
Po nałożeniu warstwy jądrowego estymatora gęstości należy go edytować by usunąć linie siatki i zmienić kolor żółty na naturalny kolor tła (w tym przypadku biały). Tak uzyskaną warstwę przenosimy w górę , tak by została wyrysowana na początku. Warstwę punktów (Mapa bazowa) wyłączamy.

Przykład c.d. (plik kwadraty.pqs)

Przy pomocy estymatora jądrowego przedstawimy gęstość punktów dla mapy 1 - uzyskanej we wcześniejszej części zadania.

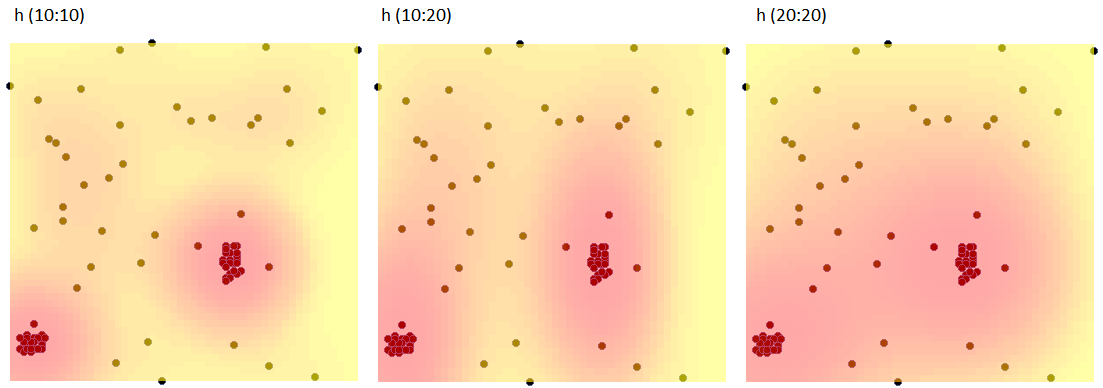
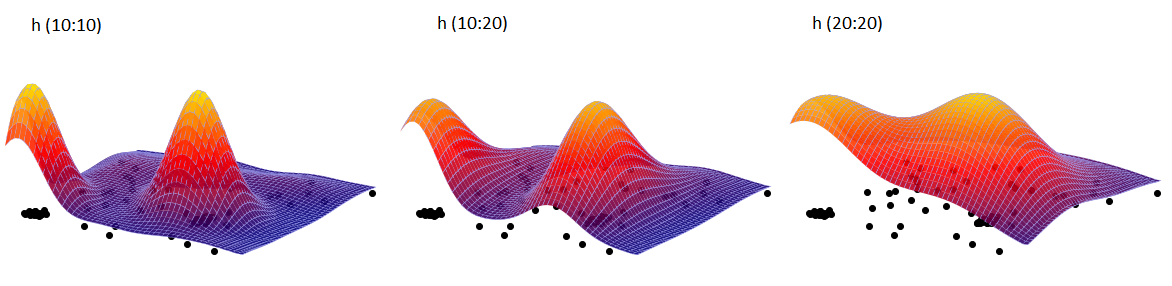
W oknie analizy ustawiamy gęstość siatki na 50:50 i typ jądra jako rozkład normalny oraz dołączamy wykres. Wykonujemy analizę trzy razy zmieniając przy tym współczynnik wygładzania Użytkownika: h (10:10), następnie h (10:20) i h (20:20). Uzyskane wyniki zaprezentowane na mapie (poprzez Menadżer map) i na wykresie 3D przedstawiono poniżej:

Trójwymiarowy estymator jądrowy

Trójwymiarowy estymator jądrowy (podobnie jak estymator jednowymiarowy i estymator dwuwymiarowy) pozwala na przybliżenie rozkładu danych poprzez ich wygładzenie.

Trójwymiarowy jądrowy estymator gęstości przybliża gęstość rozkładu danych tworząc wygładzoną płaszczyznę gęstości w sposób nieparametryczny. Graficznie możemy go przedstawić wyrysowując dwa pierwsze wymiary w warstwach stworzonych przez wymiar trzeci. Tak jak w przypadku jednowymiarowym (patrz opis w Podręczniku Użytkownika PQStat) i dwuwymiarowym estymator ten definiowany jest w oparciu o odpowiednio wygładzone zsumowane funkcje jądra. Do wyboru mamy kilka sposobów wygładzania oraz kilka funkcji jądra opisanych dla estymatora jednowymiarowego (Gaussa, jednostajna, trójkątna, Epanechnikova, quartic/biweight). O ile funkcja jądra nie ma dużego wpływu na uzyskane wygładzenie płaszczyzny, o tyle współczynnik wygładzania tak.

Dla każdego punktu 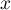$x$ z zakresu określonego przez dane wyznacza się gęstość czyli estymator jądrowy. Powstaje on poprzez zsumowanie iloczynu wartości funkcji jąder w tym punkcie:

$\begin{displaymath} \hat{f}_K(x,y,z)=\frac{1}{n}\sum_{i=1}^nK_h(t_i)K_h(s_i)K_h(r_i) \end{displaymath}$

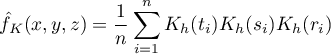
Jeśli poszczególnym przypadkom nadamy wagi 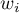$w_i$ , wówczas możemy zbudować ważony jądrowy estymator gęstości definiowany wzorem:

$\begin{displaymath} \hat{f}_K(x,y,z)=\frac{1}{\sum_{i=1}^nw_i}\sum_{i=1}^nw_iK_h(t_i)K_h(s_i)K_h(r_i) \end{displaymath}$

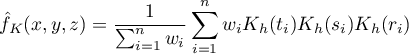
Okno z ustawieniami opcji jądrowego estymatora gęstości 3D wywołujemy poprzez menu Analiza przestrzenna→Statystyki przestrzenne→Jądrowy estymator gęstości 3D

Uwaga!

Wyświetlanie kolejnych warstw estymatora, wyznaczonych przez trzeci wymiar, możliwe jest w poprzez edycję warstwy w oknie menadżera map i wybranie odpowiedniego indeksu warstwy.

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Spis treści

Jądrowy estymator gęstości

Dwuwymiarowy estymator jądrowy

Trójwymiarowy estymator jądrowy

Narzędzia strony