Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
przestrzenpl:autocorpl:ggarypl
Statystyka globalna Gearego
Podobnie jak analiza Morana statystyka globalna Gearego bada stopień intensywności danej cechy w obiektach przestrzennych.
Uwaga!
Nie zaleca się przeprowadzania analizy Gearego dla obiektów nie posiadających sąsiedztwa (obiektów opisanych w macierzy wag wyłącznie wartością 0). Obiekty takie można wykluczyć z analizy dezaktywując je (Rozdział Ograniczenie obszaru roboczego), lub przeprowadzić analizę wybierając inny sposób definiowania sąsiedztwa (inną macierz wag).
Współczynnik autokorelacji Gearego – wprowadzony przez Gearego w roku 19541).
Jest jedną z możliwych alternatyw dla statystyki globalnej Morana. Podobnie jak analiza Morana bada ona stopień intensywności danej cech  w obiektach przestrzennych opisanych za pomocą macierzy wag o elementach
w obiektach przestrzennych opisanych za pomocą macierzy wag o elementach 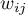 . Tym razem zamiast wyliczania sumy iloczynów :
. Tym razem zamiast wyliczania sumy iloczynów : 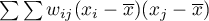 wyliczana jest suma kwadratów różnic:
wyliczana jest suma kwadratów różnic:
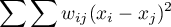
W rezultacie współczynnik autokorelacji Gearego wyraża się wzorem:
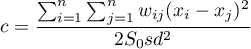
gdzie:
 – liczba obiektów przestrzennych (liczba punktów lub wielokątów),
– liczba obiektów przestrzennych (liczba punktów lub wielokątów),
 ,
, 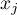 – to wartości zmiennej dla porównywanych obiektów,
– to wartości zmiennej dla porównywanych obiektów,
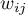 – elementy przestrzennej macierzy wag (macierz wag standaryzowana rzędami do jedynki),
– elementy przestrzennej macierzy wag (macierz wag standaryzowana rzędami do jedynki),
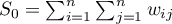 ,
,
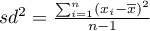 – wariancja,
– wariancja,
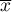 – to średnia wartość zmiennej dla wszystkich obiektów.
– to średnia wartość zmiennej dla wszystkich obiektów.
Interpretacja współczynnika Gearego:
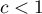 i
i 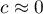 oznacza występowanie klasterów podobnych wartości – dodatnią autokorelację;
oznacza występowanie klasterów podobnych wartości – dodatnią autokorelację;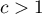 oznacza występowanie tzw. hot spots czyli zdecydowanie różnych wartości w obszarach sąsiedzkich – ujemną autokorelację;
oznacza występowanie tzw. hot spots czyli zdecydowanie różnych wartości w obszarach sąsiedzkich – ujemną autokorelację;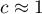 oznacza losowe rozłożenie się badanej wartości w przestrzeni – brak autokorelacji.
oznacza losowe rozłożenie się badanej wartości w przestrzeni – brak autokorelacji.
Uwaga!
Gdy wartości badanej cechy charakteryzuje duża zmienność wariancji, wówczas pożądane jest jej ustabilizowanie. Podstawowe informacje na temat wygładzania zmiennych zostały opisane w rozdziale Wygładzanie przestrzenne zmiennej
Istotności współczynnika autokorelacji Gearego
Test do sprawdzania istotności współczynnika autokorelacji Gearego służy do weryfikacji hipotezy o braku autokorelacji przestrzennej.
Hipotezy:
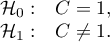
Statystyka testowa ma postać:
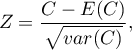
gdzie:
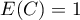 – wartość oczekiwana,
– wartość oczekiwana,
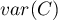 – wariancja.
– wariancja.
W zależności od założenia dotyczącego rozkładu populacji, z której pochodzi próba, wybierany jest sposób wyznaczania wariancji (Cliff i Ord (1981)2), oraz Goodchild (1986)3)). Jeśli jest to rozkład normalny, wówczas:
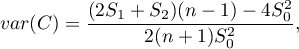
gdzie:
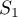 i
i 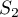 zdefiniowane są jak dla analizy Morana.
zdefiniowane są jak dla analizy Morana.
Jeśli rozkład jest losowy, wówczas:
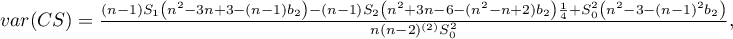
gdzie:
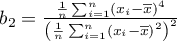 ,
,
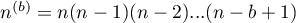 .
.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wartość  , wyznaczoną na podstawie statystyki testowej, porównujemy z poziomem istotności
, wyznaczoną na podstawie statystyki testowej, porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji analizy Gearego wywołujemy poprzez menu Analiza przestrzenna → Statystyki przestrzenne → Statystyka globalna C Gearego.
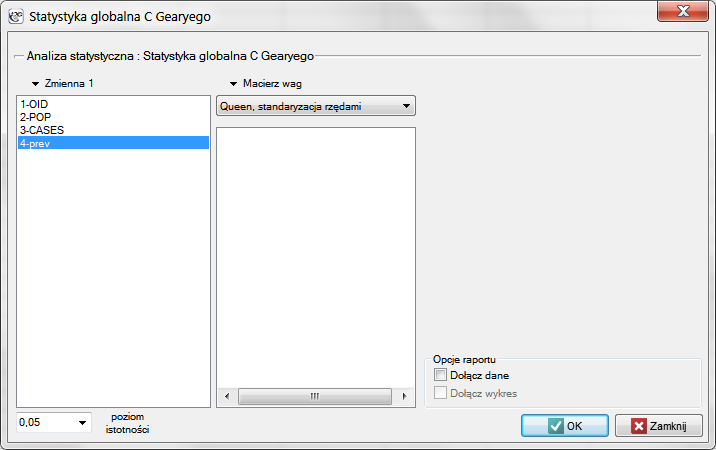
Przykład c.d. (katalog: leukemia, plik: leukemia)
Analizie poddamy dane dotyczące białaczki.
- Mapa
leukemiazawiera informacje o lokalizacji 281 wielokątów (regionów spisowych (ang.census tracts)) w północnej części stanu New York. - Dane do mapy
leukemia:- Kolumna
CASES– liczba przypadków białaczki w latach 1978-1982 przypisana do poszczególnych obiektów (regionów spisowych). Wartość ta powinna być liczbą całkowitą, tu jednak, zgodnie z opisem Wallera (1994) część przypadków, która nie mogła zostać obiektywnie przypisana do konkretnego regionu, została podzielona proporcjonalnie. Stąd liczności przypadków przypisanych do 281 obiektów nie są liczbami całkowitymi. - Kolumna
POP– liczność populacji w poszczególnych obiektach. - Kolumna
prev– współczynnik częstości występowania białaczki na 100000 osób, dla każdego obiektu w jednym roku: prev=(CASES/POP)*100000/5
Analiza globalna Morana wskazała na brak autokorelacji przestrzennej. Tym razem, by sprawdzić, czy na badanym obszarze północnej części stanu New York możliwe jest zlokalizowanie klasterów białaczki, wyliczymy globalną statystykę C Gearego.
Zaczynamy od przedstawienia rozkładu geograficznego współczynnika częstości (prev) na mapie zgodnie z wartościami zmiennej prev dzieląc ją na kwartyle:
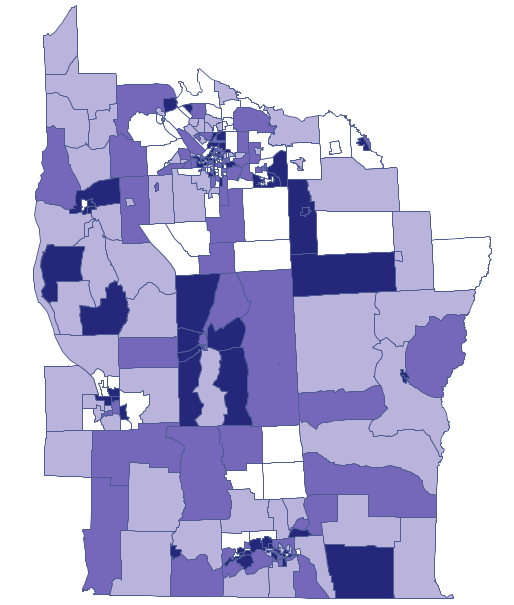
Kolory ciemne na mapie obrazują miejsca o wyższym współczynniku częstości białaczki, miejsca jasne to niski współczynnik. Współczynnik korelacji Gearego uzyskany w analizie wynosi: 0.884986.
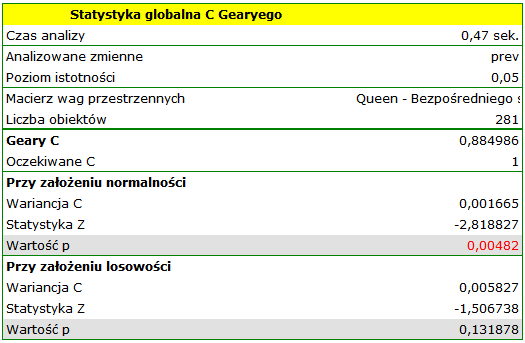
Uzyskany rezultat przy założeniu losowego rozkładu danych jest różny od wyniku uzyskanego przy założeniu rozkładu normalnego. Może to świadczyć o niestabilności wyników i być wskazaniem do dalszych analiz opartych na zmiennych wygładzonych.
przestrzenpl/autocorpl/ggarypl.txt · ostatnio zmienione: 2014/08/25 21:22 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

