Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Baza Wiedzy » statpqpl » Modele wielowymiarowe » Liniowa regresja wieloraka » Weryfikacja modelu
Pasek boczny
pl:statpqpl:wielowympl:wielorpl:weryfpl
Weryfikacja modelu
- Istotność statystyczna poszczególnych zmiennych w modelu.
Na podstawie współczynnika oraz jego błędu szacunku możemy wnioskować czy zmienna niezależna, dla której ten współczynnik został oszacowany wywiera istotny wpływ na zmienną zależną. W tym celu posługujemy się testem t-Studenta.
Hipotezy:
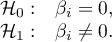
Wyliczmy statystykę testową według wzoru:
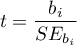
Statystyka testowa ma rozkład t-Studenta z 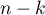 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

- Jakość zbudowanego modelu liniowej regresji wielorakiej możemy ocenić kilkoma miarami.
- Błąd standardowy estymacji - jest miarą dopasowania modelu:
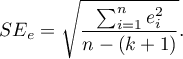
Miara ta opiera się na resztach modelu 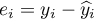 , czyli rozbieżności pomiędzy rzeczywistymi wartościami zmiennej zależnej
, czyli rozbieżności pomiędzy rzeczywistymi wartościami zmiennej zależnej 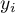 w próbie a wartościami zmiennej zależnej
w próbie a wartościami zmiennej zależnej 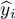 wyliczonej na podstawie zbudowanego modelu. Najlepiej byłoby, gdyby różnica ta była jak najbliższa zeru dla wszystkich badanych obiektów próby. Zatem, aby model był dobrze dopasowany, błąd standardowy estymacji (
wyliczonej na podstawie zbudowanego modelu. Najlepiej byłoby, gdyby różnica ta była jak najbliższa zeru dla wszystkich badanych obiektów próby. Zatem, aby model był dobrze dopasowany, błąd standardowy estymacji (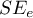 ) wyrażony jako wariancja
) wyrażony jako wariancja 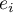 , powinien być jak najmniejszy.
, powinien być jak najmniejszy.
- Współczynnik korelacji wielorakiej
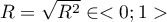 - określa siłę oddziaływania zespołu zmiennych
- określa siłę oddziaływania zespołu zmiennych 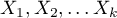 na zmienną zależną
na zmienną zależną  .
.
- Współczynnik determinacji wielorakiej
 - jest miarą dopasowania modelu.
- jest miarą dopasowania modelu.
Wartość tego współczynnika mieści się w przedziale 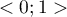 , gdzie 1 oznacza doskonałe dopasowanie modelu, 0 - zupełny bark dopasowania. W jego wyznaczeniu posługujemy się następującą równością:
, gdzie 1 oznacza doskonałe dopasowanie modelu, 0 - zupełny bark dopasowania. W jego wyznaczeniu posługujemy się następującą równością:
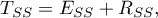
gdzie:
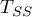 - całkowita suma kwadratów,
- całkowita suma kwadratów,
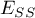 - suma kwadratów wyjaśniona przez model,
- suma kwadratów wyjaśniona przez model,
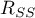 - resztowa suma kwadratów.
- resztowa suma kwadratów.
Współczynnik determinacji wyliczamy z wzoru:
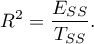
Wyraża on procent zmienności zmiennej zależnej tłumaczony przez model.
Ponieważ wartość współczynnika  zależy od dopasowania modelu, ale jest również wrażliwa na ilość zmiennych w modelu i liczność próby, bywają sytuacje, w których może być obarczona pewnym błędem. Dalego też wyznacza się poprawianą wartość tego parametru:
zależy od dopasowania modelu, ale jest również wrażliwa na ilość zmiennych w modelu i liczność próby, bywają sytuacje, w których może być obarczona pewnym błędem. Dalego też wyznacza się poprawianą wartość tego parametru:
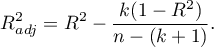
- Kryteria informacyjne opierają się na entropii informacji niesionej przez model (niepewności modelu) tzn. szacują utraconą informację, gdy dany model jest używany do opisu badanego zjawiska. Powinniśmy zatem wybierać model o minimalnej wartości danego kryterium informacyjnego.
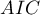 ,
, 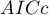 i
i 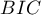 jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby zmiennych w modelu (
jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby zmiennych w modelu ( ) i liczności próby (
) i liczności próby ( ). W obu przypadkach element ten rośnie wraz ze wzrostem liczby zmiennych i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
Kryterium informacyjne nie jest jednak miarą absolutną, tzn. jeśli wszystkie porównywane modele źle opisują rzeczywistość w kryterium informacyjnym nie ma sensu szukać ostrzeżenia.
). W obu przypadkach element ten rośnie wraz ze wzrostem liczby zmiennych i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
Kryterium informacyjne nie jest jednak miarą absolutną, tzn. jeśli wszystkie porównywane modele źle opisują rzeczywistość w kryterium informacyjnym nie ma sensu szukać ostrzeżenia.
Kryterium informacyjne Akaikego (ang. Akaike information criterion)
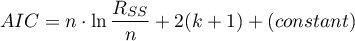
gdzie, stałą można pominąć, ponieważ jest taka sama w każdym z porównywanych modeli.
Jest to kryterium asymptotyczne - odpowiednie dla dużych prób tzn. gdy 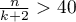 . Przy małych próbach ma tendencję do preferowania modeli z dużą liczbą zmiennych.
. Przy małych próbach ma tendencję do preferowania modeli z dużą liczbą zmiennych.
Przykład interpretacji porównania wielkości AIC
Załóżmy, że wyznaczyliśmy AIC dla trzech modeli AIC1=100, AIC2=101.4, AIC3=110. Wówczas można wyznaczyć względną wiarygodność dla modelu. Wiarygodność ta jest względna, gdyż wyznaczana jest względem innego modelu, najczęściej tego o najmniejszej wartości AIC. Wyznaczamy ją wg wzoru: exp((AICmin− AICi)/2). Porównując model 2 do modelu pierwszego powiemy, że prawdopodobieństwo, iż zminimalizuje on utratę informacji stanowi około połowę prawdopodobieństwa, że zrobi to model 1 (a dokładnie exp((100− 101.4)/2) = 0.497). Porównując model 3 do modelu pierwszego powiemy, że prawdopodobieństwo, iż zminimalizuje on utratę informacji stanowi niewielką część prawdopodobieństwa, że zrobi to model 1 (a dokładnie exp((100- 110)/2) = 0.007).
Poprawione kryterium informacyjne Akaikego
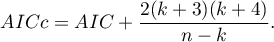
Poprawka kryterium Akaikego dotyczy wielkości próby, przez co jest to miara rekomendowana również dla prób o małych licznościach.
Bayesowskie kryterium informacyjne Schwartza (ang. Bayes Information Criterion lub Schwarz criterion)
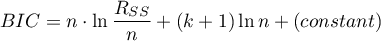
gdzie, stałą można pominąć, ponieważ jest taka sama w każdym z porównywanych modeli.
Podobnie jak poprawione kryterium Akaikego BIC uwzględnia wielkość próby.
- Analiza błędów dla prognoz ex post:
MAE (średni błąd bezwzględny) ang. mean absolute error – trafność prognozy określona przez MAE informuje o ile średnio uzyskiwane realizacje zmiennej zależnej będę się odchylać (co do wartości bezwzględnej) od prognoz.
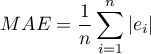
MPE (średni błąd procentowy) ang. mean percentage error – informuje, jaki średni procent realizacji zmiennej zależnej stanowią błędy prognozy.
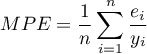
MAPE (średni bezwzględny błąd procentowy) ang. mean absolute percentage error – informuje o średniej wielkości błędów prognoz wyrażonych w procentach rzeczywistych wartości zmiennej zależnej. MAPE pozwala porównać dokładność prognoz uzyskanych na bazie różnych modeli.
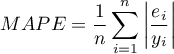
- Istotność statystyczna wszystkich zmiennych w modelu
Podstawowym narzędziem szacującym istotność wszystkich zmiennych w modelu jest test analizy wariancji (test F). Test ten weryfikuje jednocześnie 3 równoważne hipotezy:


Statystyka testowa ma postać:
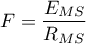
gdzie:
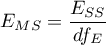 - średnia kwadratów wyjaśniona przez model,
- średnia kwadratów wyjaśniona przez model,
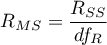 - resztowa średnia kwadratów,
- resztowa średnia kwadratów,
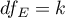 ,
, 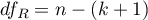 - odpowiednie stopnie swobody.
- odpowiednie stopnie swobody.
Statystyka ta podlega rozkładowi F Snedecora z 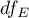 i
i 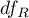 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Przykład c.d. (plik wydawca.pqs)
pl/statpqpl/wielowympl/wielorpl/weryfpl.txt · ostatnio zmienione: 2024/12/06 09:10 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

