Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:statpqpl:wielowympl:wielorpl:weryfpl
Model verification
- Statistical significance of particular variables in the model.
On the basis of the coefficient and its error of estimation we can infer if the independent variable for which the coefficient was estimated has a significant effect on the dependent variable. For that purpose we use t-test.
Hypotheses:
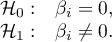
Let us estimate the test statistics according to the formula below:
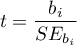
The test statistics has t-Student distribution with 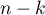 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

- The quality of the constructed model of multiple linear regression can be evaluated with the help of several measures.
- The standard error of estimation – it is the measure of model adequacy:
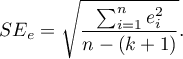
The measure is based on model residuals 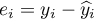 , that is on the discrepancy between the actual values of the dependent variable
, that is on the discrepancy between the actual values of the dependent variable 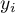 in the sample and the values of the independent variable
in the sample and the values of the independent variable 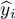 estimated on the basis of the constructed model. It would be best if the difference were as close to zero as possible for all studied properties of the sample. Therefore, for the model to be well-fitting, the standard error of estimation (
estimated on the basis of the constructed model. It would be best if the difference were as close to zero as possible for all studied properties of the sample. Therefore, for the model to be well-fitting, the standard error of estimation (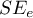 ), expressed as
), expressed as 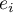 variance, should be the smallest possible.
variance, should be the smallest possible.
- Multiple correlation coefficient
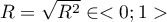 – defines the strength of the effect of the set of variables
– defines the strength of the effect of the set of variables  on the dependent variable
on the dependent variable  .
. - Multiple determination coefficient
 – it is the measure of model adequacy.
– it is the measure of model adequacy.
The value of that coefficient falls within the range of 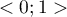 , where 1 means excellent model adequacy, 0 – a complete lack of adequacy. The estimation is made using the following formula:
, where 1 means excellent model adequacy, 0 – a complete lack of adequacy. The estimation is made using the following formula:
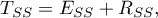
where:
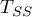 – total sum of squares,
– total sum of squares,
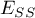 – the sum of squares explained by the model,
– the sum of squares explained by the model,
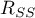 – residual sum of squares.
– residual sum of squares.
The coefficient of determination is estimated from the formula:
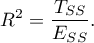
It expresses the percentage of the variability of the dependent variable explained by the model.
As the value of the coefficient 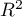 depends on model adequacy but is also influenced by the number of variables in the model and by the sample size, there are situations in which it can be encumbered with a certain error. That is why a corrected value of that parameter is estimated:
depends on model adequacy but is also influenced by the number of variables in the model and by the sample size, there are situations in which it can be encumbered with a certain error. That is why a corrected value of that parameter is estimated:
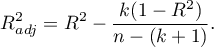
- Information criteria are based on the entropy of information carried by the model (model uncertainty) i.e. they estimate the information lost when a given model is used to describe the phenomenon under study. Therefore, we should choose the model with the minimum value of a given information criterion.
The 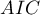 ,
, 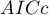 and
and 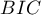 is a kind of trade-off between goodness of fit and complexity. The second element of the sum in the information criteria formulas (the so-called loss or penalty function) measures the simplicity of the model. It depends on the number of variables in the model (
is a kind of trade-off between goodness of fit and complexity. The second element of the sum in the information criteria formulas (the so-called loss or penalty function) measures the simplicity of the model. It depends on the number of variables in the model ( ) and the sample size (
) and the sample size ( ). In both cases, this element increases as the number of variables increases, and this increase is faster the smaller the number of observations.The information criterion, however, is not an absolute measure, i.e., if all the models being compared misdescribe reality in the information criterion there is no point in looking for a warning.
). In both cases, this element increases as the number of variables increases, and this increase is faster the smaller the number of observations.The information criterion, however, is not an absolute measure, i.e., if all the models being compared misdescribe reality in the information criterion there is no point in looking for a warning.
Akaike information criterion
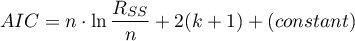
where, the constant can be omitted because it is the same in each of the compared models.
This is an asymptotic criterion - suitable for large samples i.e. when 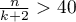 . For small samples, it tends to favor models with a large number of variables.
. For small samples, it tends to favor models with a large number of variables.
Example of interpretation of AIC size comparison
Suppose we determined the AIC for three models 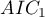 =100,
=100, 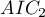 =101.4,
=101.4, 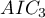 =110. Then the relative reliability for the model can be determined. This reliability is relative because it is determined relative to another model, usually the one with the smallest AIC value. We determine it according to the formula:
=110. Then the relative reliability for the model can be determined. This reliability is relative because it is determined relative to another model, usually the one with the smallest AIC value. We determine it according to the formula: 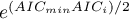 . Comparing model 2 to model 1, we will say that the probability that it will minimize the loss of information is about half of the probability that model 1 will do so (specifically exp((100− 101.4)/2) = 0.497). Comparing model 3 to model one, we will say that the probability that it will minimize information loss is a small fraction of the probability that model 1 will do so (specifically exp((100- 110)/2) = 0.007).
. Comparing model 2 to model 1, we will say that the probability that it will minimize the loss of information is about half of the probability that model 1 will do so (specifically exp((100− 101.4)/2) = 0.497). Comparing model 3 to model one, we will say that the probability that it will minimize information loss is a small fraction of the probability that model 1 will do so (specifically exp((100- 110)/2) = 0.007).
Akaike coreccted information criterion
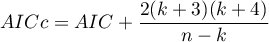
Correction of Akaike's criterion relates to sample size, which makes this measure recommended also for small sample sizes.
Bayes Information Criterion (or Schwarz criterion)
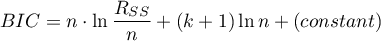
where, the constant can be omitted because it is the same in each of the compared models.
Like Akaike's revised criterion, the BIC takes into account the sample size.
- Error analysis for ex post forecasts:
MAE (mean absolute error) -– forecast accuracy specified by MAE informs how much on average the realised values of the dependent variable will deviate (in absolute value) from the forecasts.
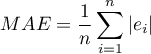
MPE (mean percentage error) -– informs what average percentage of the realization of the dependent variable are forecast errors.
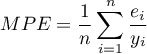
MAPE (mean absolute percentage error) -– informs about the average size of forecast errors expressed as a percentage of the actual values of the dependent variable. MAPE allows you to compare the accuracy of forecasts obtained from different models.
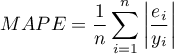
- Statistical significance of all variables in the model
The basic tool for the evaluation of the significance of all variables in the model is the analysis of variance test (the F-test). The test simultaneously verifies 3 equivalent hypotheses:


The test statistics has the form presented below:
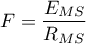
where:
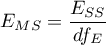 – the mean square explained by the model,
– the mean square explained by the model,
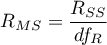 – residual mean square,
– residual mean square,
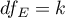 ,
, 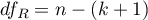 – appropriate degrees of freedom.
– appropriate degrees of freedom.
That statistics is subject to F-Snedecor distribution with 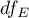 and
and 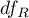 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:

EXAMPLE (publisher.pqs file)
en/statpqpl/wielowympl/wielorpl/weryfpl.txt · ostatnio zmienione: 2024/12/06 09:17 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

