Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Baza Wiedzy » statpqpl » Analizy opisowe » Statystyka opisowa
Pasek boczny
pl:statpqpl:aopisowapl:statopispl
Spis treści
Statystyka opisowa
Celem stosowania metod statystyki opisowej jest podsumowanie zbioru danych poprzez pewne charakterystyki np. poprzez wartość średniej, mediany czy odchylenia standardowego, oraz wyciągnięcie pewnych podstawowych wniosków i uogólnień na temat zbioru.
Aby wyznaczyć statystyki opisowe dla danych zgromadzonych w arkuszu należy wyświetlić okno Statystyki opisowe poprzez wybranie menu Statystyka→Statystyki opisowe.
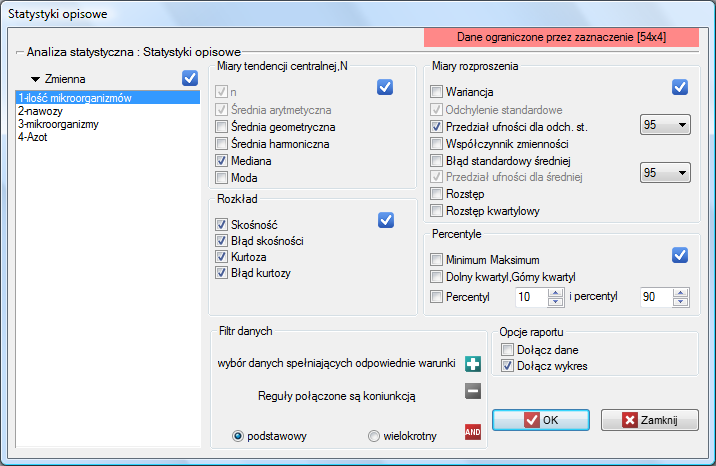
W oknie tym wybieramy zmienną do analizy oraz opcje analizy i zaznaczamy interesujące nas miary statystyk opisowych. Przy czym zaznaczać można pojedyncze statystyki lub grupy statystyk wybierając przycisk  . Dokonany wybór potwierdzamy przyciskiem
. Dokonany wybór potwierdzamy przyciskiem OK. Wynik dokonanej analizy znajdzie się w raporcie dołączonym do arkusza danych, dla których analiza została wykonana.
Dodatkowo, jeśli chcemy by dane zostały zobrazowane za pomocą wykresu ramka-wąsy, wówczas w oknie Statystyk opisowych zaznaczamy opcję Dołącz wykres.
Miary położenia
Miary tendencji centralnej
Miary tendencji centralnej są to tzw. miary przeciętne charakteryzujące średni lub typowy poziom wartości cechy.
Średnia arytmetyczna (ang. arithmetic mean) wyraża się wzorem:
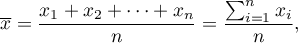
gdzie  to kolejne wartości zmiennej a
to kolejne wartości zmiennej a  - liczność próby.
- liczność próby.
Średnia arytmetyczna jest stosowana dla skali interwałowej. Dla próby przyjmuje się ją oznaczać przez  a dla populacji przez
a dla populacji przez  .
.
Średnia przycięta (Trimmed mean)- wyznaczana jest jako średnia arytmetyczna obliczona po usunięciu z próbki zadanego procentu najmniejszych i największych pomiarów np. gdy obcinamy 5% pomiarów, to oznacza, że obcinamy 2.5% największych i 2.5% najmniejszych wartości. Przy czym, gdy uzyskana na podstawie przeliczań liczba pomiarów przeznaczonych do usunięcia nie będzie liczbą całkowitą, wówczas jest ona zaokrąglana w dół do najbliższej całkowitej.
Średnia Winsora (Winsor mean) - wyznaczana jest jako średnia arytmetyczna obliczona po zastąpieniu odpowiedniego odsetka skrajnych pomiarów wartością najmniejszą i największą jaka pozostała zmniejszonym zbiorze wartości. Jeśli zdecydujemy się na obliczanie średniej Winsora przycinając np. 5% pomiarów, to wówczas te odrzucone 5% zostanie zastąpione wartością najmniejszą i największą wyznaczoną z pozostałych 95% pomiarów. Podobnie jak dla średniej przycinanej, gdy na podstawie przeliczenia procentu wartości przeznaczonych do zamiany na liczbę pomiarów przeznaczonych do zamiany nie uzyskamy liczby całkowitej, wówczas zaokrąglamy w dół do najbliższej całkowitej.
Średnia geometryczna (ang. geometric mean) wyraża się wzorem:
![LaTeX \begin{displaymath}
\overline{x}_G=\sqrt[n]{x_1x_2...x_n}=\sqrt[n]{\prod_{i=1}^n x_i}.
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img011017a5d163d0e6305611f865ade072.png) Średnia ta jest stosowana dla skali interwałowej, gdy zmienna ma rozkład logarytmiczno-normalny (logarytm zmiennej ma rozkład normalny).
Średnia ta jest stosowana dla skali interwałowej, gdy zmienna ma rozkład logarytmiczno-normalny (logarytm zmiennej ma rozkład normalny).
Średnia harmoniczna (ang. harmonic mean) wyraża się wzorem:
 Średnia ta jest stosowana dla skali interwałowej.
Średnia ta jest stosowana dla skali interwałowej.
W uporządkowanym zbiorze danych mediana jest wartością dzielącą ten zbiór na dwie równe części. Połowa wszystkich obserwacji znajduje się poniżej, a połowa powyżej mediany.
![LaTeX \begin{pspicture}(0,0)(10,10.6)
\pscoil[coilaspect=0, coilarm=.1cm, linewidth=0.5pt, coilwidth=.5cm, coilheight=1]{-}(0,4)
\rput(0,4.2){min}
\rput(0,-.2){max}
\psline(-0.35,2)(.35,2)
\rput(1.2,2){mediana}
\rput(-0.6,2.8){50$\%$}
\rput(-0.6,1.2){50$\%$}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img826223981ace04d4f37d432b7063428a.png)
Mediana może być stosowana w skali interwałowej oraz porządkowej.
Moda  jest to wartość, która występuje najczęściej wśród uzyskanych pomiarów. Moda może być stosowana w każdej skali pomiarowej.
jest to wartość, która występuje najczęściej wśród uzyskanych pomiarów. Moda może być stosowana w każdej skali pomiarowej.
2022/01/23 17:58
· admin
Inne miary położenia
kwartyle (ang. quartiles), decyle (ang. deciles), centyle (ang. centiles)
![LaTeX \begin{pspicture}(0,-.2)(4,4.4)
\pscoil[coilaspect=0, coilarm=.1cm, linewidth=0.5pt, coilwidth=.5cm, coilheight=1]{-}(0,4)
\rput(0,4.2){max}
\rput(0,-.2){min}
\psline(-0.35,3)(.35,3)
\psline(-0.35,2)(.35,2)
\psline(-0.35,1)(.35,1)
\rput(2.9,3){$C_{75}$ = kwartyl górny = $Q_3$}
\rput(2.4,2){$C_{50}$ = mediana = $Q_2$}
\rput(2.9,1){$C_{25}$ = kwartyl dolny = $Q_1$}
\rput(1,3.5){25$\%$}
\rput(1,2.5){25$\%$}
\rput(1,1.5){25$\%$}
\rput(1,.5){25$\%$}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img95cc67a481e2d6314660a8aa6c567235.png)
Kwartyle (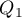 ,
, 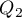 ,
, 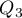 ) dzielą uporządkowany szereg na 4 równe części, decyle (
) dzielą uporządkowany szereg na 4 równe części, decyle (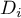 ,
, 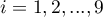 ) na 10 równych części a centyle (percentyle:
) na 10 równych części a centyle (percentyle: 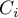 ,
, 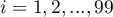 ) na 100 równych części. Drugi kwartyl, piąty decyl i pięćdziesiąty centyl są równe medianie. Miary te mogą być stosowane w skali interwałowej oraz porządkowej.
) na 100 równych części. Drugi kwartyl, piąty decyl i pięćdziesiąty centyl są równe medianie. Miary te mogą być stosowane w skali interwałowej oraz porządkowej.
2022/01/23 17:59
· admin
2022/01/23 17:58
· admin
Miary rozproszenia
Znajomość miar tendencji centralnej nie wystarcza do scharakteryzowania struktury zbiorowości statystycznej. Badana grupa może charakteryzować się różnym stopniem zmienności w zakresie badanej cechy. Potrzebne są zatem formuły pozwalające wyznaczyć wartości, które charakteryzują rozrzut danych.
Miary rozproszenia są liczone tylko dla skali interwałowej, ponieważ bazują one na odległościach między punktami.
Rozstęp (ang. range) wyraża się wzorem:
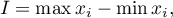
gdzie  to wartości badanej zmiennej
to wartości badanej zmiennej
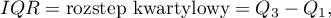
gdzie 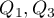 to dolny i górny kwartyl.
to dolny i górny kwartyl.
Rozstępy dla skali percentylowej (decylowej, centylowej). Rozstępy miedzy percentylami to jedna z miar rozproszenia i określa procent wszystkich obserwacji, których wartość znajduje się pomiędzy wybranymi percentylami.
Wariancja (ang. variance) - mierzy stopień rozproszenia pomiarów wokół średniej arytmetycznej
- wariancja z próby:
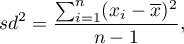
gdzie  to kolejne wartości zmiennej a
to kolejne wartości zmiennej a 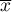 to średnia arytmetyczna tych wartości,
to średnia arytmetyczna tych wartości,  - liczność próby.
- liczność próby.
- wariancja z populacji:
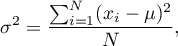
gdzie  to kolejne wartości zmiennej a
to kolejne wartości zmiennej a 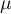 to średnia arytmetyczna tych wartości,
to średnia arytmetyczna tych wartości, 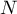 - liczność populacji.
- liczność populacji.
Wariancja jest zawsze dodatnia, ale nie jest wyrażona w tych samych jednostkach co wyniki pomiarów.
Odchylenie standardowe (ang. standard deviation)  mierzy stopień rozproszenia pomiarów wokół średniej arytmetycznej.
mierzy stopień rozproszenia pomiarów wokół średniej arytmetycznej.
- odchylenie standardowe z próby:
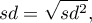
- odchylenie standardowe z populacji:
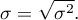
Im wyższa wartość odchylenia standardowego lub wariancji, tym bardziej zróżnicowana grupa pod względem badanej cechy.
Uwaga! Odchylenie standardowe z próby jest pewnym przybliżeniem (estymatorem) odchylenia standardowego z populacji. Populacyjna wartość odchylenia standardowego mieści się w pewnym przedziale zawierającym odchylenie standardowe z próby. Przedział ten nazywany jest przedziałem ufności (confidence interval) dla odchylenia standardowego.
Współczynnik zmienności (ang. coefficient of variation)
Współczynnik zmienności podobnie jak odchylenie standardowe pozwala na ocenę stopnia jednorodności badanej zbiorowości. Wyraża się wzorem:
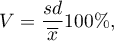
gdzie 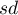 to odchylenie standardowe,
to odchylenie standardowe, 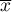 to średnia arytmetyczna.
to średnia arytmetyczna.
Jest to wielkość niemianowana. Pozwala on na ocenę zróżnicowania kilku zbiorowości pod względem tej samej cechy oraz tej samej zbiorowości pod względem kilku różnych cech (wyrażonych w różnych jednostkach). Przyjmuje się, że jeżeli współczynnik 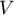 nie przekracza 10\%, to cechy wykazują zróżnicowanie statystycznie nieistotne.
nie przekracza 10\%, to cechy wykazują zróżnicowanie statystycznie nieistotne.
Błędy standardowe (ang. standard errors) - nie są miarami rozproszenia wyników pomiarowych, lecz określają stopień dokładności z jaką możemy określić wartości parametrów populacji na podstawie wyznaczenia ich estymatorów dla próby.
Błąd średniej arytmetycznej (ang. standard error of the mean) wyraża się następującym wzorem:
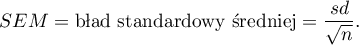
Uwaga! Na podstawie błędu standardowego estymatora z próby można określić przedział ufności dla parametru populacji.
2022/01/23 18:00
· admin
Inne atrybuty rozkładu
Skośność inaczej współczynnik asymetrii (ang. skewness)
Jest to miara, która mówi o tym jak bardzo rozkład danych różni się od rozkładu symetrycznego. Im wartość współczynnika asymetrii jest bliższa zeru, tym bardziej symetrycznie wokół średniej rozkładają się dane. Zwykle wartość tego współczynnika zawiera się w przedziale [-1, 1], chociaż może w przypadku szczególnie dużej asymetrii znaleźć się poza tym przedziałem. Wartości dodatnie świadczą o występowaniu skośności prawostronnej (o dłuższym prawym „ogonie”) wartości ujemne zaś o skośności lewostronnej (o dłuższym lewym „ogonie”). Skośność wyraża się wzorem:
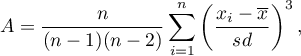
gdzie:
 – kolejne wartości zmiennej,
– kolejne wartości zmiennej,
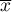 ,
, 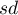 – odpowiednio średnia arytmetyczna i odchylenie standardowe
– odpowiednio średnia arytmetyczna i odchylenie standardowe  ,
,
 – liczność próby.
– liczność próby.
![LaTeX \begin{tabular}{cc}
\begin{pspicture}(0,-.7)(7,3.6)
\rput(2.5,3.3){skośność prawostronna}
\rput(2.8,2.8){$A>0$}
\psline{->}(0,0)(0,3)
\psline{->}(0,0)(6.3,0)
\psbezier{-}(.2,.2)(.5,.2)(.7,2.3)(1.3,2.5)
\psbezier{-}(1.3,2.5)(2,2.5)(3,.2)(5.3,.2)
\psline[linestyle=dotted]{-}(2.2,0)(2.2,1.7)
\rput(2.55,-.3){Med.}
\psline[linestyle=dotted]{-}(1.3,0)(1.3,2.5)
\rput(1.3,-.3){Moda}
\psline[linestyle=dotted]{-}(3.4,0)(3.4,.7)
\rput(3.5,-.3){$\overline{X}$}
\rput{90}(-.4,2.7){częstość}
\rput(6.1,-.3){x}
\end{pspicture}
&
\begin{pspicture}(0,-.7)(7,3.6)
\rput(2.5,3.3){skośność lewostronna}
\rput(2.2,2.8){$A<0$}
\psline{->}(0,0)(0,3)
\psline{->}(0,0)(6.3,0)
\psbezier{-}(.2,.2)(2.1,.2)(2.8,2.5)(3.7,2.5)
\psbezier{-}(3.7,2.5)(4.2,2.5)(4.8,.2)(5.5,.2)
\psline[linestyle=dotted]{-}(2.85,0)(2.85,1.75)
\rput(2.7,-.3){Med.}
\psline[linestyle=dotted]{-}(3.7,0)(3.7,2.5)
\rput(3.9,-.3){Moda}
\psline[linestyle=dotted]{-}(1.7,0)(1.7,.7)
\rput(1.7,-.3){$\overline{X}$}
\rput{90}(-.4,2.7){częstość}
\rput(6.1,-.3){x}
\end{pspicture}
\end{tabular}](/lib/exe/fetch.php?media=wiki:latex:/img0e1a8fde93ad1f126fa614ca317cb07a.png)
Kurtoza inaczej współczynnik koncentracji (ang. kurtosis)
Jest to miara, która mówi o tym jak bardzo rozrzut danych wokół średniej jest zbliżony do rozrzutu tych danych w rozkładzie normalnym. Im wartość kurtozy jest większa od zera, tym badany rozkład jest bardziej smukły niż rozkład normalny a im wartość kurtozy jest mniejsza od zera, tym badany rozkład jest bardziej spłaszczony niż rozkład normalny. Kurtoza wyraża się wzorem:
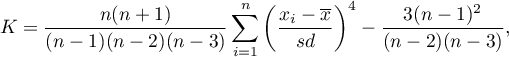
gdzie:
 – kolejne wartości zmiennej,
– kolejne wartości zmiennej,
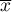 ,
, 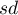 – odpowiednio średnia arytmetyczna i odchylenie standardowe
– odpowiednio średnia arytmetyczna i odchylenie standardowe  ,
,
 – liczność próby.
– liczność próby.
![LaTeX \begin{pspicture}(0,-.8)(6.5,3.4)
\rput(4.0,.7){$K_1<0$}
\rput(4.5,2.5){$K_2>0$}
\psline{->}(0,0)(0,3)
\psline{->}(0,0)(7,0)
\psbezier[linestyle=dashed]{-}(.2,.2)(2.2,.8)(2.3,1.4)(3.2,1.5)
\psbezier[linestyle=dashed]{-}(3.2,1.5)(4.1,1.4)(4.2,.8)(6.2,.2)
\psbezier{-}(.4,.2)(2.4,.6)(2.5,3.0)(3.2,3.1)
\psbezier{-}(3.2,3.1)(3.9,3.0)(4.0,.6)(6.0,.2)
\psline[linestyle=dotted]{-}(3.2,0)(3.2,3.1)
\rput(3.2,-.3){$\overline{X}$}
\rput{90}(-.4,2.7){częstość}
\rput(6.8,-.3){x}
\end{pspicture}](/lib/exe/fetch.php?media=wiki:latex:/img1db9eb4b65eaf100bd5055c2b3a9f66c.png)
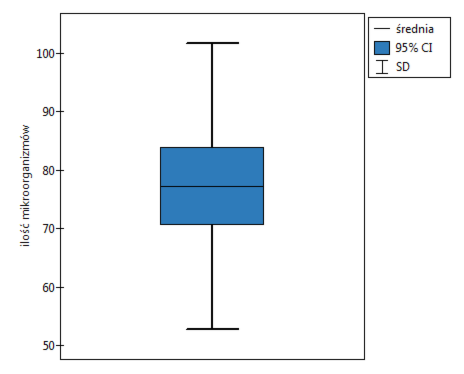
Przykład (plik nawozy.pqs)
W doświadczeniu dotyczącym nawożenia gleby różnymi rodzajami preparatów mikrobiologicznych i nawozów wyliczono ilość mikroorganizmów występujących w 1 gramie suchej masy gleby. Chcemy wyznaczyć statystyki opisowe ilości promieniowców dla próbki nawożonej azotem i zobrazować uzyskane wyniki za pomocą wykresu ramka-wąsy. Zaznaczamy w arkuszu danych tylko 54 pierwsze wiersze, które odpowiadają założeniom analizy (są to promieniowce nawożone azotem) i uruchamiamy okno Statystyki opisowe poprzez menu Statystyka→Statystyki opisowe.
W oknie opcji testu statystyk opisowych wybieramy zmienną do analizy: Ilość mikroorganizmów, a następnie procedury jakie chcemy wykonać (np. średnią arytmetyczną wraz z przedziałem ufności, medianę, odchylenie standardowe wraz z przedziałem ufności oraz informacje o skośności i kurtozie rozkładu wraz z błędami). Na górze okna powinien być widoczny komunikat:
Dane ograniczone przez zaznaczenie
By w raporcie znalazł się również wykres, zaznaczamy opcję Dołącz wykres i wybieramy interesujący nas rodzaj wykresu ramka-wąsy. Potwierdzamy wybór przyciskiem OK i uzyskujemy wynik w postaci raportu:

2022/01/23 18:00
· admin
pl/statpqpl/aopisowapl/statopispl.txt · ostatnio zmienione: 2022/01/23 18:15 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

