Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:wielowympl:logistpl:wykresy
Wykresy w regresji logistycznej
- Iloraz szans i przedział ufności - to wykres przedstawiający OR wraz z 95% przedziałem ufności dla wyniku każdej zmiennej zwróconej w zbudowanym modelu. Dla zmiennych kategorialnych, linia na poziomie 1 wskazuje wartość ilorazu szans dla kategorii referencyjnej.
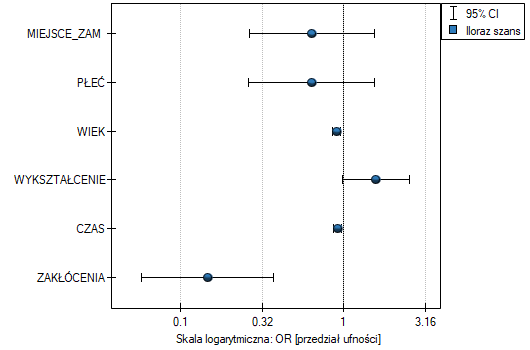
- Wartości obserwowane / Prawdopodobieństwo oczekiwane - to wykres przedstawiający wyniki przewidywanego dla każdej osoby prawdopodobieństwa wystąpienia zdarzenia (oś X) oraz wartości prawdziwej, czyli wystąpienia zdarzenia (wartość 1 na osi Y) lub braku zdarzenia (wartość 0 na osi Y). Jeśli model bardzo dobrze prognozuje, to przy lewej stronie wykresu punkty będą się kumulowały w dolnej części, a przy prawej stronie wykresu w górnej części.
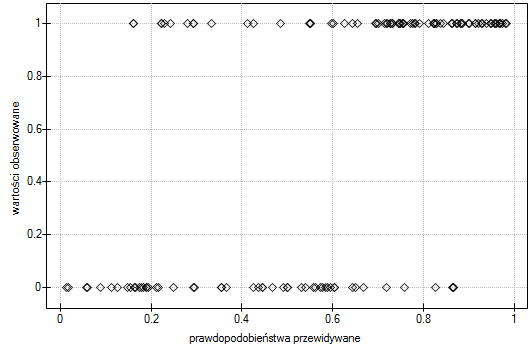
- Krzywa ROC - to wykres zbudowany w oparciu o wartość zmiennej zależnej oraz przewidywane prawdopodobieństwo wystąpienia zdarzenia.
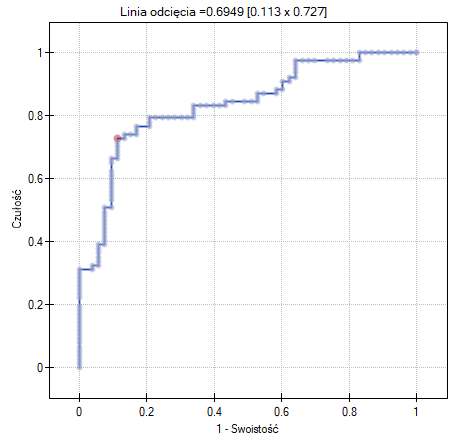
- Wykres reszt Pearsona - to wykres pozwalający ocenić czy występują odstające dane. Reszty to różnice wartości obserwowanej i przewidywanego przez model prawdopodobieństwa. Wykresy surowych reszt z regresji logistycznej trudno interpretować, dlatego ujednolica się je wyznaczając reszty Pearsona. Reszta Pearsona to surowa reszta podzielona przez pierwiastek kwadratowy z funkcji wariancji. Znak (dodatni lub ujemny) wskazuje, czy obserwowana wartość jest wyższa, czy niższa niż wartość dopasowana do modelu, a wielkość wskazuje stopień odchylenia. Reszty Persona mniejsze lub większe niż 3 sugerują, zbyt duże odchylenie danego obiektu.
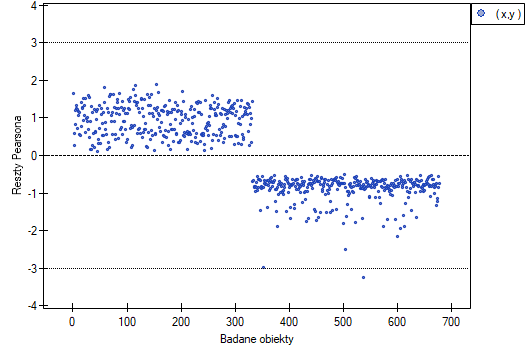
- Jednostkowe zmiany ilorazu szans - to wykres przedstawiający serie ilorazów szans wraz z przedziałem ufności, wyznaczane dla każdego z możliwych punktów odcięcia zmiennej umieszczonej na osi X. Umożliwia on użytkownikowi wybór jednego, dobrego punktu odcięcia i następnie zbudowania na tej podstawie nowej dwuwartościowej zmiennej, przy której zostanie osiągnięty odpowiednio wysoki lub niski iloraz szans. Wykres dedykowany jest dla oceny zmiennych ciągłych w analizie jednoczynnikowej, tzn. gdy wybrana jest tylko jedna zmienna niezależna.
- Profile ilorazu szans - to wykres przedstawiający serie ilorazów szans wraz z przedziałem ufności, wyznaczane dla wskazanej wielkości okna tzn. porównujące częstości wewnątrz okna z częstościami umieszczonymi na zewnątrz okna. Umożliwia to użytkownikowi wybór kilku kategorii na jakie chce podzielić badaną zmienną i przyjęcie najkorzystniejszej kategorii referencyjnej. Najlepiej sprawdza się, gdy poszukujemy funkcji U-kształtnej tzn. o wysokim ryzyku przy niskich i przy wysokich wartościach badanej zmiennej, a o niskim przy wartościach przeciętnych. Nie ma jednej dobrej dla każdej analizy wielkości okna, wielkość tę należy ustalać indywidualnie dla każdej zmiennej. Wielkość okna wskazuje liczbę niepowtarzalnych wartości zmiennej X znajdujących się w oknie. Im szersze okno, tym większe uogólnienie wyników i gładsza funkcja ilorazu szans. Im węższe okno, tym bardziej szczegółowe wyniki, przez co bardziej rozchwiany iloraz szans. Do wykresu dodana jest krzywa ukazująca wygładzoną (metodą Lowess) wartość ilorazu szans. Ustawiając bliski 0 współczynnik wygładzania uzyskamy krzywą przylegającą ściśle do wyznaczonego ilorazu szans, natomiast ustawiając współczynnik wygładzania bliżej 1 dostaniemy większe uogólnienie ilorazu szans, a więc bardziej gładką i mniej przyległą do ilorazu szans krzywą. Wykres dedykowany jest dla oceny zmiennych ciągłych w analizie jednoczynnikowej, tzn. gdy wybrana jest tylko jedna zmienna niezależna.
Przykład (plik Profile OR.pqs)
Badamy ryzyko występowania choroby A i choroby B w zależności od BMI pacjenta. Ponieważ BMI jest zmienną ciągłą, to jej umieszczenie w modelu skutkuje wyznaczeniem jednostkowego ilorazu szans wyznaczającego liniowy trend wzrostu lub spadku ryzyka. Nie wiemy czy model liniowy będzie dobrym modelem dla analizy tego ryzyka, dlatego przed budowaniem wielowymiarowych modeli regresji logistycznej zbudujemy kilka modeli jednowymiarowych prezentujących tę zmienną na wykresach, by móc ocenić kształt badanej zależności i na tej podstawie zdecydować o sposobie w jaki powinniśmy przygotować zmienną do analizy. Do tego celu posłużą wykresy jednostkowych zmiany ilorazu szans i profili ilorazu szans, przy czym dla profili wybierzemy okno o wielkości 100, ponieważ prawie każdy pacjent ma inne BMI, więc około 100 pacjentów znajdzie się w każdym oknie.
- Choroba A
Jednostkowe zmiany ilorazu szans pokazują, że gdy punkt odcięcia BMI wybierzemy gdzieś między 27 a 37, to uzyskamy istotny statystycznie i dodatni iloraz szans pokazujący, że osoby mające BMI powyżej tej wartości mają istotnie wyższe ryzyko choroby niż osoby poniżej tej wartości.
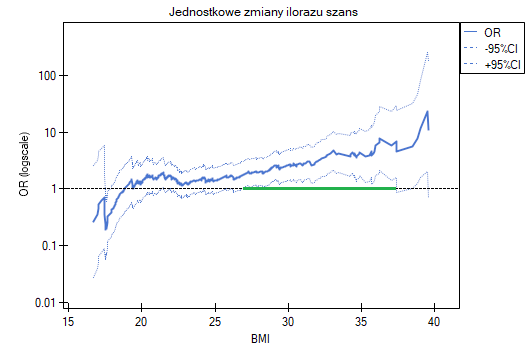
Profile ilorazu szans pokazują, że czerwona krzywa znajduje się wciąż blisko jedynki, nieco wyżej jest tylko końcówka krzywej, co wskazuje że może być trudno podzielić BMI na więcej niż 2 kategorie i wybrać dobrą kategorię referencyjną, tzn. taką, która da istotne ilorazy szans.
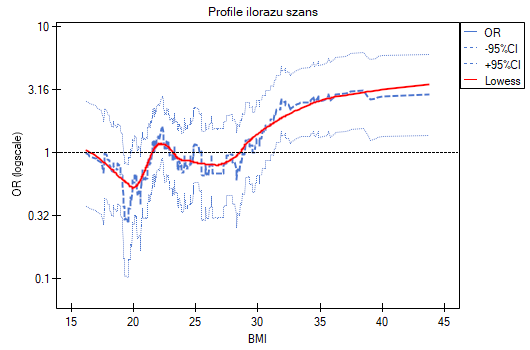
Podsumowując, można skorzystać z podziału BMI na dwie wartości (np. odnieść osoby z BMI powyżej 30 do tych z BMI poniżej tej granicy, wówczas OR[95%CI]=[1.41, 4.90], p=0.0024) lub pozostać przy jednostkowym ilorazie szans, wskazującym stały wzrost ryzyka choroby przy wzroście BMI o jednostkę (OR[95%CI]=1.07[1.02, 1.13], p=0.0052).
- Choroba B
Jednostkowe zmiany ilorazu szans pokazują, że gdy punkt odcięcia BMI wybierzemy gdzieś między 22 a 35, to uzyskamy istotny statystycznie i dodatni iloraz szans pokazujący, że osoby mające BMI powyżej tej wartości mają istotnie wyższe ryzyko choroby niż osoby poniżej tej wartości.
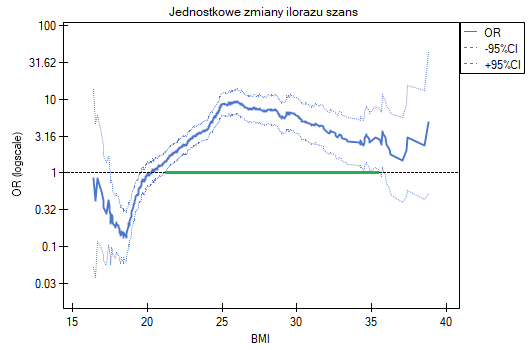
Profile ilorazu szans pokazują, że znacznie lepiej byłoby podzielić BMI na 2 lub 4 kategorie. Przy czym kategorią referencyjną powinna być kategoria obejmująca BMI gdzieś pomiędzy 19 a 25, ponieważ to ta kategoria znajduje się najniżej i jest mocno oddalona od wyników dla BMI znajdujących się na lewo i na prawo od tego przedziału. Widzimy wyraźny kształt przypominający literę U, co oznacza, że ryzyko choroby jest wysokie przy niskim i przy wysokim BMI.
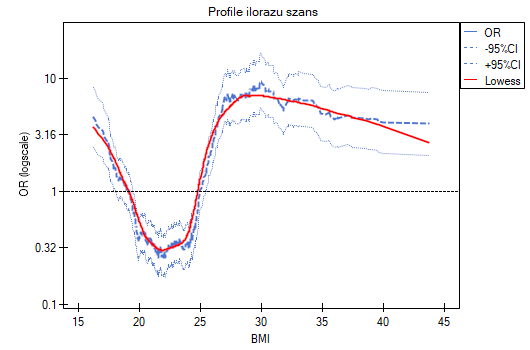
Podsumowując, mimo, że zależność dla jednostkowego ilorazu szans, czyli zależność liniowa jest istotna statystycznie, to nie warto budować takiego właśnie modelu. Znacznie lepiej podzielić BMI na kategorie. Podział pokazujący najlepiej kształt tej zależności, to podział wykorzystujący dwie lub trzy kategorie BMI, gdzie wartością odniesienia będzie przeciętne BMI. Wykorzystując standardowy podział BMI i ustanawiając kategorią odniesienia BMI w normie uzyskamy ponad 15 krotnie wyższe ryzyko dla osób z niedowagą (OR[95%CI]=15.14[6.93, 33.10]), ponad dziesięciokrotnie dla osób z nadwagą (OR[95%CI]=10.35[6.74, 15.90]) i ponad dwunastokrotnie dla osób z otyłością (OR[95%CI]=12.22[6.94, 21.49]).
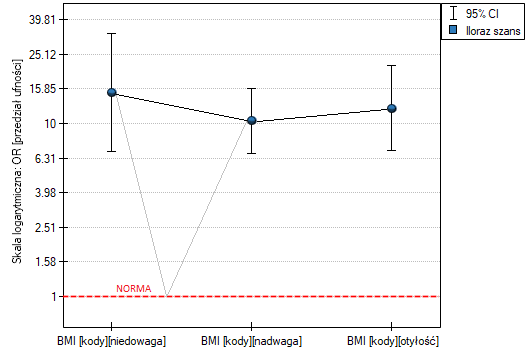
Na wykresie ilorazów szans norma BMI wskazana jest na poziomie 1, jako kategoria referencyjna. Dorysowaliśmy linie łączące uzyskane OR i również normę, tak by pokazać, że uzyskany kształt zależności jest tożsamy z wyznaczonym wcześniej poprzez profil ilorazu szans.
statpqpl/wielowympl/logistpl/wykresy.txt · ostatnio zmienione: 2021/02/23 20:27 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


