Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Modele wielowymiarowe » Regresja logistyczna » Weryfikacja modelu
Pasek boczny
statpqpl:wielowympl:logistpl:werpl
Weryfikacja modelu
Istotność statystyczna poszczególnych zmiennych w modelu (istotność ilorazu szans)
Na podstawie współczynnika oraz jego błędu szacunku możemy wnioskować czy zmienna niezależna, dla której ten współczynnik został oszacowany wywiera istotny wpływ na zmienną zależną. W tym celu posługujemy się testem Walda.
Hipotezy:
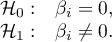 lub równoważnie:
lub równoważnie:
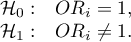
Statystykę testową testu Walda wyliczamy według wzoru:
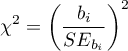 Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z  stopniem swobody .
stopniem swobody .
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Jakość zbudowanego modelu
Dobry model powinien spełniać dwa podstawowe warunki: powinien być dobrze dopasowany i możliwie jak najprostszy. Jakość modelu regresji logistycznej możemy ocenić kilkoma miarami, które opierają się na:
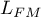 - maksimum funkcji wiarygodności modelu pełnego (z wszystkimi zmiennymi),
- maksimum funkcji wiarygodności modelu pełnego (z wszystkimi zmiennymi),
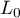 - maksimum funkcji wiarygodności modelu zawierającego jedynie wyraz wolny,
- maksimum funkcji wiarygodności modelu zawierającego jedynie wyraz wolny,
 - liczności próby.
- liczności próby.
- Kryteria informacyjne opierają się na entropii informacji niesionej przez model (niepewności modelu) tzn. szacują utraconą informację, gdy dany model jest używany do opisu badanego zjawiska. Powinniśmy zatem wybierać model o minimalnej wartości danego kryterium informacyjnego.
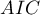 ,
, 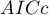 i
i 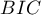 jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby zmiennych w modelu (
jest rodzajem kompromisu pomiędzy dobrocią dopasowania i złożonością. Drugi element sumy we wzorach na kryteria informacyjne (tzw. funkcja straty lub kary) mierzy prostotę modelu. Zależy on od liczby zmiennych w modelu ( ) i liczności próby (
) i liczności próby ( ). W obu przypadkach element ten rośnie wraz ze wzrostem liczby zmiennych i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
). W obu przypadkach element ten rośnie wraz ze wzrostem liczby zmiennych i wzrost ten jest tym szybszy im mniejsza jest liczba obserwacji.
Kryterium informacyjne nie jest jednak miarą absolutną, tzn. jeśli wszystkie porównywane modele źle opisują rzeczywistość w kryterium informacyjnym nie ma sensu szukać ostrzeżenia.
- Kryterium informacyjne Akaikego (ang. Akaike information criterion)
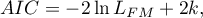
Jest to kryterium asymptotyczne - odpowiednie dla dużych prób.
- Poprawione kryterium informacyjne Akaikego
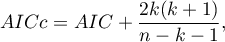
Poprawka kryterium Akaikego dotyczy wielkości próby, przez co jest to miara rekomendowana również dla prób o małych licznościach.
- Bayesowskie kryterium informacyjne Schwartza (ang. Bayes Information Criterion lub Schwarz criterion)
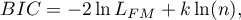
Podobnie jak poprawione kryterium Akaikego uwzględnia wielkość próby.
- Pseudo R
 - tzw. McFadden R
- tzw. McFadden R jest miarą dopasowania modelu (odpowiednikiem współczynnika determinacji wielorakiej
jest miarą dopasowania modelu (odpowiednikiem współczynnika determinacji wielorakiej  wyznaczanego dla liniowej regresji wielorakiej) .
wyznaczanego dla liniowej regresji wielorakiej) .
Wartość tego współczynnika mieści się w przedziale 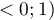 , gdzie wartości bliskie 1 oznaczają doskonałe dopasowanie modelu,
, gdzie wartości bliskie 1 oznaczają doskonałe dopasowanie modelu, 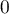 - zupełny bark dopasowania. Współczynnik
- zupełny bark dopasowania. Współczynnik 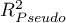 wyliczamy z wzoru:
wyliczamy z wzoru:
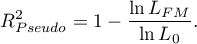
Ponieważ współczynnik 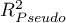 nie przyjmuje wartości 1 i jest wrażliwy na ilość zmiennych w modelu, wyznacza się jego poprawioną wartość:
nie przyjmuje wartości 1 i jest wrażliwy na ilość zmiennych w modelu, wyznacza się jego poprawioną wartość:
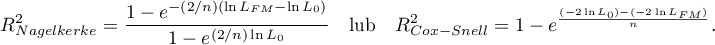
- Istotność statystyczna wszystkich zmiennych w modelu
Podstawowym narzędziem szacującym istotność wszystkich zmiennych w modelu jest test ilorazu wiarygodności. Test ten weryfikuje hipotezę:
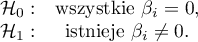
Statystyka testowa ma postać:
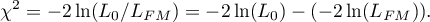
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z  stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

- Test Hosmera-Lemeshowa - Test ten, dla różnych podgrup danych, porównuje obserwowane liczności występowania wartości wyróżnionej
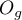 i przewidywane prawdopodobieństwo
i przewidywane prawdopodobieństwo 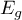 . Jeśli
. Jeśli 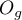 i
i 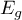 są wystarczająco bliskie, wówczas można założyć, że zbudowano dobrze dopasowany model.
są wystarczająco bliskie, wówczas można założyć, że zbudowano dobrze dopasowany model.
Do obliczeń najpierw obserwacje są dzielone na 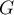 podgrup - zwykle na decyle (
podgrup - zwykle na decyle (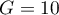 ).
).
Hipotezy:
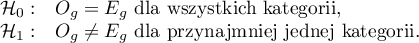
Statystyka testowa ma postać:
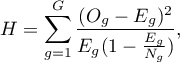 gdzie:
gdzie:
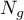 - liczba obserwacji w grupie
- liczba obserwacji w grupie 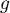 .
.
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 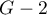 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

 AUC - pole pod krzywą ROC - Krzywa ROC, zbudowana w oparciu o wartość zmiennej zależnej oraz przewidywane prawdopodobieństwo zmiennej zależnej
AUC - pole pod krzywą ROC - Krzywa ROC, zbudowana w oparciu o wartość zmiennej zależnej oraz przewidywane prawdopodobieństwo zmiennej zależnej 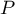 , pozwala na ocenę zdolności zbudowanego modelu regresji logistycznej do klasyfikacji przypadków do dwóch grup: (1) i (0). Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną modelu. Gdy krzywa ROC pokrywa się z przekątną
, pozwala na ocenę zdolności zbudowanego modelu regresji logistycznej do klasyfikacji przypadków do dwóch grup: (1) i (0). Powstała w ten sposób krzywa, a w szczególności pole pod nią, obrazuje jakość klasyfikacyjną modelu. Gdy krzywa ROC pokrywa się z przekątną  , to decyzja o przyporządkowaniu przypadku do wybranej klasy (1) lub (0) podejmowana na podstawie modelu jest tak samo dobra jak losowy podział badanych przypadków do tych grup. Jakość klasyfikacyjna modelu jest dobra, gdy krzywa znajduje się znacznie powyżej przekątnej
, to decyzja o przyporządkowaniu przypadku do wybranej klasy (1) lub (0) podejmowana na podstawie modelu jest tak samo dobra jak losowy podział badanych przypadków do tych grup. Jakość klasyfikacyjna modelu jest dobra, gdy krzywa znajduje się znacznie powyżej przekątnej  , czyli gdy pole pod krzywą ROC jest znacznie większe niż pole pod prostą
, czyli gdy pole pod krzywą ROC jest znacznie większe niż pole pod prostą  , zatem większe niż
, zatem większe niż 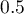
Hipotezy:
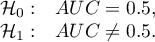
Statystyka testowa ma postać:
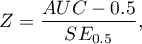 gdzie:
gdzie:
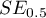 - błąd pola.
- błąd pola.
Statystyka  ma asymptotycznie (dla dużych liczności) rozkład normalny.
ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Dodatkowo, dla krzywej ROC podawana jest proponowana wartość punktu odcięcia prawdopodobieństwa przewidywanego, oraz tabela podająca wielkość czułości i swoistości dla każdego możliwego punktu odcięcia.
Uwaga! Więcej możliwości w wyliczeniu punktu odcięcia daje moduł **Krzywa ROC**. Analizę przeprowadzamy na podstawie wartości obserwowanych i prawdopodobieństwa przewidywanego, które uzyskujemy w analizie regresji logistycznej.
- Klasyfikacja
Na podstawie wybranego punktu odcięcia prawdopodobieństwa przewidywanego można sprawdzić jakość klasyfikacji. Punkt odcięcia, to domyślnie wartość 0.5. Użytkownik może zmienić tę wartość na dowolną wartość z przedziału 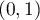 np. wartość sugerowaną przez krzywą ROC.
np. wartość sugerowaną przez krzywą ROC.
W wyniku uzyskamy tabelę klasyfikacji oraz procent poprawnie zaklasyfikowanych przypadków, procent poprawnie zaklasyfikowanych (0) - swoistość oraz procent poprawnie zaklasyfikowanych (1) - czułość.
statpqpl/wielowympl/logistpl/werpl.txt · ostatnio zmienione: 2021/01/07 22:45 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

