Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Modele wielowymiarowe » Regresja logistyczna » Iloraz Szans
Pasek boczny
statpqpl:wielowympl:logistpl:orpl
Iloraz Szans
Jednostkowy Iloraz Szans
Na podstawie współczynników, dla każdej zmiennej niezależnej w modelu, wylicza się łatwą w interpretacji miarę jaką jest jednostkowy Iloraz Szans:
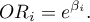
Otrzymany Iloraz Szans wyraża zmianę szansy na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna rośnie o 1 jednostkę. Wynik ten jest skorygowany o pozostałe zmienne niezależne znajdujące się w modelu w ten sposób, że zakłada iż pozostają one na stałym poziomie podczas, gdy badana zmienna niezależna rośnie o jednostkę.
Wartość OR interpretujemy następująco:
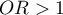 oznacza stymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile wzrasta szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.
oznacza stymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile wzrasta szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.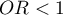 oznacza destymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile spada szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.
oznacza destymulujący wpływ badanej zmiennej niezależnej na uzyskanie wyróżnionej wartości (1), tj. mówi o ile spada szansa na wystąpienie wyróżnionej wartości (1), gdy zmienna niezależna wzrasta o jeden poziom.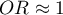 oznacza, że badana zmienna niezależna nie ma wpływu na uzyskanie wyróżnionej wartości (1).
oznacza, że badana zmienna niezależna nie ma wpływu na uzyskanie wyróżnionej wartości (1).
[Iloraz Szans - wzór ogólny]
Program PQStat wylicza jednostkowy Iloraz Szans. Jego modyfikacja, na podstawie ogólnego wzoru, umożliwia zmianę interpretacji uzyskanego wyniku.
Iloraz szans na wystąpienie stanu wyróżnionego w ogólnym przypadku jest wyliczany jako iloraz dwóch szans. Zatem dla zmiennej niezależnej  dla
dla  wyrażonego zależnością liniową wyliczamy:
wyrażonego zależnością liniową wyliczamy:
szansę dla kategorii pierwszej:
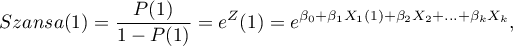
szansę dla kategorii drugiej:
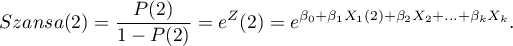
Iloraz Szans dla zmiennej  wyraża się wówczas wzorem:
wyraża się wówczas wzorem:
![LaTeX \begin{displaymath}
\begin{array}{lll}
OR_1(2)/(1) &=&\frac{Szansa(2)}{Szansa(1)}=\frac{e^{\beta_0+\beta_1X_1(2)+\beta_2X_2+...+\beta_kX_k}}{e^{\beta_0+\beta_1X_1(1)+\beta_2X_2+...+\beta_kX_k}}\\
&=& e^{\beta_0+\beta_1X_1(2)+\beta_2X_2+...+\beta_kX_k-[\beta_0+\beta_1X_1(1)+\beta_2X_2+...+\beta_kX_k]}\\
&=& e^{\beta_1X_1(2)-\beta_1X_1(1)}=e^{\beta_1[X_1(2)-X_1(1)]}=\\
&=& \left(e^{\beta_1}\right)^{[X_1(2)-X_1(1)]}.
\end{array}
\end{displaymath}](/lib/exe/fetch.php?media=wiki:latex:/img5e7d555cf6560897adceb6c87ea41a56.png)
Przykład
Jeśli zmienną niezależną jest wiek wyrażony w latach, to różnica pomiędzy sąsiadującymi kategoriami wieku np. 25 lat i 26 lat wynosi 1 rok 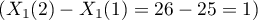 . Wówczas otrzymamy jednostkowy Iloraz Szans:
. Wówczas otrzymamy jednostkowy Iloraz Szans:
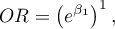 który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 1 rok.
który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 1 rok.
Iloraz szans wyliczony dla niesąsiadujących kategorii zmiennej wiek np. 25 lat i 30 lat będzie pięcioletnim Ilorazem Szans, ponieważ różnica 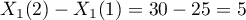 . Wówczas otrzymamy pięcioletni Iloraz Szans:
. Wówczas otrzymamy pięcioletni Iloraz Szans:
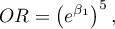 który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 5 lat.
który mówi o ile zmieni się szansa na wystąpienie wyróżnionej wartości gdy wiek zmieni się o 5 lat.
Uwaga!
Jeśli analizę przeprowadzamy dla modelu innego niż liniowy, lub uwzględniamy interakcję, wówczas na podstawie ogólnego wzoru możemy wyliczyć odpowiedni Ilorazu Szans zmieniając formułę wyrażającą  .
.
Przykład c.d. (plik zadanie.pqs)
Przykład c.d. (wada.pqs)
statpqpl/wielowympl/logistpl/orpl.txt · ostatnio zmienione: 2021/01/07 22:58 (edycja zewnętrzna)
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

