PQStat - Baza Wiedzy

The Odds Ratio

Individual Odds Ratio

On the basis of many coefficients, for each independent variable in the model an easily interpreted measure is estimated, i.e. the individual Odds Ratio: $\begin{displaymath} OR_i=e^{\beta_i}. \end{displaymath}$

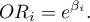
The received Odds Ratio expresses the change of the odds for the occurrence of the distinguished value (1) when the independent variable grows by 1 unit. The result is corrected with the remaining independent variables in the model so that it is assumed that they remain at a stable level while the studied variable is growing by 1 unit.

The OR value is interpreted as follows:

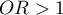$OR >1$ means the stimulating influence of the studied independent variable on obtaining the distinguished value (1), i.e. it gives information about how much greater are the odds of the occurrence of the distinguished value (1) when the independent variable grows by 1 unit.
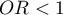$OR <1$ means the destimulating influence of the studied independent variable on obtaining the distinguished value (1), i.e. it gives information about how much lower are the odds of the occurrence of the distinguished value (1) when the independent variable grows by 1 unit.
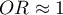$OR\approx1$ means that the studied independent variable has no influence on obtaining the distinguished value (1).

Odds Ratio - the general formula

The PQStat program calculates the individual Odds Ratio. Its modification on the basis of a general formula makes it possible to change the interpretation of the obtained result.

The Odds Ratio for the occurrence of the distinguished state in a general case is calculated as the ratio of two odds. Therefore for the independent variable 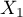$X_1$ for $Z$ expressed with a linear relationship we calculate:

the odds for the first category: $\begin{displaymath} Odds(1)=\frac{P(1)}{1-P(1)}=e^Z(1)=e^{\beta_0+\beta_1X_1(1)+\beta_2X_2+...+\beta_kX_k}, \end{displaymath}$

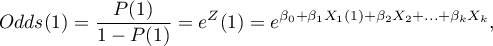
the odds for the second category:

$\begin{displaymath} Odds(2)=\frac{P(2)}{1-P(2)}=e^Z(2)=e^{\beta_0+\beta_1X_1(2)+\beta_2X_2+...+\beta_kX_k}. \end{displaymath}$

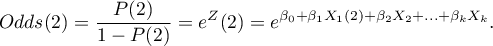
The Odds Ratio for variable 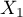$X_1$ is then expressed with the formula:

$\begin{displaymath} \begin{array}{lll} OR_1(2)/(1) &=&\frac{Odds(2)}{Odds(1)}=\frac{e^{\beta_0+\beta_1X_1(2)+\beta_2X_2+...+\beta_kX_k}}{e^{\beta_0+\beta_1X_1(1)+\beta_2X_2+...+\beta_kX_k}}\\ &=& e^{\beta_0+\beta_1X_1(2)+\beta_2X_2+...+\beta_kX_k-[\beta_0+\beta_1X_1(1)+\beta_2X_2+...+\beta_kX_k]}\\ &=& e^{\beta_1X_1(2)-\beta_1X_1(1)}=e^{\beta_1[X_1(2)-X_1(1)]}=\\ &=& \left(e^{\beta_1}\right)^{[X_1(2)-X_1(1)]}. \end{array} \end{displaymath}$

Example

If the independent variable is age expressed in years, then the difference between neighboring age categories such as 25 and 26 years is 1 year 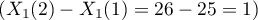$\left(X_1(2)-X_1(1)=26-25=1\right)$ . In such a case we will obtain the individual Odds Ratio:

$\begin{displaymath}OR=\left(e^{\beta_1}\right)^1,\end{displaymath}$

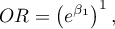
which expresses the degree of change of the odds for the occurrence of the distinguished value if the age is changed by 1 year.

The odds ratio calculated for non-neighboring variable categories, such as 25 and 30 years, will be a five-year Odds Ratio, because the difference 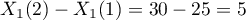$X_1(2)-X_1(1)=30-25=5$ . In such a case we will obtain the five-year Odds Ratio:

$\begin{displaymath}OR=\left(e^{\beta_1}\right)^5,\end{displaymath}$

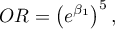
which expresses the degree of change of the odds for the occurrence of the distinguished value if the age is changed by 5 years.

Note

If the analysis is made for a non-linear model or if interaction is taken into account, then, on the basis of a general formula, we can calculate an appropriate Odds Ratio by changing the formula which expresses $Z$ .

EXAMPLE cont. (task.pqs file)

EXAMPLE cont. (anomaly.pqs file)

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

The Odds Ratio

Narzędzia strony