Narzędzia użytkownika
Narzędzia witryny
Jesteś tutaj: PQStat - Baza Wiedzy » PQStat - Statystyka » Modele wielowymiarowe » ANOVA czynnikowa - GLM
Pasek boczny
statpqpl:wielowympl:anovaglm
ANOVA czynnikowa - GLM
Okno z ustawieniami opcji ANOVA czynnikowa GLM wywołujemy poprzez menu Statystyka→Modele wielowymiarowe→ANOVA czynnikowa GLM
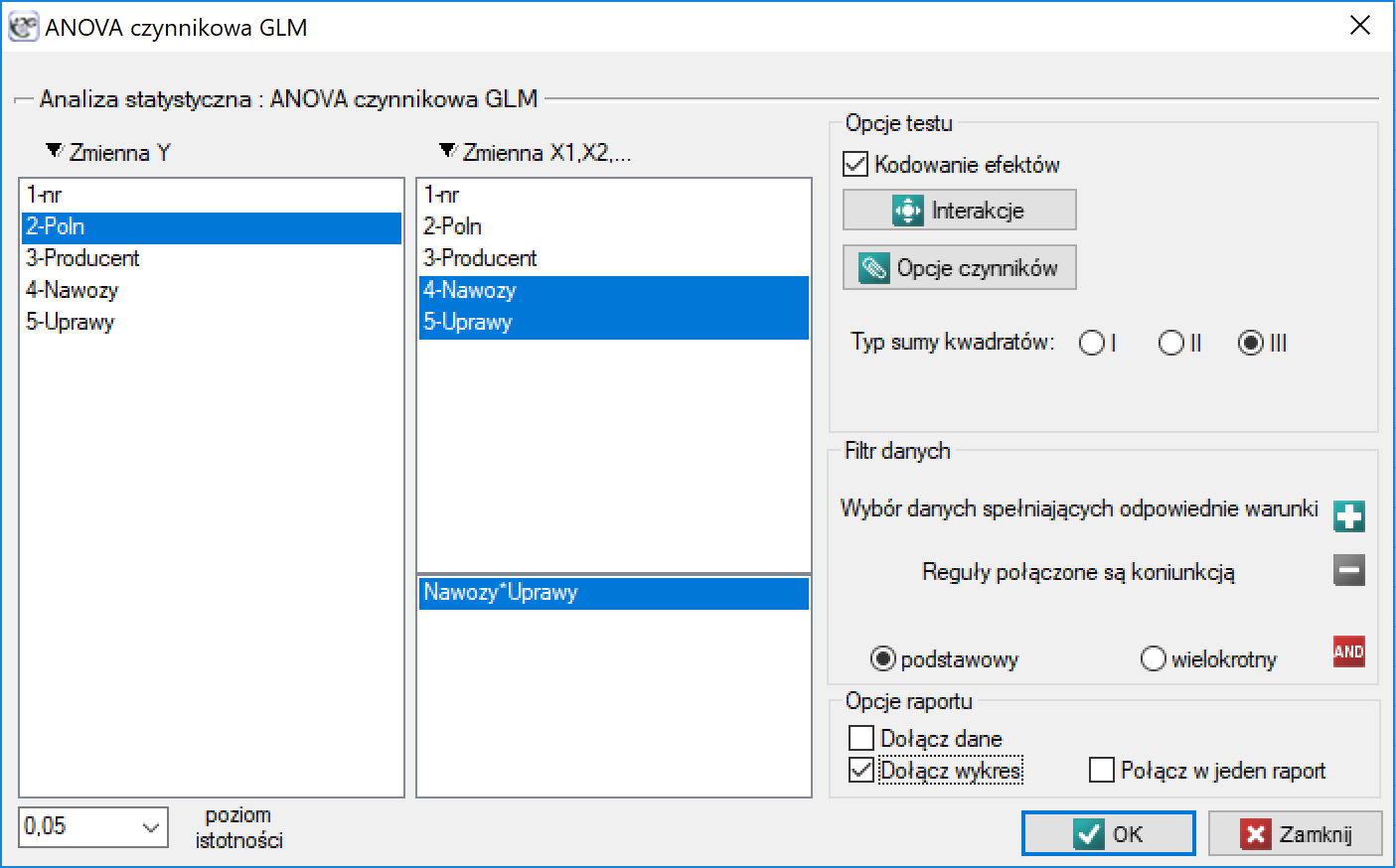

 Czynnikowa analiza wariancji GLM jest rozszerzeniem jednoczynnikowej analizy wariancji (ANOVA) dla grup niezależnych oraz liniowej regresji wielorakiej. Skrót GLM (ang. general linear model) czytamy jako Ogólny Model Liniowy. Analiza GLM polega zwykle na wykorzystaniu modeli regresji liniowej w wyliczaniu różnych złożonych porównań ANOVA.
Czynnikowa analiza wariancji GLM jest rozszerzeniem jednoczynnikowej analizy wariancji (ANOVA) dla grup niezależnych oraz liniowej regresji wielorakiej. Skrót GLM (ang. general linear model) czytamy jako Ogólny Model Liniowy. Analiza GLM polega zwykle na wykorzystaniu modeli regresji liniowej w wyliczaniu różnych złożonych porównań ANOVA.
Przykład
Przykład równoważnych analiz, które mogą być przeprowadzone poprzez GLM. Analizy zawarte w poszczególnych wierszach tabeli są równoważne w tym sensie, że ich wyniki są tożsame, choć nie muszą być identyczne.
Badanie dotyczy dochodu pewnej grupy osób. O badanych osobach mamy pewne dodatkowe informacje typu: płeć i wykształcenie.
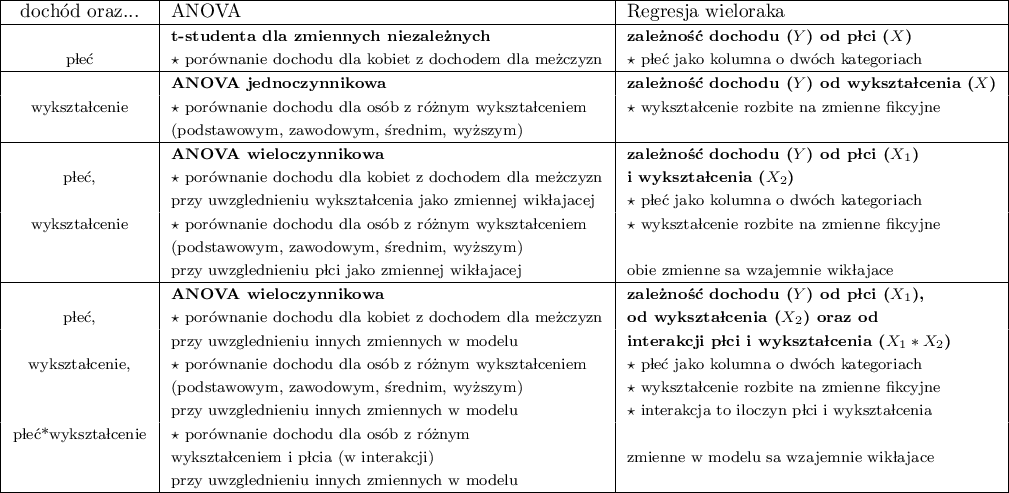
Analiza GLM może być wykorzystana w każdym z powyższych przypadków, ponieważ jednak analiza regresji wielorakiej podobnie jak jednoczynnikowa ANOVA zostały omówione w oddzielnych rozdziałach, w tym rozdziale przedstawimy wykorzystanie GLM w ANOVA wieloczynnikowa.
ANOVA czynnikowa jest takim rodzajem analizy wariancji, w którym możemy wykorzystać zarówno jedną jak i wiele czynników by wyodrębnić porównywane grupy. W analizie mogą brać udział również takie zmienne, które są interakcją wskazanych czynników. Gdy ANOVA zawiera więcej czynników niż jeden, wówczas czynniki te są wobec siebie uwikłane.
Wpływ czynników wikłających
Pomimo, że wszystkie czynniki biorące udział w analizie są wobec siebie uwikłane, to ich wpływ na istotność poszczególnych czynników można kontrolować. Istnieją trzy sposoby, przy pomocy których badając istotność poszczególnych czynników można uwzględniać wpływ zmiennych wikłających. Zależą one od sposobu wyznaczania sumy kwadratów:
- Sumy kwadratów typu I
Sumy kwadratów typu I zależą od kolejności w jakiej w modelu znajdują się poszczególne czynniki. Ten rodzaj sumy kwadratów powoduje, że istotność czynnika który interpretujemy jest korygowana o te zmienne, których kolejność w modelu była wcześniejsza, pozostałe zmienne w modelu wpływają jedynie pośrednio na wynik analizy. Na przykład: jeśli w modelu umieszczamy czynniki we wskazanej kolejności:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 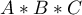 ,
, 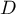 , wówczas istotność dla czynnika
, wówczas istotność dla czynnika  uwzględnia cały model (poprzez sumy kwadratów dla błędu) ale jako zmienne wikłające wykorzystywane są wprost tylko czynniki:
uwzględnia cały model (poprzez sumy kwadratów dla błędu) ale jako zmienne wikłające wykorzystywane są wprost tylko czynniki:  ,
,  ,
,  ,
,  .
.
Sumy kwadratów dla czynnika  wylicza się wówczas następująco:
wylicza się wówczas następująco:
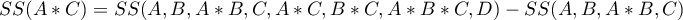
Stosowanie sumy kwadratów typu I
Wskazania: Kiedy badanie jest w pełni zbalansowane, z równymi lub proporcjonalnymi licznościami poszczególnych kategorii, również wtedy, gdy występują interakcje.
Przeciwwskazania: Kiedy badanie jest niezbalansowane (różne liczności poszczególnych kategorii) i/lub występują interakcje.
- Sumy kwadratów typu II
Ten rodzaj sumy kwadratów powoduje, że istotność czynnika który interpretujemy jest korygowana o te zmienne, których rząd jest taki sam lub niższy, pozostałe zmienne w modelu wpływają jedynie pośrednio na wynik analizy. Na przykład: jeśli w modelu umieszczamy czynniki:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 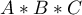 ,
, 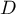 , wówczas istotność dla czynnika
, wówczas istotność dla czynnika  uwzględnia cały model (poprzez sumy kwadratów dla błędu) ale jako zmienne wikłające wykorzystywane są wprost zmienne pierwszego rzędu:
uwzględnia cały model (poprzez sumy kwadratów dla błędu) ale jako zmienne wikłające wykorzystywane są wprost zmienne pierwszego rzędu:  ,
,  ,
,  ,
, 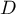 oraz wszystkie pozostałe zmienne drugiego rzędu:
oraz wszystkie pozostałe zmienne drugiego rzędu:  ,
,  .
.
Sumy kwadratów dla czynnika  wylicza się wówczas następująco:
wylicza się wówczas następująco:
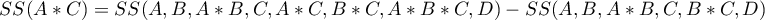
Stosowanie sumy kwadratów typu II
Wskazania: Kiedy badanie jest w pełni zbalansowane, z równymi lub proporcjonalnymi licznościami poszczególnych kategorii, również wtedy, gdy występują interakcje.
Przeciwwskazania: Kiedy badanie jest niezbalansowane (różne liczności poszczególnych kategorii) i/lub występują interakcje.
- Sumy kwadratów typu III
Zalecamy stosować ten rodzaj kodowania, gdy wybrane jest kodowanie efektów.
Ten rodzaj sumy kwadratów powoduje, że istotność czynnika który interpretujemy jest korygowana o wszystkie pozostałe zmienne w modelu. Na przykład: jeśli w modelu umieszczamy czynniki:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 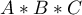 ,
, 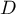 , wówczas istotność dla zmiennej
, wówczas istotność dla zmiennej  uwzględnia cały model (poprzez sumy kwadratów dla błędu) a jako zmienne wikłające wykorzystywane są wprost wszystkie czynniki za wyjątkiem badanego:
uwzględnia cały model (poprzez sumy kwadratów dla błędu) a jako zmienne wikłające wykorzystywane są wprost wszystkie czynniki za wyjątkiem badanego:  ,
,  ,
,  ,
,  ,
,  ,
, 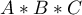 ,
,  ,.
,.
Sumy kwadratów dla czynnika  wylicza się wówczas następująco:
wylicza się wówczas następująco:
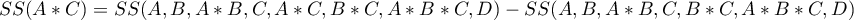
Stosowanie sumy kwadratów typu III
Wskazania: Kiedy badanie jest zbalansowane lub niezbalansowane, również wtedy, gdy występują interakcje.
Przeciwwskazania: Kiedy badanie zawiera podklasy o brakujących obserwacjach.
W PQStat domyślnie wybrane są sumy kwadratów typu III, ze względu na ich uniwersalność. Domyślnie zaznaczona jest też opcja kodowanie efektów opisana w rozdziale Przygotowanie zmiennych do analizy. Należy pamiętać, że wybór odpowiedniego kodowania wpływa zarówno na interpretację współrzędnych modelu jak i na istotność poszczególnych czynników w ANOVA czynnikowa - szczególnie przy niezbalansowanych układach.
Podstawowe warunki stosowania:
- pomiar na skali interwałowej,
- próby pochodzą z populacji o rozkładzie normalnym normalność zmiennych bądź reszt modelu),
- równość wariancji badanych zmiennych porównywanych populacji.
ANOVA czynnikowa wymaga by czynniki dzieliły się na poszczególne kategorie (tj. niezależne populacje) np. czynnik  : płeć dzielimy na męską i żeńską, czynnik
: płeć dzielimy na męską i żeńską, czynnik  : wykształcenie na podstawowe, zawodowe, średnie i wyższe. Interakcja czynnika
: wykształcenie na podstawowe, zawodowe, średnie i wyższe. Interakcja czynnika  jest również dzielona na kategorie, w tym przypadku kategorii uzyskamy osiem:
jest również dzielona na kategorie, w tym przypadku kategorii uzyskamy osiem:
1) kategoria żeńska z wykształceniem podstawowym,
2) żeńska z wykształceniem zawodowym,
3) żeńska z wykształceniem średnim,
4) żeńska z wykształceniem wyższym,
5) kategoria męska z wykształcniem podstawowym,
6) męska z wykształceniem zawodowym,
7) męska z wykształceniem średnim,
8) męska z wykształceniem wyższym.
Analiza typu ANOVA i modele regresji traktowane są równoważnie, i w ogólnym przypadku ich hipotezy są zbieżne. Hipotezy dla efektów głównych  i
i  i efektu interakcji
i efektu interakcji  przedstawimy w obu tych ujęciach. W interpretacji tych hipotez należy pamiętać, że hipotezy dla danych czynników korygowane są o te z pozostałych czynników, które dana analiza uwzględnia.
przedstawimy w obu tych ujęciach. W interpretacji tych hipotez należy pamiętać, że hipotezy dla danych czynników korygowane są o te z pozostałych czynników, które dana analiza uwzględnia.
Podejście ANOVA
Hipotezy dla czynnika  :
:
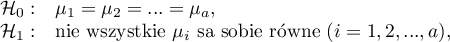
gdzie:
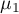 ,
,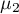 ,…,
,…,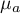
 średnie czynnika
średnie czynnika  dla poszczególnych jego kategorii.
dla poszczególnych jego kategorii.
Hipotezy dla czynnika  :
:
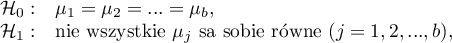
gdzie:
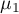 ,
,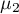 ,…,
,…,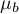
 średnie czynnika
średnie czynnika  dla poszczególnych jego kategorii.
dla poszczególnych jego kategorii.
Hipotezy dla interakcji czynników  :
:
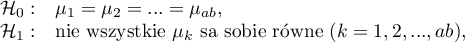
gdzie:
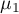 ,
,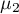 ,…,
,…,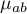
 średnie interakcji czynników
średnie interakcji czynników  dla poszczególnych ich kategorii.
dla poszczególnych ich kategorii.
Podejście regresyjne
Podejście modelowe zakłada działanie modelu regresji
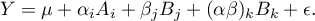
gdzie:
 - zmienna zależna, objaśniana przez model,
- zmienna zależna, objaśniana przez model,
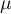 - średnia ogólna zmiennej
- średnia ogólna zmiennej  (o ile zastosowano kodowanie efektów)
(o ile zastosowano kodowanie efektów)
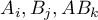 - czynniki - zmienne niezależne, objaśniające,
- czynniki - zmienne niezależne, objaśniające,
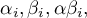 - parametry,
- parametry,
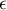 - składnik losowy (reszta modelu).
- składnik losowy (reszta modelu).
Hipotezy dla czynnika  :
:
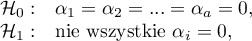
Hipotezy dla czynnika  :
:
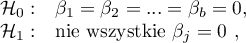
Hipotezy dla interakcji czynników  :
:
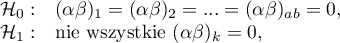
Kodowanie
Uzyskiwane wyniki analiz (w szczególności budowanego modelu regresji) oraz interpretacja hipotez zależą również od sposobu kodowania. Program PQStat oferuje kodowanie zero-jedynkowe i kodowanie efektów. Dokładny opis kodowania można znaleźć w rozdziale Przygotowanie zmiennych do analizy w modelach wielowymiarowych. Domyślnie program wybiera kodowanie efektów. Odznaczenie tej opcji jest równoważne z wybraniem kodowania zero-jedynkowego.
Uwaga!
W przypadku stosowaniu sumy kwadratów typu III, gdy występują interakcje, wskazane jest stosowanie kodowania efektów.
Aby zwiększyć plon roślin uprawnych, opracowuje się nawozy według coraz nowszych technologii. Na podstawie przeprowadzonego eksperymentu badacze chcą się dowiedzieć, która z trzech mieszanek nowych nawozów jest najbardziej skuteczna. Uprawy były prowadzone przez dwa różne gospodarstwa rolne i dotyczyły zasiewu pszenicy, żyta, owsa i jęczmienia. Plon podawano w % (w porównaniu do plonu uzyskanego bez nawożenia).
W pierwszej kolejności chcemy sprawdzić czy:
1) H0: Średnie plony uzyskane przy zastosowaniu nawożenia mieszanką X są takie same jak uzyskane przy nawożeniu mieszanką Y i takie same jak przy nawożeniu mieszanką Z (niezależnie od gospodarstwa prowadzącego uprawę).
Ponadto, choć jest to w tym przypadku miej interesujące, sprawdzimy czy:
2) H0: Średnie plony uzyskane w gospodarstwie 1 są takie same jak w gospodarstwie drugim (niezależnie od mieszanki stosowanego nawozu).
Równoważnie hipotezy te można zapisać korzystając z podejścia regresyjnego:
1) H0: Współczynniki określające zmianę uzyskanego plonu przy zmianie stosowanego nawożenia są zerowe (niezależnie od gospodarstwa prowadzącego uprawę).
2) H0: Współczynnik określający zmianę uzyskanego plonu przy zmianie gospodarstwa prowadzącego uprawę jest zerowy (niezależnie od mieszanki stosowanego nawozu).
W drugiej kolejności stosując GLM sprawdzimy czy:
3) H0: Średnie plony uzyskane z uprawy poszczególnych zbóż są takie same gdy stosujemy różny sposób nawożenia.
Hipotezy 1) i 2)
Podejście ANOVA
Analizę przeprowadzimy stosując trzeci typ sumy kwadratów i kodowanie efektów.
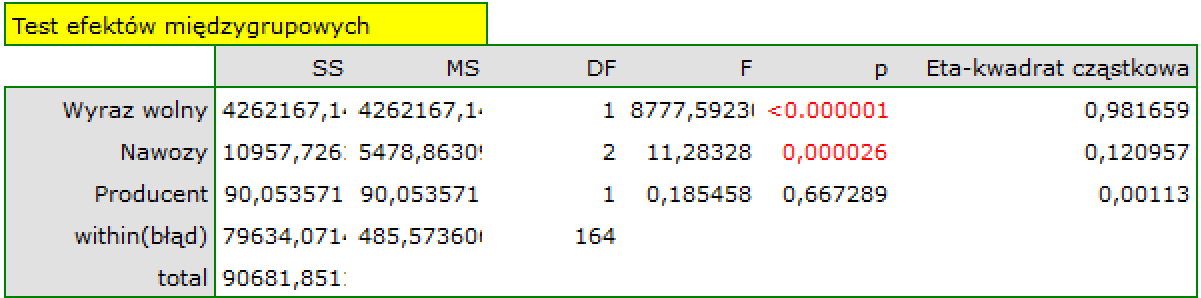
Obserwujemy istotne statystycznie różnice pomiędzy plonem uzyskanym przy zastosowaniu różnych mieszanek nawozów (p=0.000026). Zastosowana mieszanka nawozów tłumaczy zmienność w uzyskanym plonie w około 12% o czym świadczy wartość cząstkowej Eta-kwadrat. Uzyskane plony nie zależą natomiast od tego w jakim gospodarstwie prowadzono uprawy (p=0.667289, Eta-kwadrat cząstkowe = 0,1%).
Po wybraniu średnich obserwowanych lub oczekiwanych w oknie Opcji czynników, różnice te możemy przedstawić graficznie na wykresach obrazujących średnie plony przy stosowaniu poszczególnych mieszanek nawozów. Dokładne wartości średnich możemy odczytać z tabeli statystyk opisowych.
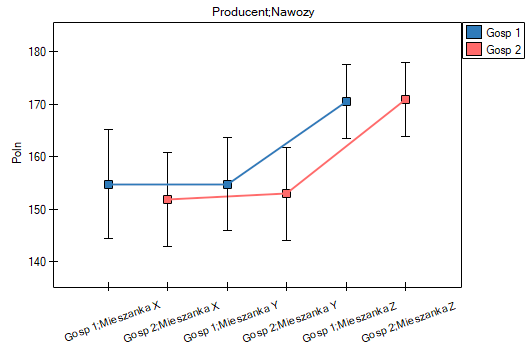
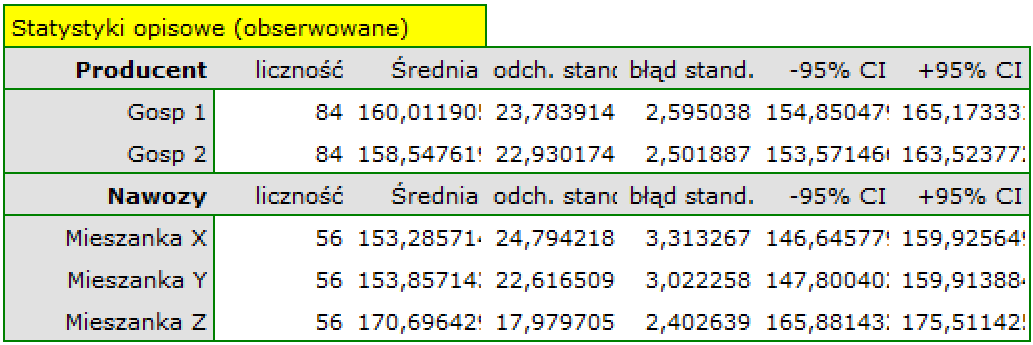
To, gdzie różnice są zlokalizowane możemy sprawdzić stosując testy post-hoc. Test post-hoc NIR Fishera wskazuje, iż najkorzystniejsze rezultaty przynosi stosowanie mieszanki Z – uzyskany plony stanowi średnio 170,7% plonu, który uzyskano by nie stosując nawożenia. Pozostałe mieszani nie różnią się istotnie statystycznie wielkością uzyskanego plonu. Ponieważ w modelu jednoczesnej analizie poddawano gospodarstwo w którym prowadzone były uprawy, możemy powiedzieć, że przewaga mieszanki Z jest niezależna od tego, w którym gospodarstwie wykonano zasiew.
Podejście regresyjne
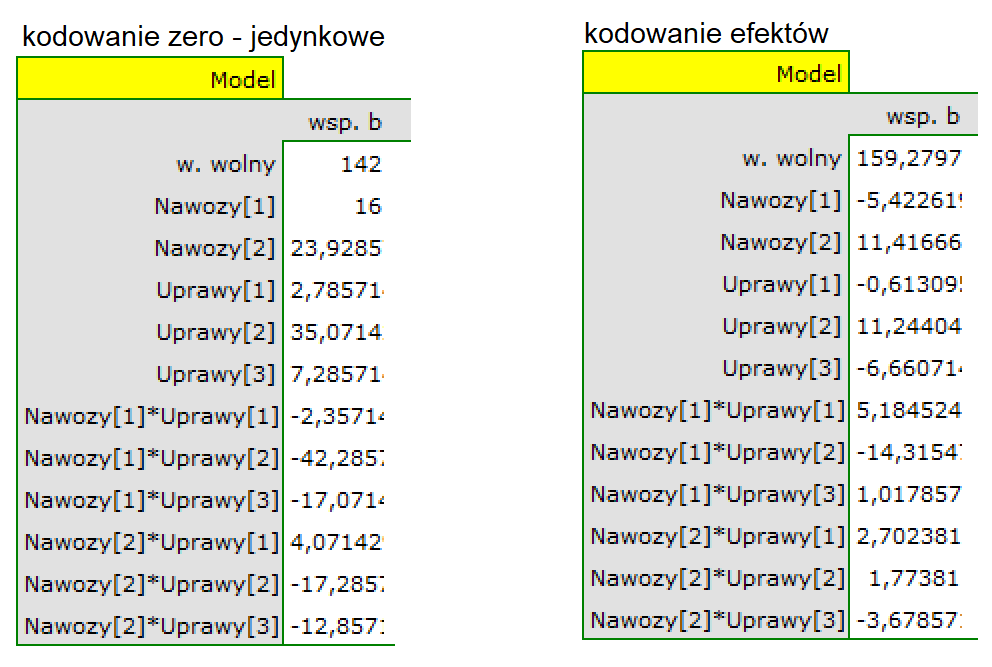
Analogiczną interpretację uzyskamy posługując się modelem regresji, choć tutaj interpretacja jest nieco trudniejsza. Trudność wynika z konieczności ustalenia sposobu kodowania i wyboru kategorii odniesienia. Przyjrzyjmy się najpierw wynikom otrzymanym przy kodowaniu zero-jedynkowym, które możemy uzyskać odznaczając opcję kodowania efektów. Analiza automatycznie przyjęła alfabetycznie pierwszy poziom jako poziom odniesienia. Dla nawozów poziomem tym była mieszanka X, dla gospodarstw było to gospodarstwo 1.


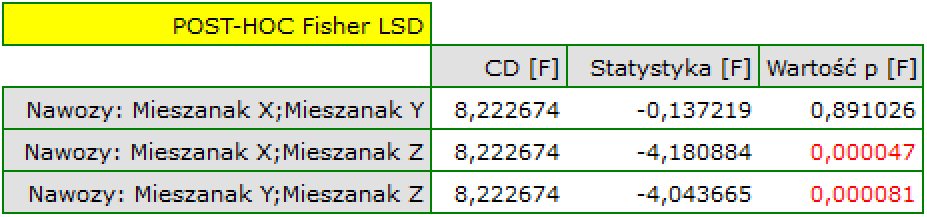
Analiza współczynników modelu przypomina analizę testów post-hoc, z tą różnicą, że porównujemy wyłącznie do kategorii odniesienia. Jeśli więc wszystkie mieszanki nawozów porównamy do mieszanki X możemy zauważyć, że jedynie stosując mieszankę Z uzyskano istotnie wyższe wyniki (p= 0.000047). Wyniki te są wyższe o 17.410714 (przypominam, że średnie wynosiły odpowiednio (153.285714 – dla mieszanki X, 170.696429 – dla mieszanki Z). Porównując gospodarstwa sprawa jest prosta, gdyż mamy do porównania tylko dwa gospodarstwa i uzyskany wynik jest wynikiem porównania gospodarstwa 2 z gospodarstwem 1, które to stanowiło kategorię odniesienia. Tym razem uzyskana różnica była niewielka (-1.464286) i nieistotna statystycznie (0.667289).
Stosując kodowanie efektów również wybieramy kategorię odniesienia, ale wielkość współczynników i ich istotność nie jest odnoszona do wybranej kategorii odniesienia ale do średniej ogólnej uzyskanego plonu, zapisanej w modelu jako wyraz wolny (159.279762).
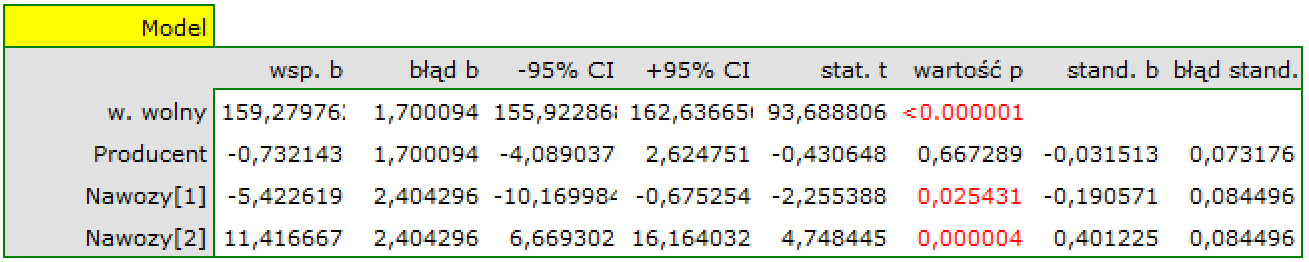
W porównaniu do średniej ogólnej znajdujemy sporo różnic: plon uzyskany przy nawożeniu mieszanką Y jest o 5.422619 niższy niż średnia ogólna, a mieszanką Z o 11.416667 wyższy. Obie różnice są istotne statystycznie.
Niepodważalną zaletą budowania modelu regresyjnego jest możliwość wykorzystania jego formuły w przewidywaniu uzyskanych plonów. Zbudowane modele prezentują się następująco:
Dla kodowania zero-jedynkowego:
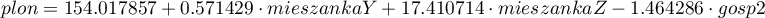
Dla kodowania efektów:
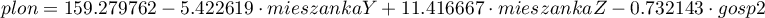
By móc zastosować wybrany model w prognozowaniu należy udać się do menu regresja wieloraka – predykcja i na podstawie nowych danych dokonać predykcji. Przy czym przygotowanie danych zależy od sposobu ich kodowania.
Na podstawie wszystkich uzyskanych wyników nie podejrzewamy by wielkość plonu była zależna od interakcji między rodzajami stosowanych nawozów a gospodarstwem prowadzącym uprawy. Najczęściej występowanie interakcji widoczne jest na wykresie w postaci wyraźnie przecinających się linii. Tu obie linie były prawie równoległe i na tyle bliskie sobie, że różnica między gospodarstwami była nieistotna statystycznie. Mimo, że przecinające się linie najczęściej świadczą o występowaniu interakcji należy pamiętać, żę gdy linie znajdują się blisko siebie ich przypadkowe przecięcie jest bardzo prawdopodobne, w efekcie tego interakcja nie będzie istotna statystycznie. Dla pewności sprawdzimy jednak, czy w naszym przypadku występuje interakcja. W tym celu obie zmienne wybierzemy raz jeszcze w oknie interakcji i przeniesiemy do listy interakcji umieszczonej po prawej stronie okna a następnie powtórzymy analizę.
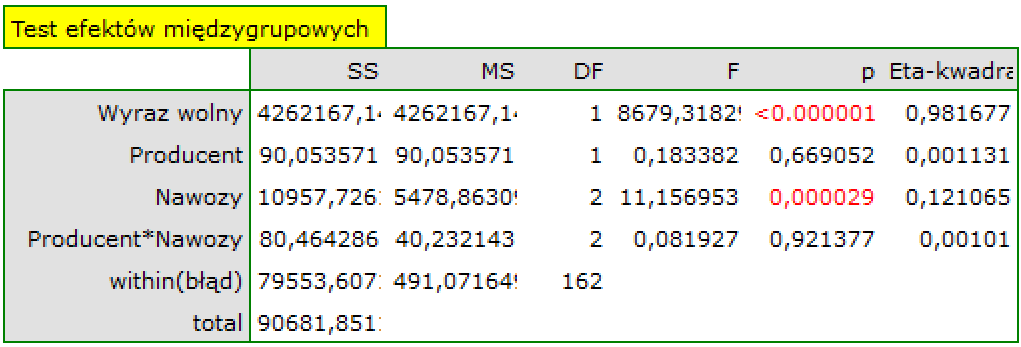
Uzyskany wynik potwierdził nasze przypuszczenia o braku istotnej interakcji (p=0.921377). W tym wypadku zaleca się więc stosowanie modelu prostszego, tzn. pozbawionego interakcji.
Hipoteza 3)
Z odmienną sytuacją zetkniemy się badając wielkość uzyskanego plonu w zależności od stosowanej dawki nawozu oraz w zależności od rodzaju uprawianego zboża.
Wykonamy analizę która oprócz efektów głównych uwzględnia interakcje.
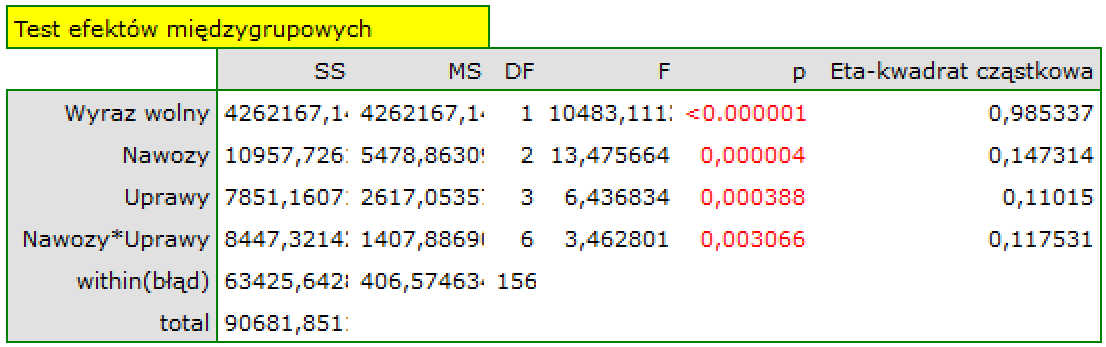
Ponieważ interakcje w zbudowanym modelu są istotne statystycznie (p=0.003066), to właśnie model z interakcjami powinniśmy stosować i opis uzyskanych wyników skupić właśnie na tej interakcji.
W podejściu ANOVA hipoteza odnosząca się do interakcji dotyczy wszystkich możliwych par średnich, tzn.:
H0: Średnie plony uzyskane przy nawożeniu pszenicy mieszanką X są takie same jak przy nawożeniu pszenicy mieszanką Y i takie same jak przy nawożeniu pszenicy mieszanką Z i takie same jak przy nawożeniu żyta mieszanką X i takie same jak przy nawożeniu żyta mieszanką Y i takie same jak przy nawożeniu żyta mieszanką Z i takie same jak przy nawożeniu owsa mieszanką X i takie same jak przy nawożeniu owsa mieszanką Y i takie same jak przy nawożeniu owsa mieszanką Z i takie same jak przy nawożeniu jęczmienia mieszanką X i takie same jak przy nawożeniu jęczmienia mieszanką Y i takie same jak przy nawożeniu jęczmienia mieszanką Z.
W podejściu regresyjnym powiemy, że:
H0: Współczynniki określające zmianę uzyskanego plonu przy zmianie stosowanego nawożenia i zmianie rodzaju uprawy są zerowe.
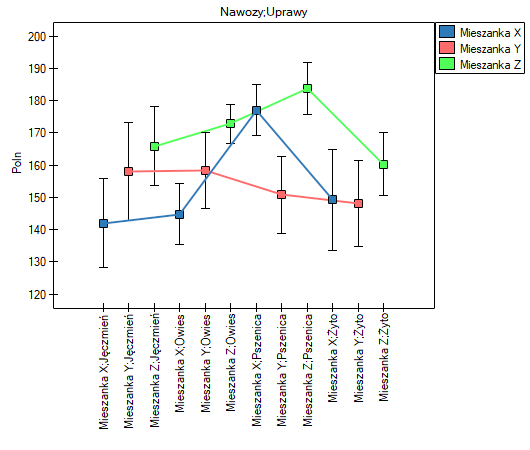
Na podstawie wykresu (oraz średnich zapisanych w tabeli) widzimy iż zdecydowanie najlepsze plony przynosi mieszanka Z, niezależnie od rodzaju uprawianego zboża.

Natomiast mieszanka X i mieszanka Y uzyskują gorsze plony od mieszanki Z i dodatkowo zachodzi między nimi efekt interakcji. Przejawia się ona tym, że uprawa pszenicy przynosi nietypowo wysoki plon w przypadku zastosowania mieszanki X w porównaniu do plonu pszenicy uzyskanego przy nawożeniu Y, podczas gdy uprawa jęczmienia i owsa lepiej plonują, gdy stosowana jest mieszanka Y. Dokładniej uzyskane różnice możemy sprawdzić wykonując testy post-hoc. Fragment tego raportu zamieszczono poniżej:
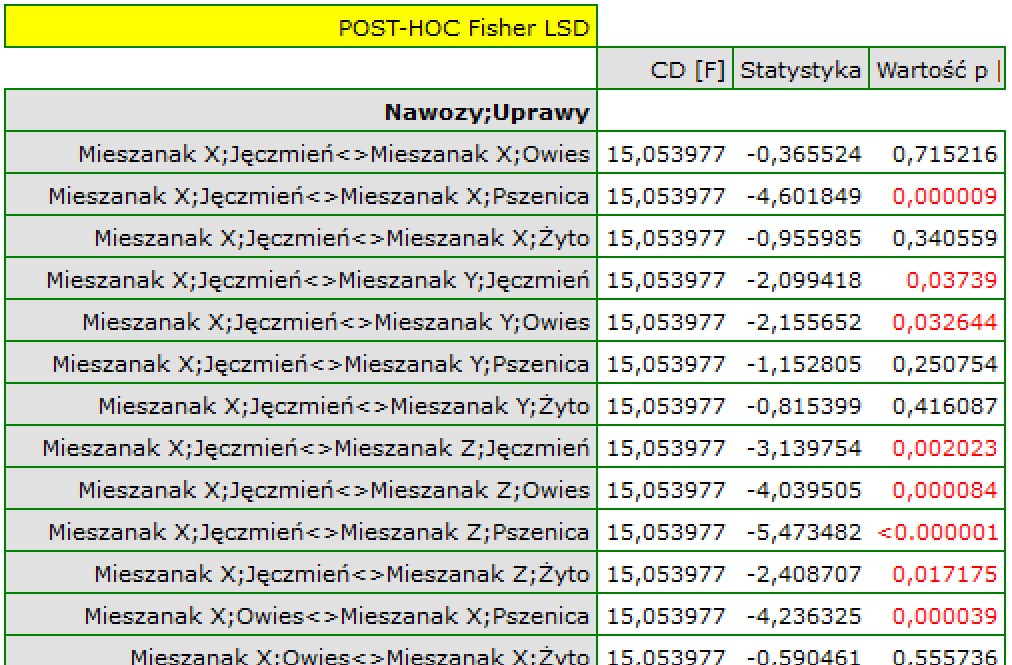
Wynik testu post-hoc Fishera jest obszerny i potwierdza dużą i istotną statystycznie przewagę uzyskanego plonu przy stosowaniu mieszanki Z dla dowolnych upraw i mieszanki Y dla uprawy pszenicy.
Współczynniki modelu regresji możemy wykorzystać do prognozy poprzez menu regresja wieloraka – predykcja pamiętając, by w zależności od wybranego modelu odpowiednio zakodować nowe dane.
SPRAWDZENIE ZAŁOŻEŃ
Sprawdzenie głównych założeń będzie polegało na porównaniu wariacji oraz wizualnym określeniu normalności reszt modelu.
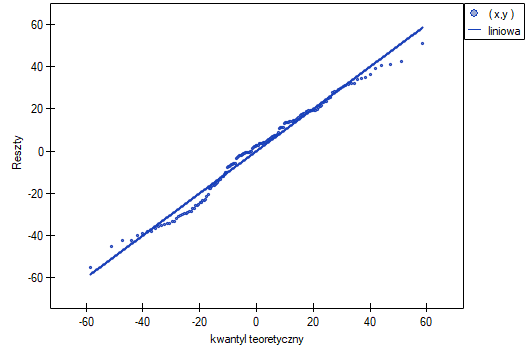
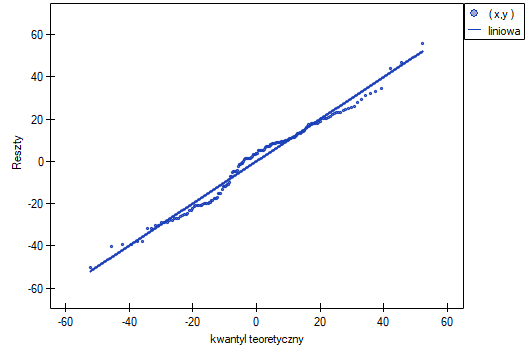
Wykres normalności reszt modelu typu Q-Q dla pierwszej oraz dla drugiej analizy przedstawia reszty modelu dobrze rozlokowane wokół prostej, co świadczy o dobrym dopasowaniu reszt do rozkładu normalnego. Porównaniu wariancji służy test Levenea lub Browna-Forsythea. W przypadku tych testów możemy założyć, że uzyskane wyniki nie są jednoznaczne i są na pograniczu równości wariancji.
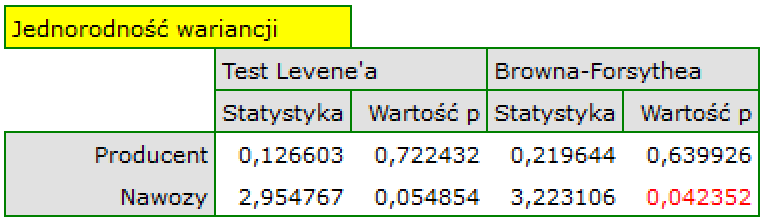
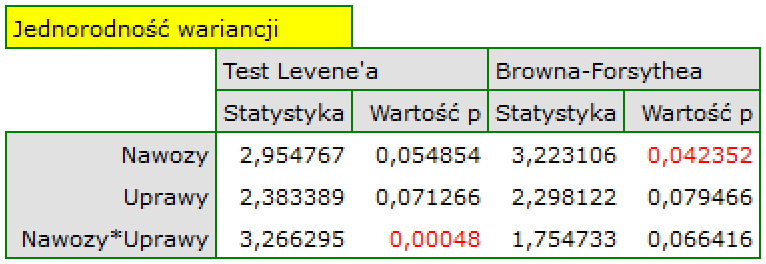
statpqpl/wielowympl/anovaglm.txt · ostatnio zmienione: 2022/01/23 21:30 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

