PQStat - Baza Wiedzy

Sferyczność Mauchly’a

Założenie sferyczności jest podobne ale silniejsze niż założenie równości wariancji. Jest ono spełnione, jeśli wariancje dla różnic pomiędzy parami powtarzanych pomiarów są takie same. Zwykle w zastępstwie założenia o sferyczności rozważa się prostszy, ale bardziej rygorystyczny warunek symetrii połączonej (ang. compound symmetry). Można tak postąpić ponieważ spełnienie warunku symetrii połączonej pociąga za sobą spełnienie założenia sferyczności.

Warunek symetrii połączonej zakłada symetrię w macierzy kowariancji, a zatem równość wariancji zmiennych (elementów głównej przekątnej macierzy kowariancji) oraz równość kowariancji (elementów poza główną przekątną macierzy kowariancji).

Naruszenie założenia sferyczności lub symetrii połączonej zmniejsza w nieuzasadniony sposób konserwatyzm testu F (ułatwia odrzucenie hipotezy zerowej).

Dla sprawdzenia założenia sferyczności używa się testu Mauchly’a (1940)¹⁾. Istotność wyniku (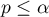 $p\le \alpha$ ) oznacza tu naruszenie założenia sferyczności.

Podstawowe warunki stosowania:

pomiar na skali interwałowej,
wielowymiarowy rozkład normalny lub normalność rozkładu każdej badanej zmiennej,
model zależny.

Hipotezy:

$\begin{array}{cl} \mathcal{H}_0: & \sigma_{diff(1)}=\sigma_{diff(2)}=...=\sigma_{diff(s)},\\ \mathcal{H}_1: & $nie wszystkie $\sigma_{diff(i)}$ są sobie równe $(i=1,2,...,s)$$, \end{array}$

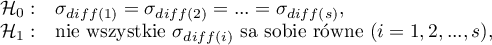
gdzie:

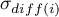$\sigma_{diff(i)}$ - populacyjna wariancja różnic pomiędzy $i$ -tą parą powtarzanych pomiarów,

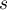$s$ - liczba par.

Wartość $W$ Mauchly’a definiowana jest następująco:

$\begin{displaymath} W=\frac{\prod_{j=1}^{k-1}\lambda_j}{\left(\frac{1}{k-1}\sum_{j=1}^{k-1}\lambda_j\right)^{k-1}}. \end{displaymath}$

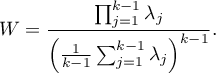
Statystyka testowa ma postać:

$\begin{displaymath} \chi^2=(f-1)(n-1)\ln W, \end{displaymath}$

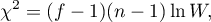
gdzie:

$f=\frac{2(k-1)^2+(k-1)+2}{6(k-1)(n-1)}$ ,

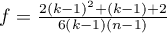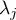$\lambda_j$ - wartość własna oczekiwanej macierzy kowariancji,

$k$ - liczba analizowanych zmiennych.

Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 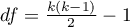$df=\frac{k(k-1)}{2}-1$ stopniami swobody.

Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

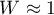Wartość $W\approx1$ oznacza spełnienie założenia sferyczności. W interpretacji wyników tego testu należy jednak pamiętać, że jest on wrażliwy na złamanie założenia normalności rozkładu.

Patrz przykład (plik ciśnienie.pqs)

¹⁾

Mauchly J. W. (1940), Significance test for sphericity of n-variate normal population. Annals of Mathematical Statistics, 11, 204-209

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Sferyczność Mauchly’a

Narzędzia strony