PQStat - Baza Wiedzy

Mauchly's sphericity

Sphericity assumption is similar but stronger than the assumption of equality of variance. It is met if the variances for the differences between pairs of repeated measurements are the same. Usually, the simpler but more stringent compound symmetry condition is considered in place of the sphericity assumption. This can be done because meeting the compounded symmetry condition entails meeting the sphericity assumption.

Compound symmetry condition assumes, symmetry in the covariance matrix, and therefore equality of variances (elements of the main diagonal of the covariance matrix) and equality of covariances (elements off the main diagonal of the covariance matrix).

Violating the assumption of sphericity or combined symmetry unduly reduces the conservatism of the F-test (makes it easier to reject the null hypothesis).

To check the sphericity assumption, the Mauchly test is used (1940)\cite{mauchly}. Statistical significance (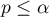 $p\le \alpha$ ) here implies a violation of the sphericity assumption.

Basic application conditions:

measurement on an interval scale,
multivariate normal distribution or normality of the distribution of each variable tested,
dependent model.

Hypotheses:

$\begin{array}{cl} \mathcal{H}_0: & \sigma_{diff(1)}=\sigma_{diff(2)}=...=\sigma_{diff(s)},\\ \mathcal{H}_1: & $not all $\sigma_{diff(i)}$ are equal $(i=1,2,...,s)$,$ \end{array}$

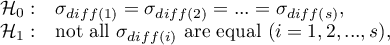
where:

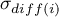$\sigma_{diff(i)}$ - population variance of differences between $i$ -th pair of repeated measurements,

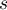$s$ - number of pairs.

Mauchly's $W$ value is defined as follows:

$\begin{displaymath} W=\frac{\prod_{j=1}^{k-1}\lambda_j}{\left(\frac{1}{k-1}\sum_{j=1}^{k-1}\lambda_j\right)^{k-1}}. \end{displaymath}$

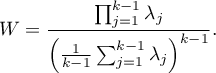
The test statistic has the form of:

$\begin{displaymath} \chi^2=(f-1)(n-1)\ln W, \end{displaymath}$

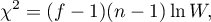
where:

$f=\frac{2(k-1)^2+(k-1)+2}{6(k-1)(n-1)}$ ,

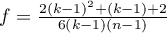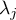$\lambda_j$ - eigenvalue of the expected covariance matrix,

$k$ - number of variables analyzed.

This statistic has asymptotically (for large sample) Chi-square distribution with 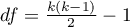$df=\frac{k(k-1)}{2}-1$ degrees of freedom.

The p-value, designated on the basis of the test statistic, is compared with the significance level $\alpha$ :

$\begin{array}{ccl} $ if $ p \le \alpha & \Longrightarrow & $ reject $ \mathcal{H}_0 $ and accept $ \mathcal{H}_1, \\ $ if $ p > \alpha & \Longrightarrow & $ there is no reason to reject $ \mathcal{H}_0. \\ \end{array}$

A value of 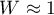$W\approx1$ is an indication that the sphericity assumption is met. In interpreting the results of this test, however, it is important to note that it is sensitive to violations of the normality assumption of the distribution.

EXAMPLE (pressure.pqs file)

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Mauchly's sphericity

Narzędzia strony