Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:porown2grpl:nparpl:z_nzalrpl
Test Z dla dwóch niezależnych proporcji
Test  dla dwóch niezależnych proporcji stosujemy w podobnych sytuacjach jak test chi-kwadrat (2x2), tzn. gdy mamy 2 niezależne próby o liczności
dla dwóch niezależnych proporcji stosujemy w podobnych sytuacjach jak test chi-kwadrat (2x2), tzn. gdy mamy 2 niezależne próby o liczności 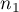 i
i 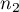 , w których możemy uzyskać 2 możliwe wyniki badanej cechy (jeden z nich to wynik wyróżniony o liczności
, w których możemy uzyskać 2 możliwe wyniki badanej cechy (jeden z nich to wynik wyróżniony o liczności 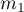 - w pierwszej próbie i
- w pierwszej próbie i 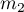 - w drugiej próbie). Dla prób tych możemy również wyznaczyć wyróżnione proporcje
- w drugiej próbie). Dla prób tych możemy również wyznaczyć wyróżnione proporcje 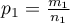 i
i 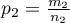 . Test ten służy do weryfikacji hipotezy, że wyróżnione proporcje
. Test ten służy do weryfikacji hipotezy, że wyróżnione proporcje 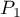 i
i 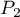 w populacjach, z których pochodzą próby są sobie równe.
w populacjach, z których pochodzą próby są sobie równe.
Podstawowe warunki stosowania:
- pomiar na skali nominalnej - ewentualne uporządkowanie kategorii nie jest brane pod uwagę,
- duża liczność.
Hipotezy:
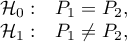
gdzie:
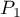 ,
, 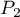 frakcja dla pierwszej i drugiej populacji.
frakcja dla pierwszej i drugiej populacji.
Statystyka testowa ma postać:
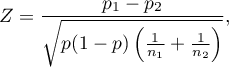
gdzie:
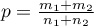 .
.
Zmodyfikowana o poprawkę na ciągłość statystyka testowa ma postać:
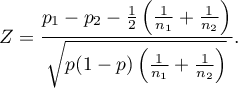
Statystyka bez korekcji na ciągłość jak i z tą korekcją ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

W programie oprócz różnicy proporcji wyliczana jest wartość wskaźnika NNT i/lub NNH.
NNT (ang. number needed to treat)  wskaźnik stosowany w medycynie, oznacza liczbę pacjentów, których trzeba poddać leczeniu przez określony czas, aby wyleczyć jedną osobę, która w innych okolicznościach nie wyzdrowiałaby. NNT wyliczane jest z wzoru:
wskaźnik stosowany w medycynie, oznacza liczbę pacjentów, których trzeba poddać leczeniu przez określony czas, aby wyleczyć jedną osobę, która w innych okolicznościach nie wyzdrowiałaby. NNT wyliczane jest z wzoru:
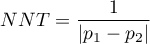
i jest cytowane wtedy, gdy różnica 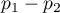 jest dodatnia.
jest dodatnia.
NNH (ang. number needed to harm)  wskaźnik stosowany w medycynie, oznacza liczbę pacjentów, których narażenie na ryzyko przez określony czas, powoduje uszczerbek na zdrowiu u jednej osoby, która w innych okolicznościach nie doznałaby uszczerbku. NNH wyliczane jest w ten sam sposób co NNT, ale jest cytowane wtedy, gdy różnica
wskaźnik stosowany w medycynie, oznacza liczbę pacjentów, których narażenie na ryzyko przez określony czas, powoduje uszczerbek na zdrowiu u jednej osoby, która w innych okolicznościach nie doznałaby uszczerbku. NNH wyliczane jest w ten sam sposób co NNT, ale jest cytowane wtedy, gdy różnica 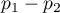 jest ujemna.
jest ujemna.
Przedział ufności  im węższy przedział ufności, tym bardziej precyzyjne oszacowanie. Jeśli w przedziale ufności zawarte jest 0 dla różnicy ryzyka, a
im węższy przedział ufności, tym bardziej precyzyjne oszacowanie. Jeśli w przedziale ufności zawarte jest 0 dla różnicy ryzyka, a 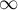 dla NNT i/lub NNH, to jest wskazanie do tego, by dany wynik traktować jako nieistotny statystycznie.
dla NNT i/lub NNH, to jest wskazanie do tego, by dany wynik traktować jako nieistotny statystycznie.
Uwaga!
Przedziały ufności dla różnicy dwóch niezależnych proporcji od wersji PQStat 1.3.0 estymowane są w oparciu o metodę Newcomba-Wilsona (Bender (2001)1), Newcombe (1998)2), Wilson (1927)3)). W poprzednich wersjach były estymowane w oparciu o metodę Walda.
Uzasadnienie zmiany:
Przedziały ufności oparte o klasyczną metodę Walda są odpowiednie dla dużych rozmiarów próbek i różnicy proporcji dalekiej od 0 lub 1. Dla małych prób i różnicy proporcji bliskiej tym skrajnym wartościom, w wielu sytuacjach praktycznych, metoda Walda może prowadzić do wyników niewiarygodnych (Newcombe 19984), Miettinen 19855), Beal 19876), Wallenstein 19977)). Porównanie i przeanalizowanie wielu metod, które mogą być używane zamiast prostej metody Walda, można znaleźć w pracy Newcombe (1998)8). Sugerowaną, odpowiednią również dla skrajnych wartości proporcji, jest roszerzona na przedziały dla różnicy dwóch niezależnych proporcji, metoda opublikowana po raz pierwszy przez Wilsona (1927)9).
Uwaga!
Przedział ufności dla NNT i/lub NNH wyliczany jest jako odwrotność przedziału dla proporcji, zgodnie ze sposobem zaproponowanym przez Altmana (Altman (1998)10)).
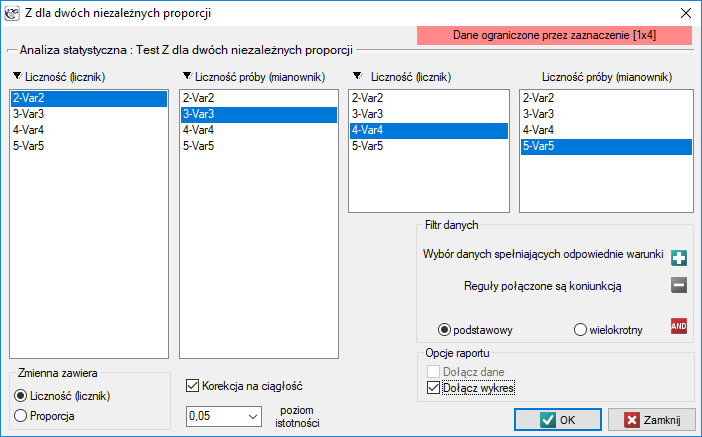
Okno z ustawieniami opcji testu Z dla dwóch niezależnych proporcji wywołujemy poprzez menu Statystyka→Testy nieparametryczne→Z dla dwóch niezależnych proporcji.
Przykład c.d. (plik płeć-egzamin.pqs)
Wiemy, że 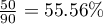 z wszystkich kobiet w próbie zdaje pozytywnie egzamin i
z wszystkich kobiet w próbie zdaje pozytywnie egzamin i 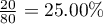 z wszystkich mężczyzn w próbie zdaje egzamin pozytywnie.
Dane możemy zapisać na dwa sposoby
z wszystkich mężczyzn w próbie zdaje egzamin pozytywnie.
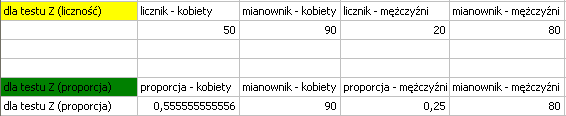
Dane możemy zapisać na dwa sposoby  jako licznik i mianownik dla każdej próby, lub jako proporcja i mianownik dla każdej próby:
jako licznik i mianownik dla każdej próby, lub jako proporcja i mianownik dla każdej próby:
Hipotezy:
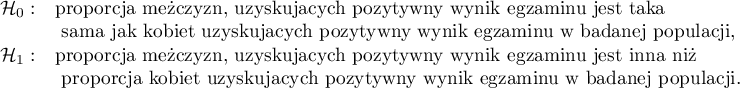
Uwaga!
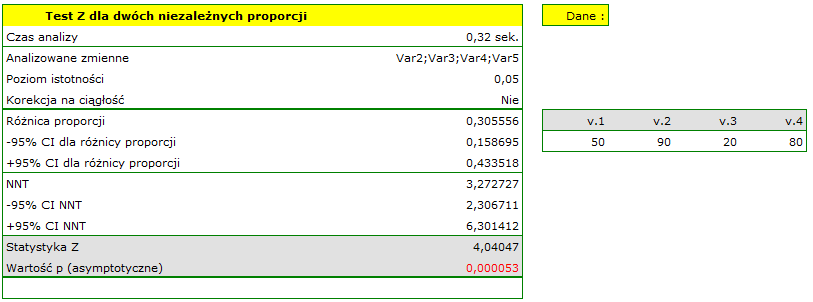
Ponieważ w arkuszu danych znajduje się więcej informacji, przed rozpoczęciem analizy należy zaznaczyć odpowiedni obszar (dane bez nagłówków). W oknie testu natomiast wybrać opcję mówiącą o zawartości zmiennej (liczność (licznik) lub proporcja).
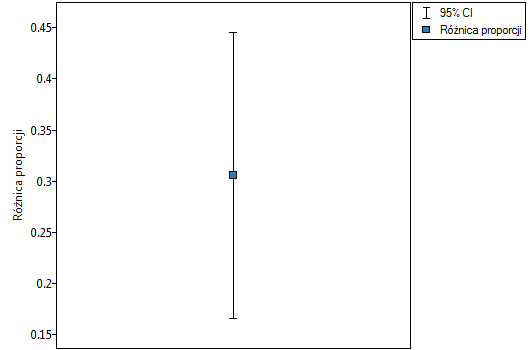
Różnica proporcji wyróżnionych w próbie to 30.56%, a 95% przedział ufności dla niej (15.90%, 43.35%) nie zawiera 0.
Na podstawie testu  bez poprawki na ciągłość (
bez poprawki na ciągłość ( =0.000053) jak też z poprawką na ciągłość (
=0.000053) jak też z poprawką na ciągłość ( =0.0001), na poziomie istotności
=0.0001), na poziomie istotności  =0.05 (podobnie jak w przypadku testu dokładnego Fishera, jego poprawki mid-p, testu
=0.05 (podobnie jak w przypadku testu dokładnego Fishera, jego poprawki mid-p, testu  i testu
i testu  z poprawką Yatesa) przyjmujemy hipotezę alternatywną. Zatem proporcja mężczyzn, uzyskujących pozytywny wynik egzaminu jest inna niż proporcja kobiet uzyskujących pozytywny wynik egzaminu w badanej populacji. Istotnie częściej ten egzamin zdają kobiety (
z poprawką Yatesa) przyjmujemy hipotezę alternatywną. Zatem proporcja mężczyzn, uzyskujących pozytywny wynik egzaminu jest inna niż proporcja kobiet uzyskujących pozytywny wynik egzaminu w badanej populacji. Istotnie częściej ten egzamin zdają kobiety (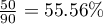 z wszystkich kobiet w próbie zdało egzamin) niż mężczyźni (
z wszystkich kobiet w próbie zdało egzamin) niż mężczyźni (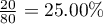 z wszystkich mężczyzn w próbie zdało egzamin).
z wszystkich mężczyzn w próbie zdało egzamin).
Przykład
Załóżmy, że choroba ma śmiertelność 100% bez leczenia, a terapia zmniejsza śmiertelność do 50% - jest to wynik 20 letnich badań. Chcemy wiedzieć jak wiele osób będzie trzeba leczyć, aby zapobiec w ciągu 20 lat 1 śmierci. By odpowiedzieć na to pytanie pobrano dwie 100 osobowe próby z populacji osób chorych. W próbie nieleczonych mamy 100 chorych pacjentów, wiemy, że bez leczenia wszyscy oni umrą. W próbie leczonych mamy również 100 pacjentów, z których 50 przeżyje.

Wyliczymy wskaźnik NNT.
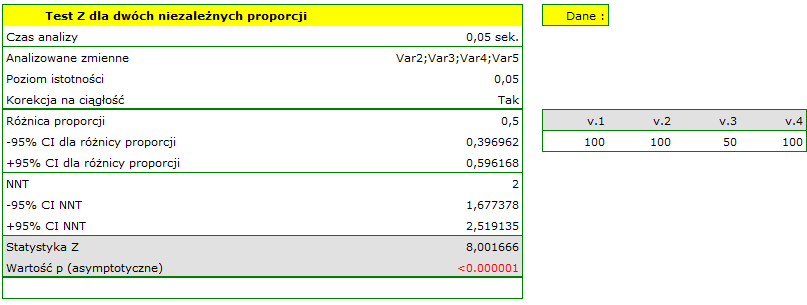
Różnica pomiędzy proporcjami jest istotna statystycznie (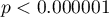 ), ale nas interesuje wskaźnik NNT - wynosi on 2, czyli stosowanie leczenia u 2 chorych przez 20 lat zapobiegnie 1 śmierci. Wyliczony 95% przedział ufności należy zaokrąglić do wartości całkowitych, co daje NNT od 2 do 3 chorych.
), ale nas interesuje wskaźnik NNT - wynosi on 2, czyli stosowanie leczenia u 2 chorych przez 20 lat zapobiegnie 1 śmierci. Wyliczony 95% przedział ufności należy zaokrąglić do wartości całkowitych, co daje NNT od 2 do 3 chorych.
Przykład
Wartość pewnej różnicy proporcji w badaniu porównującym skuteczność leku 1 vs lek 2 wynosiła różnica(95%CI)=-0.08 (-0.27 do 0.11). Ta ujemna różnica proporcji sugeruje, że lek 1 był mniej skuteczny niż lek 2, jego zastosowanie naraziło więc chorych na ryzyko. Ponieważ różnica proporcji jest ujemna, to wyznaczoną odwrotność nazywamy NNH, a ponieważ przedział ufności zawiera nieskończoność NNH(95%CI)= 2.5 (NNH 3.7 to ∞ to NNT 9.1) i przechodzi z NNH do NNT, należy uznać że uzyskany wynik nie jest istotny statystycznie (Altman (1998)11)).
1)
Bender R. (2001), Calculating confidence intervals for the number needed to treat. Controlled Clinical Trials 22:102–110
2)
, 4)
, 8)
Newcombe R.G. (1998), Interval Estimation for the Difference Between Independent Proportions: Comparison of Eleven Methods. Statistics in Medicine 17: 873-890
3)
, 9)
Wilson E.B. (1927), Probable Inference, the Law of Succession, and Statistical Inference. Journal of the American Statistical Association: 22(158):209-212
5)
Miettinen O.S. and Nurminen M. (1985), Comparative analysis of two rates. Statistics in Medicine 4: 213-226
6)
Beal S.L. (1987), Asymptotic confidence intervals for the difference between two binomial parameters for use with small samples. Biometrics 43: 941-950
7)
Wallenstein S. (1997), A non-iterative accurate asymptotic confidence interval for the difference between two Proportions. Statistics in Medicine 16: 1329-1336
statpqpl/porown2grpl/nparpl/z_nzalrpl.txt · ostatnio zmienione: 2022/01/23 21:18 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International


