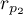Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:korelpl:parpl:rpbetaporpl
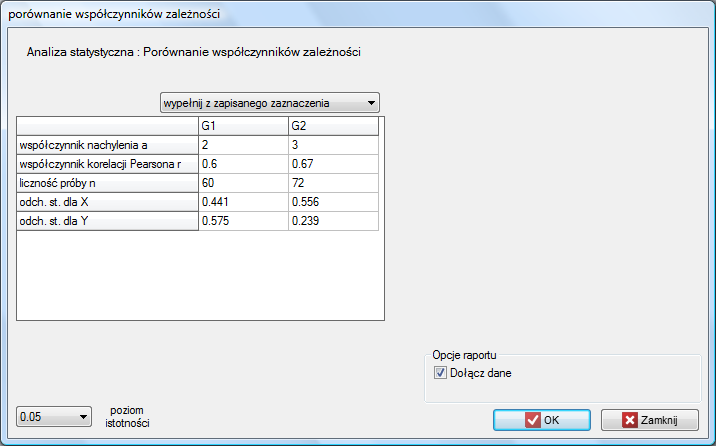
Porównanie nachylenia prostych regresji
Test t do sprawdzania równości współczynników regresji liniowej pochodzących z 2 niezależnych populacji
Test ten służy do weryfikacji hipotezy o równości dwóch współczynników regresji liniowej 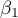 i
i 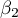 w badanych populacjach.
w badanych populacjach.
Podstawowe warunki stosowania:
- współczynniki
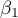 i
i 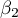 badają zależność tych samych cech
badają zależność tych samych cech  i
i  ,
, - znane są liczności obu prób
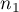 i
i 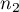 ,
,
Hipotezy:
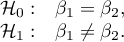
Statystyka testowa ma postać:
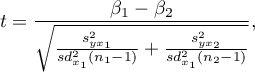
gdzie:
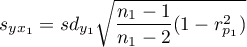 ,
,
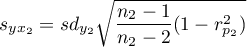 .
.
Statystyka testowa ma rozkład t-Studenta z 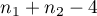 stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Okno z ustawieniami opcji porównania współczynników zależności wywołujemy poprzez menu Statystyka→Testy parametryczne→porównanie współczynników zależności.
statpqpl/korelpl/parpl/rpbetaporpl.txt · ostatnio zmienione: 2022/01/23 21:39 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

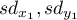 i
i 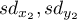 ,
,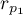 i
i