PQStat - Baza Wiedzy

Statystyka lokalna Getisa i Orda

Statystyka lokalna 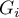$G_i$ Getisa i Orda (Getis i Ord 1992 Ordi Getis 1995) umożliwia wykrywanie lokalnej koncentracji wartości wysokich i niskich w sąsiadujących obiektach oraz bada istotność statystyczną tej zależności. Getis i Ord zdefiniował również bliźniaczą do 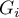$G_i$ statystykę 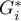$G^*_i$ , która różni się od 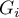$G_i$ jedynie tym, że obiekt dla którego wykonuje się badanie również bierze udział w analizie. W macierzy wag jest więc zdefiniowane dla niego sąsiedztwo z samym sobą tzw. potencjał (wartości na przekątnej są większe od 0).

Lokalny współczynnik autokorelacji Getisa i Orda

Lokalna postać współczynnika 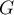$G$ Getisa i Orda dla obserwacji $i$ określona jest wzorem:

$\begin{displaymath} G_i=\frac{\sum_{j=1}^nw_{ij}x_j}{\sum_{j=1}^nx_j}, \quad \textrm{gdzie: $i\neq j$.} \end{displaymath}$

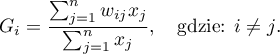
Współczynnik 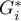$G^*_i$ zdefiniowany jest tym samym wzorem, lecz obliczenia przeprowadzane są również dla obiektu badanego czyli obiektu, dla którego indeksy $i$ oraz $j$ są sobie równe.

Ponieważ współczynnik bazuje na ilorazie dwóch sum wartości obiektów (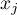 $x_j$ ), dla poprawnej interpretacji współczynnika ważne jest by analizowane zjawisko opisane było za pomocą liczb dodatnich. Interpretacja lokalnego współczynnika Getisa i Orda, podobnie jak lokalnego współczynnika Morana, w znacznym stopniu zależy od wybranej macierzy wag (zaleca się standaryzację macierzy rzędami do jedynki). 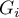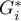Wysokie wartości współczynnika $G_i$ lub $G^*_i$ świadczą o skoncentrowaniu obiektów o wysokich wartościach analizowanego zjawiska, natomiast wartości niskie świadczą o skupisku obiektów o niskich wartościach. Gdy wartości są bliskie wartości oczekiwanej, wówczas rozkład badanej wartości w przestrzeni jest losowy.

Wartość oczekiwana określona jest wzorem:

$\begin{displaymath} E(G_i)=\frac{\sum_{j=1}^nw_{ij}}{n-1}, \quad \textrm{gdzie: $i\neq j$}; \end{displaymath}$

$\begin{displaymath} E(G_i^*)=\frac{\sum_{j=1}^nw_{ij}}{n}. \end{displaymath}$

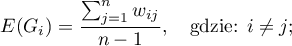
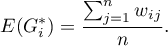
Istotność współczynnika Getisa i Orda

Testując istotność statystyczną związku między sąsiadującymi obiektami bada się hipotezy:

$\begin{array}{clccl} \mathcal{H}_0: & G_i = E(G_i) & \quad & \mathcal{H}_0: & G_i^* = E(G_i^*)\\ \mathcal{H}_1: & G_i \ne E(G_i), & \quad & \mathcal{H}_1: & G_i^* \ne E(G_i^*). \end{array}$

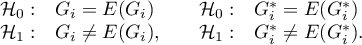
Statystyka testowa ma postać:

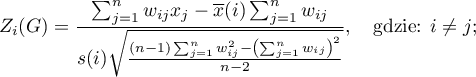
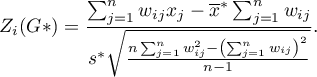
$\begin{displaymath} Z_i(G)=\frac{\sum_{j=1}^nw_{ij}x_j-\overline{x}(i)\sum_{j=1}^nw_{ij}}{s(i)\sqrt{\frac{(n-1)\sum_{j=1}^nw_{ij}^2-\left(\sum_{j=1}^nw_{ij}\right)^2}{n-2}}}, \quad \textrm{gdzie: 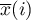$i\neq j$}; \end{displaymath}$ $\begin{displaymath} Z_i(G*)=\frac{\sum_{j=1}^nw_{ij}x_j-\overline{x}^*\sum_{j=1}^nw_{ij}}{s^*\sqrt{\frac{n\sum_{j=1}^nw_{ij}^2-\left(\sum_{j=1}^nw_{ij}\right)^2}{n-1}}}. \end{displaymath}$

gdzie:

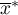$\overline{x}(i)$ i $\overline{x}^*$ - średnia zmiennej $X$ ,

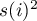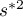$s(i)^2$ i $s^{*2}$ - wariancja zmiennej $X$ .

Statystyka 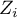$Z_i$ ma asymptotycznie (dla dużych liczności) rozkład normalny.

Wartość $p$ , wyznaczoną na podstawie statystyki testowej, porównujemy z poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

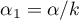Ze względu na problem braku niezależności współczynników wyliczanych dla sąsiednich obiektów sugeruje się stosowanie skorygowanego poziomu istotności $\alpha$ . Proponowane poprawki to: poprawka Bonferroniego: $\alpha_1=\alpha/k$ lub Sidaka: 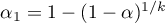$\alpha_1=1-(1-\alpha)^{1/k}$ , gdzie $k$ jest średnią liczbą sąsiadów.

Warstwy mapy

Kombinacja informacji z wielkości statystyki testowej 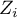$Z_i$ oraz jej istotności przedstawia na mapie tzw. reżimy przestrzenne:

Istotne statystycznie obiekty o wysokich wartościach statystyki 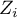$Z_i$ oznaczone są jako High-High (obiekty o wysokich wartościach otoczone przez obiekty o wysokich wartościach) i zaznaczone na mapie kolorem czerwonym;

Istotne statystycznie obiekty o niskich wartościach statystyki 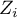$Z_i$ oznaczone są jako Low-Low (obiekty o niskich wartościach otoczone przez obiekty o niskich wartościach) i zaznaczone na mapie kolorem niebieskim.

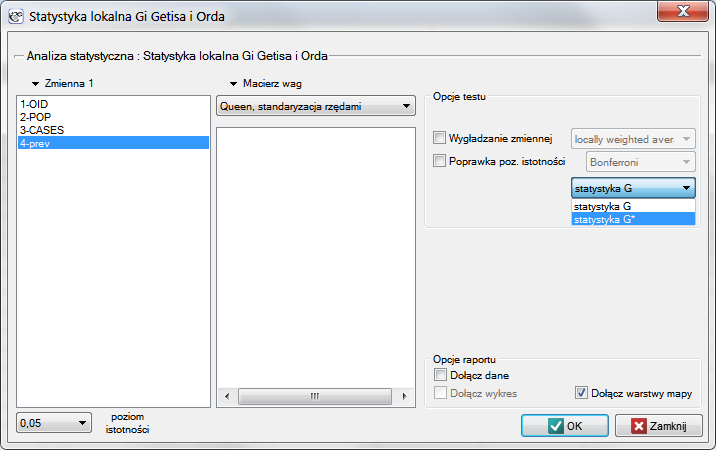
Okno z ustawieniami opcji lokalnej analizy Getisa i Orda wywołujemy poprzez menu Analiza przestrzenna → Statystyki przestrzenne → Statystyka lokalna <latex>$G_i$</latex> Getisa i Orda.

Przykład c.d. (katalog: leukemia, plik: leukemia)

Analizie poddamy dane dotyczące białaczki.

Mapa leukemia zawiera informacje o lokalizacji 281 wielokątów (regionów spisowych (ang.census tracts)) w północnej części stanu New York.
Dane do mapy leukemia:
- Kolumna CASES – liczba przypadków białaczki w latach 1978-1982 przypisana do poszczególnych obiektów (regionów spisowych). Wartość ta powinna być liczbą całkowitą, tu jednak, zgodnie z opisem Wallera (1994) część przypadków, która nie mogła zostać obiektywnie przypisana do konkretnego regionu, została podzielona proporcjonalnie. Stąd liczności przypadków przypisanych do 281 obiektów nie są liczbami całkowitymi.
- Kolumna POP – liczność populacji w poszczególnych obiektach.
- Kolumna prev – współczynnik częstości występowania białaczki na 100000 osób, dla każdego obiektu w jednym roku: prev=(CASES/POP)*100000/5

Analiza globalna nie dała jednoznacznego rozstrzygnięcia co do występowania autokorelacji przestrzennej. Sprawdzimy więc, czy uda się znaleźć regiony, gdzie częstość występowania białaczki jest nieprzeciętnie wyższa.

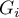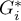By zlokalizować skupiska białaczki wyliczymy współczynnik $G_i$ oraz $G_i^*$ . Do analizy wykorzystamy zmienną prev oraz proponowaną przez program macierz sąsiedztwa według wspólnej granicy – Queen, standaryzowaną rzędami (by wykorzystać inną macierz należy ją najpierw wygenerować - patrz rozdział: Macierz wag przestrzennych). Wybieramy również jedną z poprawek poziomu istotności.

Uzyskany raport przedstawia wartości lokalnych współczynników, wartości statystyki testowej oraz odpowiadające im wartości prawdopodobieństwa testowego. Znajdziemy tu również informacje o ilości rejonów wyznaczających reżimy przestrzenne (High-High, Low-Low).

Do analizy przypisany jest także wynik, który możemy wyrysować na mapie (przycisk ) - są to reżimy przestrzenne opisane w raporcie poprzez kolumnę kolor.

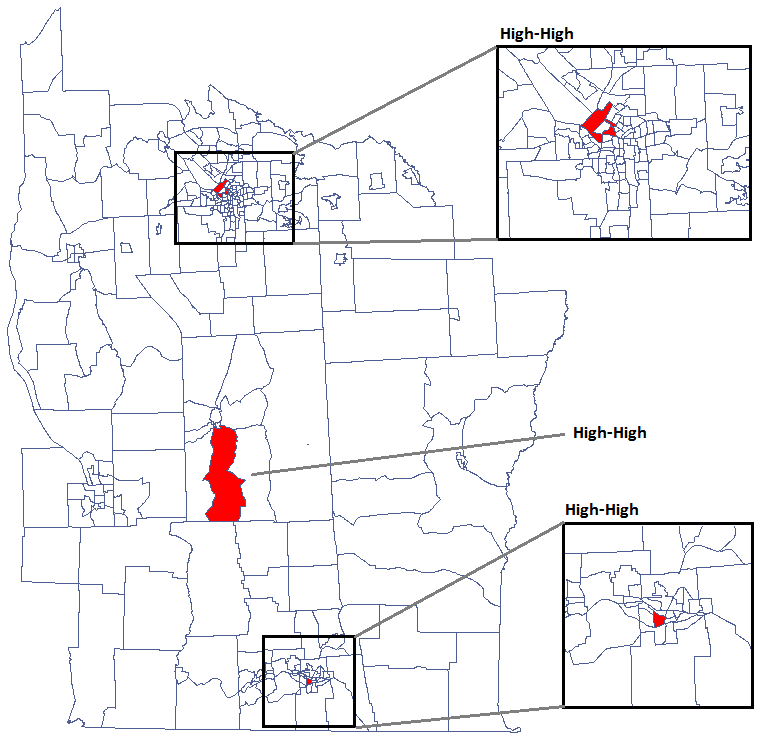
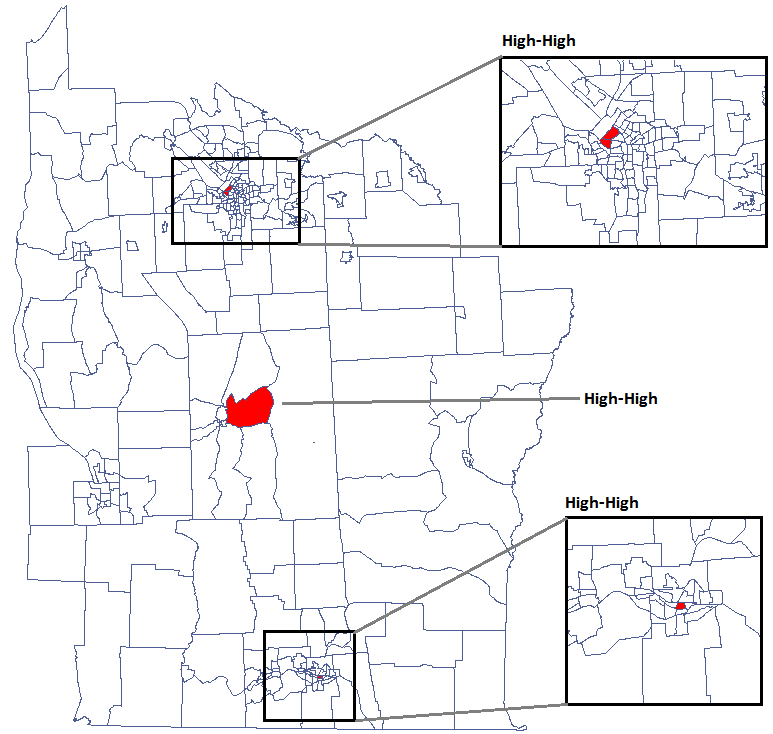
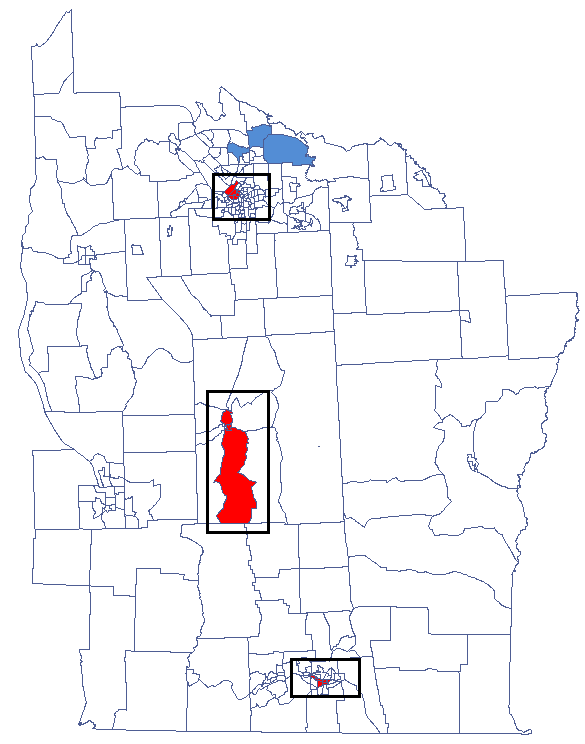
Udało się zlokalizować 3 skupiska (6 regionów spisowych w analizie współczynnika 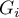$G_i$ i 4 regiony w analizie współczynnika 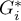$G_i^*$ ) gdzie częstość występowania białaczki jest istotnie wyższa. Są to centra klasterów wysokich wartości białaczki oznaczone na mapie kolorem czerwonym.

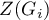Uzyskane wyniki możemy dodatkowo zobrazować kolorując mapę wartościami lokalnego współczynnika Getisa i Orda lub też wartościami statystyki testowej bądź wartościami $p$ . Wystarczy jedynie wcześniej przekopiować odpowiednie kolumny z raportu do arkusza danych. W tym przykładzie do kolorowania wykorzystamy wartości statystyki testowej $Z(G_i)$ . Po wklejeniu jej do pustej kolumny arkusza danych, w menadżerze map kolorujemy mapę bazową zgodnie z wartościami tej kolumny wybierając odchylenie standardowe o współczynniku 3 jako sposób gradacji kolorów. Dodatnie i wysokie wartości statystyki 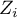$Z_i$ świadczą o skoncentrowaniu obiektów o wysokich wartościach, wartości ujemne i niskie - obiektów o niskich wartościach, a wartości bliskie zeru wskazują na losowy rozkład badanej zmiennej w przestrzeni.

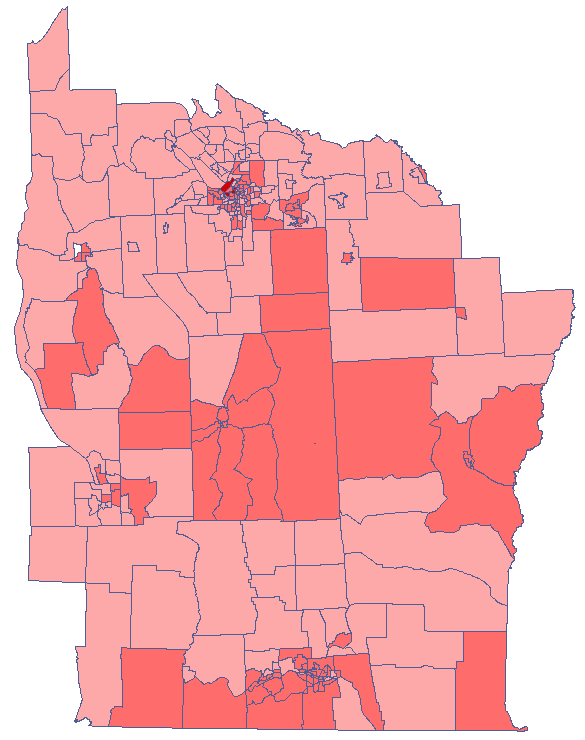
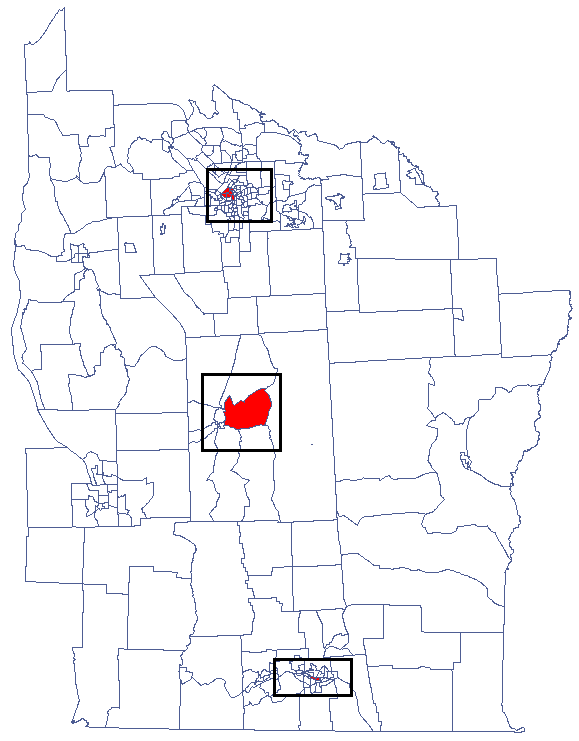
Analizując wygładzoną zmienną prev wzmacniamy efekt klasteryzacji. Uzyskujemy podobny rezultat, czyli 3 skupiska (15 regionów spisowych w analizie współczynnika 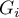$G_i$ i 9 regionów w analizie współczynnika $G_i^*$ ) będące centrami klasterów.

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Statystyka lokalna Getisa i Orda

Narzędzia strony