Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
en:statpqpl:korelpl:parpl:rpistpl
The Pearson correlation coefficient significance
The test of significance for Pearson product-moment correlation coefficient is used to verify the hypothesis determining the lack of linear correlation between an analysed features of a population and it is based on the Pearson's linear correlation coefficient calculated for the sample. The closer to 0 the value of coefficient 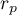 is, the weaker dependence joins the analysed features.
is, the weaker dependence joins the analysed features.
Basic assumptions:
- measurement on the interval scale,
- normality of distribution of residuals or an analysed features in a population.
Hypotheses:
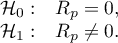
The test statistic is defined by:
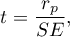
where 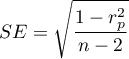 .
.
The value of the test statistic can not be calculated when 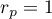 or
or 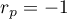 or when
or when 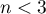 .
.
The test statistic has the t-Student distribution with 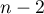 degrees of freedom.
degrees of freedom.
The p-value, designated on the basis of the test statistic, is compared with the significance level  :
:
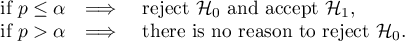
EXAMPLE cont. (age-height.pqs file)
en/statpqpl/korelpl/parpl/rpistpl.txt · ostatnio zmienione: 2022/02/13 18:45 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

