PQStat - Baza Wiedzy

Analiza reszt modelu

By otrzymać poprawny model regresji, powinniśmy sprawdzić podstawowe założenia dotyczące reszt modelu.

Obserwacje odstające

Badając reszty modelu szybko można uzyskać wiedzę na temat wartości odstających. Obserwacje takie mogą bardzo zaburzyć równanie regresji, ponieważ mają duży wpływ na wartości współczynników tego równania. Jeśli dana reszta 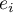$e_i$ jest oddalona o więcej niż 3 odchylenia standardowe od wartości średniej, wówczas obserwacje taką można uznać za obserwacje odstającą. Usunięcie obserwacji odstającej może w znaczącym stopniu przyczynić się do poprawy modelu.

Odległość Cooka - opisuje wielkość zmian współczynników regresji powstałą na skutek pominięcia danego przypadku. W programie zaznaczone pogrubioną czcionką są odległości Cooka dla przypadków, które przekraczają 50 percentyl statystyki rozkładu Fishera-Snedecora F(0.5, k+1, n−k−1).

Odległość Mahalanobisa - dedykowana jest do wykrywania obserwacji odstających - wysokie wartości świadczą o znacznym oddaleniu danego przypadku od centrum zmiennych niezależnych. Jeśli wśród przypadków oddalonych o więcej niż 3 odchylenia znajdzie się przypadek o największej wartości Mahalanobisa, wówczas jako najbardziej odstający zostanie on zaznaczony pogrubioną czcionką.

Normalność rozkładu reszt modelu

Założenie to sprawdzamy wizualnie przy pomocy wykresu Q-Q rozkładu nromalnego. Duża różnica między rozkładem reszt a rozkładem normalnym może zaburzać ocenę istotności współczynników poszczególnych zmiennych modelu..

Homoskedastyczność (stałość wariancji)

By sprawdzić czy istnieją obszary, gdzie wariancja reszt modelu jest zwiększona lub zmniejszona posługujemy się wykresami:

reszty względem wartości przewidywanych
kwadrat reszty względem wartości przewidywanych
reszty względem wartości obserwowanych
kwadrat reszty względem wartości obserwowanych

Autokorelacja reszt modelu

Aby zbudowany model można było uznać za poprawny, wartości reszt nie powinny być ze sobą skorelowane (dla wszystkich par 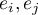$e_i, e_j$ ). Założenie to możemy sprawdzić wyliczając statystykę testu Durbina-Watsona

$\begin{displaymath} d=\frac{\sum_{t=2}^n\left(e_t-e_{t-1}\right)^2}{\sum_{t=1}^ne_t^2}, \end{displaymath}$

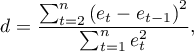
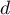Aby sprawdzić dodatnią autokorelację na poziomie istotności $\alpha$ , sprawdzamy położenie statystyki $d$ w stosunku do górnej ( 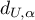$d_{U,\alpha}$ ) i dolnej ( 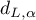$d_{L,\alpha}$ ) wartości krytycznej:

Jeżeli 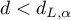$d <d_{L,\alpha}$ - błędy są dodatnio skorelowane;
Jeśli 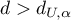$d> d_{U,\alpha}$ - błędy nie są dodatnio skorelowane;
Jeśli 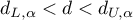$d_{L,\alpha}<d <d_{U,\alpha}$ - wynik testu jest niejednoznaczny.

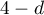Aby sprawdzić ujemną autokorelację na poziomie istotności $\alpha$ , sprawdzamy położenie wartości $4-d$ w stosunku do górnej ( 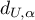$d_{U,\alpha}$ ) i dolnej ( 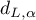$d_{L,\alpha}$ ) wartości krytycznej:

Jeżeli 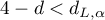$4-d <d_{L,\alpha}$ - błędy są ujemnie skorelowane;
Jeśli 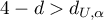$4-d> d_{U,\alpha}$ - błędy nie są ujemnie skorelowane;
Jeśli $d_{L,\alpha}<4-d <d_{U,\alpha}$ - wynik testu jest niejednoznaczny.

Wartości krytyczne testu Durbina-Watsona dla poziomu istotności $\alpha=0.05$ znajdują się na stronie internetowej (pqstat) - źródło tablic: Savina i White (1977)¹⁾

Przykład c.d. (plik wydawca.pqs)

¹⁾

Savin N.E. and White K.J. (1977), The Durbin-Watson Test for Serial Correlation with Extreme Sample Sizes or Many Regressors. Econometrica 45, 1989-1996

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Analiza reszt modelu

Narzędzia strony