PQStat - Baza Wiedzy

Porównywanie modeli liniowej regresji wielorakiej

Okno z ustawieniami opcji porównywania modeli wywołujemy poprzez menu Statystyka→Modele wielowymiarowe→Regresja wieloraka - porównywanie modeli

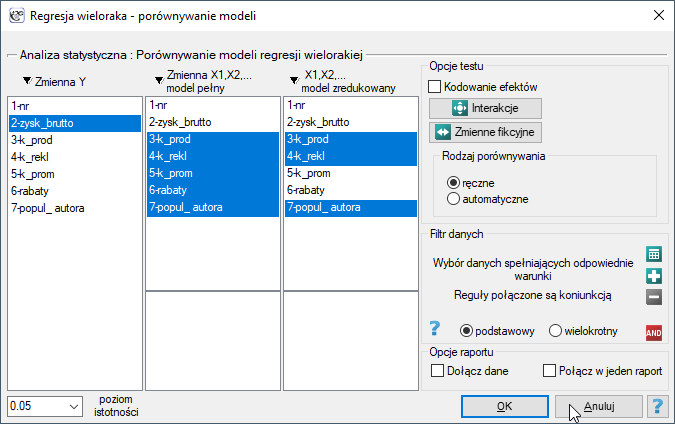
Liniowa regresja wieloraka daje możliwość jednoczesnej analizy wielu zmiennych niezależnych. Pojawia się więc problem wyboru optymalnego modelu. W natłoku informacji jakie niesie zbyt duży model istnieje możliwość zagubienia ważnych informacji. Zbyt mały może pominąć te cechy, które w wiarygodny sposób mogłyby opisać badane zjawisko. Bowiem nie liczba zmiennych w modelu, ale ich jakość decyduje o jakości modelu. W wyborze zmiennych niezależnych niezbędna jest wiedza i doświadczenie związane z badanym zjawiskiem. Należy pamiętać, by w modelu znajdowały się zmienne silnie skorelowane ze zmienną zależną i słabo skorelowane między sobą.

Nie istnieje jedna prosta reguła statystyczna, która decydowałaby o liczbie zmiennych niezbędnych w modelu. Najczęściej w porównaniu posługujemy się miarami dopasowania modelu takimi jak: 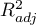$R_{adj}^2$ - poprawiona wartość współczynnika determinacji wielorakiej (im wyższa wartość tym lepiej dopasowany model), 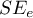$SE_e$ - błąd standardowy estymacji (im niższa wartość tym lepiej dopasowany model) lub kryteria informacyjne AIC, AICc, BIC (im niższa wartość tym lepszy model). W tym celu można również wykorzystać test F oparty o współczynnik determinacji wielorakiej $R^2$ . Test ten służy do weryfikacji hipotezy, że dopasowanie obu porównywanych modeli jest tak samo dobre.

Hipotezy:

$\begin{array}{cc} \mathcal{H}_0: & R_{FM}^2=R_{RM}^2,\\ \mathcal{H}_1: & R_{FM}^2\ne R_{RM}^2, \end{array}$

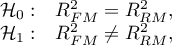
gdzie:

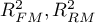
$R_{FM}^2, R_{RM}^2$ $-$ współczynniki determinacji wielorakiej w porównywanych modelach (pełnym i zredukowanym).

Statystyka testowa ma postać:

$\begin{displaymath} F=\frac{R_{FM}^2-R_{RM}^2}{k_{FM}-k_{RM}}\cdot\frac{n-k_{FM}-1}{1-R_{FM}^2}, \end{displaymath}$

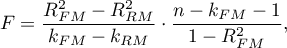
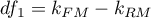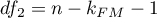Statystyka ta podlega rozkładowi F Snedecora z $df_1=k_{FM}-k_{RM}$ i $df_2=n-k_{FM}-1$ stopniami swobody.

Wyznaczoną na podstawie statystyki testowej wartość $p$ porównujemy z poziomem istotności $\alpha$ :

$\begin{array}{ccl} $ jeżeli $ p \le \alpha & \Longrightarrow & $ odrzucamy $ \mathcal{H}_0 $ przyjmując $ \mathcal{H}_1, \\ $ jeżeli $ p > \alpha & \Longrightarrow & $ nie ma podstaw, aby odrzucić $ \mathcal{H}_0. \\ \end{array}$

Jeśli porównywane modele nie różnią się istotnie, to powinniśmy wybrać ten z mniejszą liczbą zmiennych. Brak różnicy oznacza bowiem, że zmienne które są w modelu pełnym, a nie ma ich w modelu zredukowanym, nie wnoszą istotnej informacji. Jeśli natomiast różnica w jakości dopasowania modeli jest istotna statystycznie oznacza to, że jeden z nich (ten z większą liczbą zmiennych, o większym $R^2$ lub mniejszej wielkości kryterium informacyjnego) jest istotnie lepszy niż drugi.

W programie PQStat porównywanie modeli możemy przeprowadzić ręcznie lub automatycznie.

Ręczne porównywanie modeli- polega na zbudowaniu 2 modeli:

pełnego - modelu z większą liczbą zmiennych,

zredukowanego - modelu z mniejszą liczbą zmiennych $-$ model taki powstaje z modelu pełnego po usunięciu zmiennych, które z punktu widzenia badanego zjawiska są zbędne.

Wybór zmiennych niezależnych w porównywanych modelach a następnie wybór lepszego modelu, na podstawie uzyskanych wyników porównania, należy do badacza.

Automatyczne porównywanie modeli jest wykonywane w kilku krokach:

[krok 1] Zbudowanie modelu z wszystkich zmiennych.

[krok 2] Usunięcie jednej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.

[krok 3] Porównanie modelu pełnego i zredukowanego.

[krok 4] Usunięcie kolejnej zmiennej z modelu. Usuwana zmienna to ta, która ze statystycznego punktu widzenia wnosi do aktualnego modelu najmniej informacji.

[krok 5] Porównanie modelu wcześniejszego i nowo zredukowanego.

[…]

W ten sposób powstaje wiele, coraz mniejszych modeli. Ostatni model zawiera tylko 1 zmienną niezależną.

W rezultacie, każdy model jest opisany miarami dopasowania (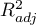 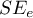$R_{adj}^2$ , $SE_e$ , AIC, AICc, BIC), a kolejno powstające (sąsiednie) modele są porównywane testem F. Model, który zostanie ostatecznie zaznaczony jako statystycznie optymalny, to model o największym 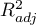$R_{adj}^2$ , najmniejszym kryterium informacyjnym i najmniejszym 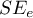$SE_e$ . Ponieważ jednak żadna z metod statystycznych nie potrafi w pełni odpowiedzieć na pytanie który z modeli jest najlepszy, to badacz, na podstawie uzyskanych wyników, powinien wybrać model.

Przykład c.d. (plik wydawca.pqs)

Do przewidywania zysku brutto ze sprzedaży książek wydawca planuje brać pod uwagę takie zmienne jak: koszty produkcji, koszty reklamy, koszty promocji bezpośredniej, suma udzielonych rabatów, popularność autora. Nie wszystkie te zmienne muszą jednak wpływać znacząco na zysk. Spróbujemy wybrać taki model regresji liniowej, który będzie zawierał optymalną (ze statystycznego punktu widzenia) liczbę zmiennych. Do tej analizy użyjemy danych zbioru uczącego.

Ręczne porównywanie modeli.

Na podstawie zbudowanego wcześniej modelu pełnego możemy podejrzewać, że zmienne: koszty promocji bezpośredniej, suma udzielonych rabatów mają niewielki wpływ na budowany model (tzn. te zmienne nie pomagają przewidzieć wielkości zysku). Sprawdzimy czy, ze statystycznego punktu widzenia, model pełny jest lepszy niż model po usunięciu tych dwóch zmiennych.

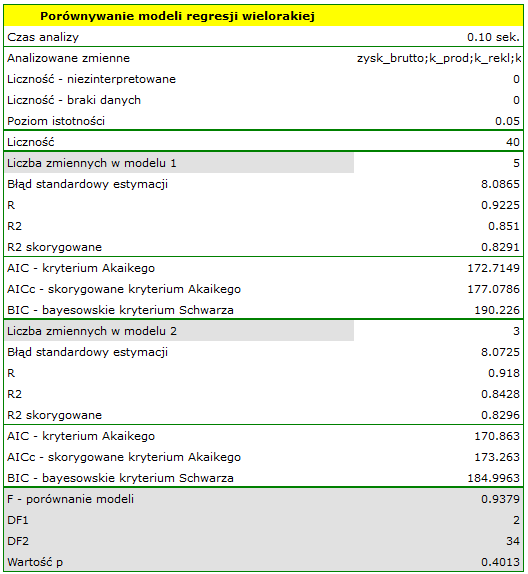
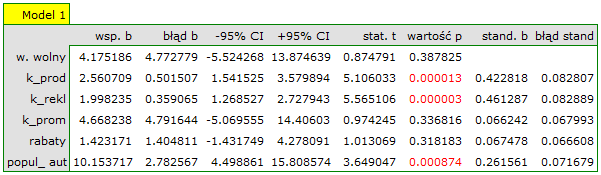
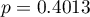Okazuje się, że nie ma podstaw by uważać, że model pełny jest lepszy niż model zredukowany (wartość $p$ testu F służącego porównywaniu modeli wynosi $p=0.4013$ ). Dodatkowo, model zredukowany jest nieco lepiej dopasowany niż model pełny (dla modelu zredukowanego 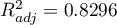$R_{adj}^2=0.8296$ , dla modelu pełnego 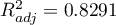$R_{adj}^2=0.8291$ ) oraz ma mniejsze, czyli korzystniejsze wartości kryteriów informacyjnych AIC, AICc i BIC.

Automatyczne porównywanie modeli.

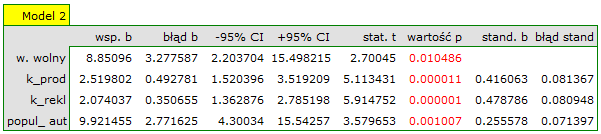
W przypadku automatycznego porównywania modeli uzyskaliśmy bardzo podobne wyniki. Najlepszym modelem jest model o największym współczynniku 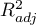$R^2_{adj}$ , najmniejszych kryteriach informacyjnych i najmniejszym błędzie standardowym estymacji 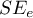$SE_e$ . Sugerowanym najlepszym modelem jest tu model zawierający tylko 3 zmienne niezależne: koszty produkcji, koszty reklamy, popularność autora. Na podstawie powyższych analiz, ze statystycznego punktu widzenia, optymalnym modelem jest model zawierający 3 najważniejsze zmienne niezależne: koszty produkcji, koszty reklamy, popularność autora. Jednak ostateczna decyzja, który model wybrać należy do osoby posiadającą specjalistyczną widzę z zakresu badania - w tym przypadku wydawcy. Należy pamiętać, że wybrany model powinien zostać ponownie zbudowany a jego założenia zweryfikowane w oknie Regresja wieloraka.

PQStat - Baza Wiedzy

Narzędzia użytkownika

Narzędzia witryny

Pasek boczny

Porównywanie modeli liniowej regresji wielorakiej

Narzędzia strony