Narzędzia użytkownika
Narzędzia witryny
Pasek boczny
statpqpl:norm:normmultipl
Testy normalności wielowymiarowej
Wiele metod analizy wielowymiarowej, w tym MANOVA, testy Hotellinga czy też modele regresji opierają się na założeniu normalności wielowymiarowej. Jeśli zbiór zmiennych charakteryzuje wielowymiarowy rozkład normalny, to można założyć, że każda zmienna posiada rozkład normalny. Jednak gdy wszystkie pojedyncze zmienne charakteryzowane są rozkładem normalnym, ich zestaw nie musi mieć wielowymiarowego rozkładu normalnego. Dlatego testowanie jednowymiarowej normalności każdej zmiennej może być przydatne, ale nie można założyć, że jest wystarczające.
Różne typy analiz statystycznych zakładające normalność są w różnym stopniu wrażliwe na różne rodzaje odejścia od tego założenia. Przyjmuje się, że testy odnoszące się w swoich hipotezach do średnich są bardziej wrażliwe na skośność, a testy porównujące kowariancje w większym stopniu zależą od kurtozy.
Okno z ustawieniami opcji testu wielowymiarowej normalności rozkładu wywołujemy poprzez menu Statystyka→Testy normalności→Normalność wielowymiarowa.
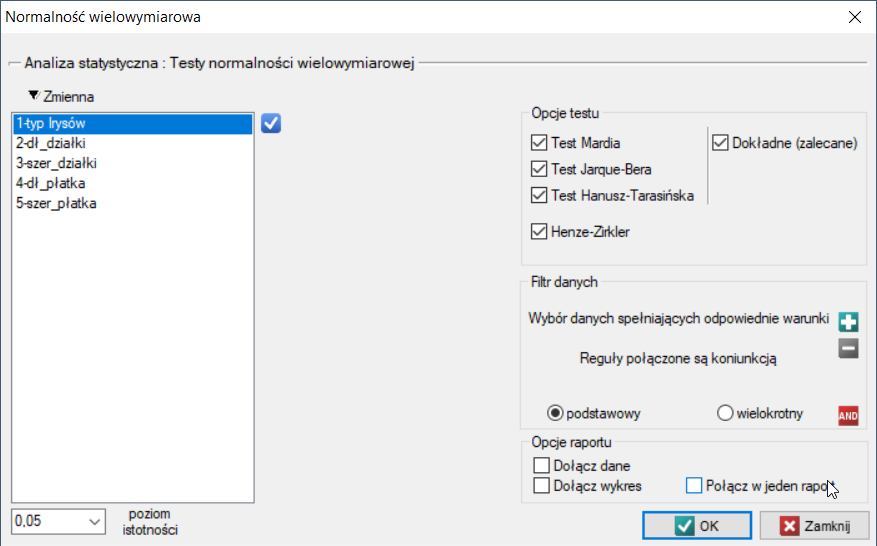
Test Mardia dla wielowymiarowej normalności rozkładu (ang. Mardia's test for multivariate normality)
Test zaproponowany przez Mardia w roku 1970 1) i zmodyfikowany w roku 1974 2) bada normalność rozkładu analizując oddzielnie rozmiar wielowymiarowej skośności i wielowymiarowej kurtozy. Jarque i Bera 3) zaproponowali złączenie tych dwóch miar Mardia w jeden test. Podobny sposób łączenia w jeden test informacji o skośności i kurtozie oferuje metoda Hanusz i Tarasińskiej 4).
Mardia zdefiniował wielowymiarową skośność i kurtozę następująco:
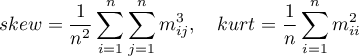 gdzie
gdzie
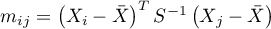 ,
,
 ,
,
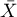 -średnia,
-średnia, 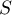 - macierz kowariancji.
- macierz kowariancji.
Dla danych pochodzących z próby, a nie z populacji wzory na skośność i kurtozę są mnożone odpowiednio: skośność przez 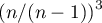 i kurtoza przez
i kurtoza przez 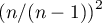 .
.
Hipotezy:
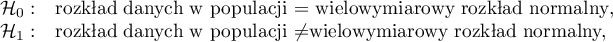
- Mardia test skośności:
Gdy próba pochodzi z populacji o wielowymiarowym rozkładzie normalnym (hipoteza zerowa), to statystyka testowa ma postać (Mardia, 1970):
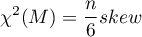
lub z poprawką dokładnych momentów dla grup o mniejszych licznościach (<20) (Mardia, 1974):
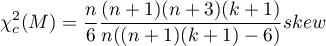
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 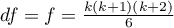 stopniami swobody.
stopniami swobody.
- Mardia test kurtozy:
Gdy próba pochodzi z populacji o wielowymiarowym rozkładzie normalnym (hipoteza zerowa), to statystyka testowa ma postać (Mardia, 1974):
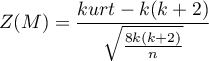
lub z poprawką (Mardia, 1974):
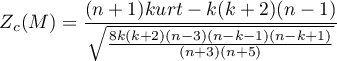
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład normalny.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Test Jarque-Bera dla wielowymiarowej normalności rozkładu (ang. Jarque-Bera test for multivariate normality)
Test Jarque i Bera (1987) 5) bazuje na statystyce skośności i kurtozy testu Mardia. Statystyka testowa ma postać:
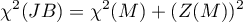
lub z poprawką (Mardia, 1974):
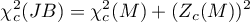
Statystyka ta ma asymptotycznie (dla dużych liczności) rozkład chi-kwadrat z 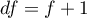 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Test Hanusz-Tarasińska dla wielowymiarowej normalności rozkładu (ang. Hanusz-Tarasinska test for multivariate normality)
Test Zofii Hanusz i Joanny Tarasińskiej (2014) 6) bazuje na statystyce skośności i kurtozy testu Mardia. Statystyka testowa ma postać:
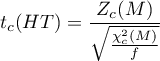
Statystyka testowa ma rozkład t-Studenta z 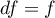 stopniami swobody.
stopniami swobody.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Test Henze-Zirklera dla wielowymiarowej normalności rozkładu (ang. Henze-Zirkler test for multivariate normality)
Henze i Zirklera (1990) 7) zaproponowali test badający wielowymiarową normalność rozkładu rozszerzając pracę Baringhausa i Henzego nad empiryczną funkcją charakterystyczną 8). W literaturze jest to test uznawany za jeden z najsilniejszych testów poświęconych wielowymiarowemu rozkładowi normalnemu (Thode 2002) 9). Statystyka testowa ma postać:
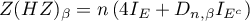
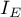 oraz
oraz 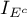 to funkcje indykatorowe zależne od osobliwości macierzy kowariancji,
to funkcje indykatorowe zależne od osobliwości macierzy kowariancji,
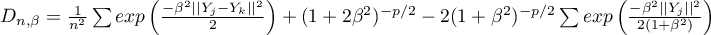
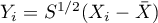
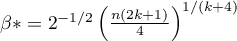 - optymalna wartość parametru
- optymalna wartość parametru 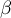
Statystyka 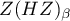 ma asymptotycznie (dla dużych liczności) rozkład normalny oparty na średniej i wariancji opisanej przez Henze i Zirklera i odczytywany jednostronnie.
ma asymptotycznie (dla dużych liczności) rozkład normalny oparty na średniej i wariancji opisanej przez Henze i Zirklera i odczytywany jednostronnie.
Wyznaczoną na podstawie statystyki testowej wartość  porównujemy z poziomem istotności
porównujemy z poziomem istotności  :
:

Przykład (plik Irysy.pqs)
Badamy normalność rozkładu dla klasycznego zestawu danych R.A. Fishera 1936 10). Plik znajduje się w pomocy dołączonej do programu i zawiera pomiary długości i szerokości płatków i działek kielicha dla 3 odmian kwiatu irysa. Analiza zostanie przeprowadzona oddzielnie dla każdej odmiany.
W oknie analizy zaznaczamy wszystkie testy oraz wykres, a w celu powtórzenia analizy dla każdej odmiany irysa ustawiamy filtr wielokrotny. Wszystkie wyniki zwrócimy do tego samego arkusza, dlatego zaznaczamy opcję Połącz w jeden raport.
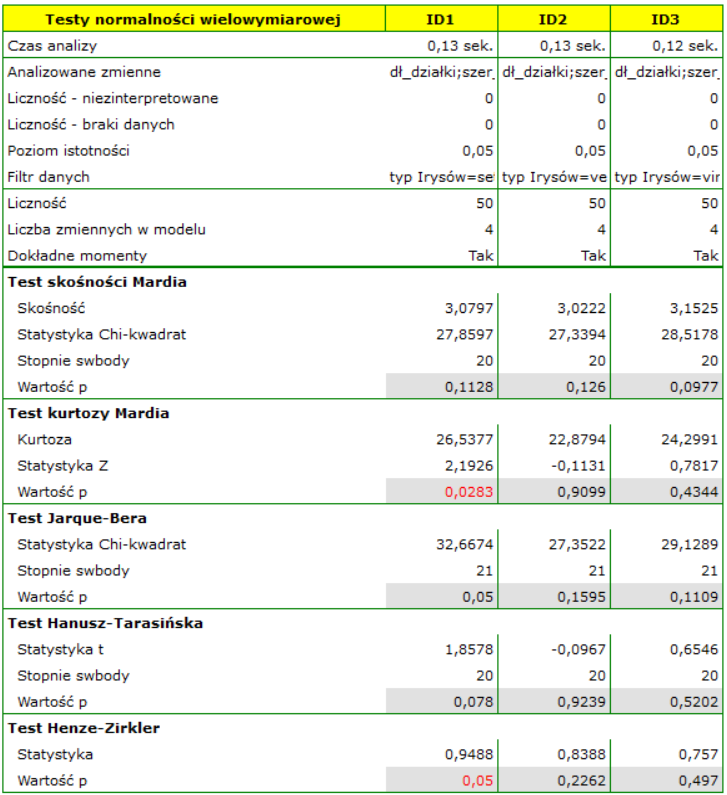
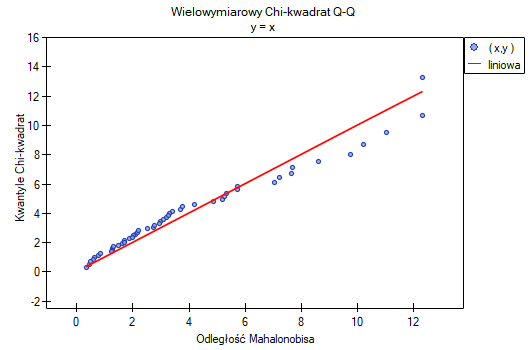
Wszystkie tety potwierdzają normalność rozkładu dla odmiany versicolor i virginica. W przypadku odmiany setosa wyniki testów są na pograniczu istotności statystycznej, przy czym test Mardia dla Kurtozy i test Henze-Zirkler wskazują na odstępstwa od wielowymiarowego rozkładu normalnego. Możemy obserwować takie odstępstwa również na pierwszym wykresie, gdzie wraz narastaniem odległości Mahalanobisa punkty znajdują się coraz dalej od prostej.
1)
Mardia K. V. (1970), Measures of multivariate skewness and kurtosis with applications, Biometrica 57, 519-530
2)
Mardia K. V. (1974), Applications of some measuresof multivariate skewness and kurtosis for testing normality and robustness studies, Sankhay B 36, 115-128
3)
, 5)
Jarque C. M., Bera A. K., (1987)., A test for normality of Observations and Regression Residuals, International Statistical Review 55, 163-172
4)
, 6)
Hanusz Z., Tarasińska J. (2014), On multivariate normality tests using skewness and kurtosis, Colloquium Biometricum 44, 139-148
7)
Henze N., Zirkler B. (1990), A class of invariant consistent tests for multivariate normality. Comm. Statist. Theory Methods. 1990;19:3595–3617
8)
Epps T.W., Pulley L.B. (1983), A test for normality based on the empirical characteristic function. Biometrika. 1983;70:723–726
9)
Thode H. C. (2002), Testing For Normality. CRC Press; 2002. 506 s.
10)
Fisher R.A. (1936), The use of multiple measurements in taxonomic problems. Annals of Eugenics 7 (2): 179–188
statpqpl/norm/normmultipl.txt · ostatnio zmienione: 2022/02/11 20:07 przez admin
Narzędzia strony
Wszystkie treści w tym wiki, którym nie przyporządkowano licencji, podlegają licencji: CC Attribution-Noncommercial-Share Alike 4.0 International

